Привет.
Встав сегодня утром с кровати, я думал о том, как написать статью на Хабр о фазовых портретах, и первым делом стоило посмотреть писал ли кто об этом чудесном методе. Как оказалось нет. ОСТОРОЖНО, под катом трафик.
Для лучшего усваивания материала предлагаю включить Bob Acri – Guess Who.
Ну, пожалуй, начнем.
Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём одной единственной точкой, а эволюция этой системы — перемещением этой точки.
След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных сочетаний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц.
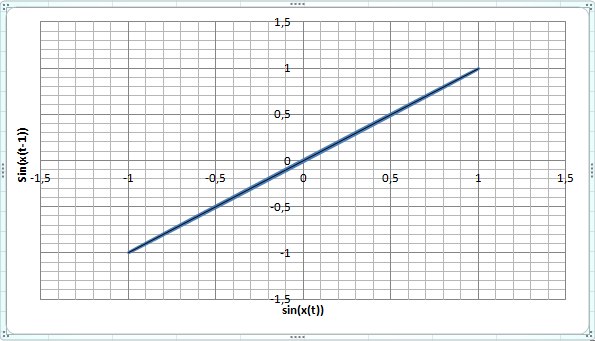
Не буду скрывать, что этот метод анализа пришел в IT из физики, но как только вы его увидите, вы сразу его полюбите. Этот метод гораздо быстрее чем метод преобразования Фурье. И особенно хорош при исследовании данных в реальном времени. Т.е. просто нужно построить график где будет отображаться зависимость текущего параметра от предыдущего, и вот он фазовый портрет. Построим, например, для sin(x):
Наглядно, как строить:
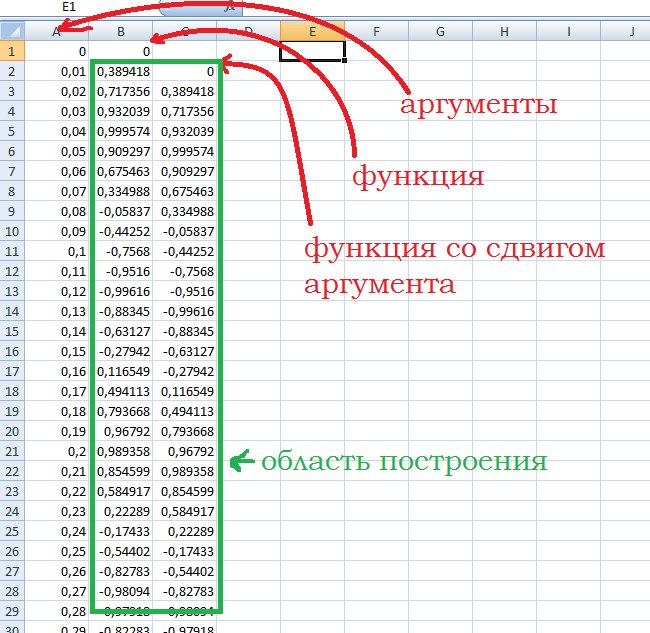
Не хотелось расчехлять давно зачехленный Matlab, по этому использовал первое, что пришло на ум — Exel.
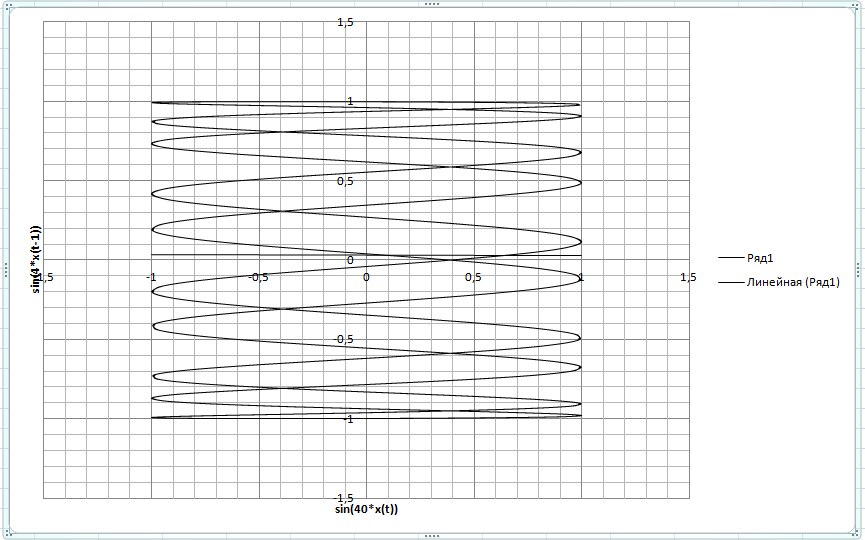
Для этого нужно создать ось аргументов, потом ось функции от аргумента и функции от предыдущего аргумента (со смещением на единицу или несколько единиц). Для увеличения рнаглядности используем функцию sin(40*x), так как в оригинальном синусе не видно этот чудесный эллипс, а он сложен почти в прямую.
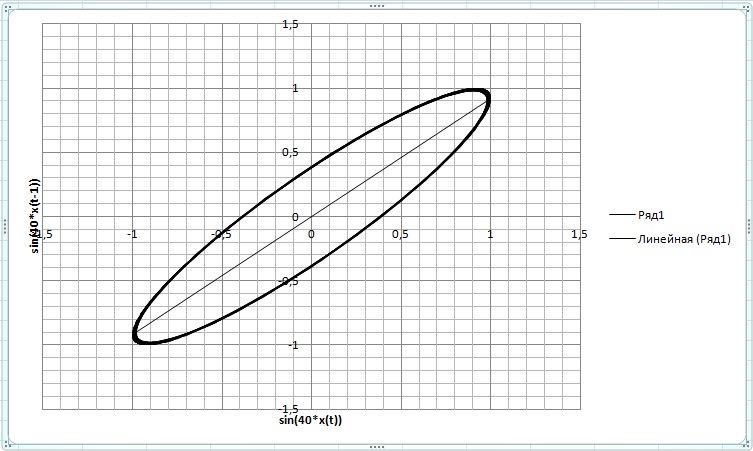
А тут мы видим красивые фигуры знакомые нам еще с университетского курса по физике, которые называются Фигуры Лиссажу ( ru.wikipedia.org/wiki/Фигуры_Лиссажу ) это портрет sin(40*x) от sin(4x) c задержкой аргумента на единицу.
Очень широко использую этот метод, для отображения наглядности «случайности процесса». Возьмем например метод линейной конгруэнтной генерации псевдослучайных чисел ( ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод ). Его портрет и обычное отображение:
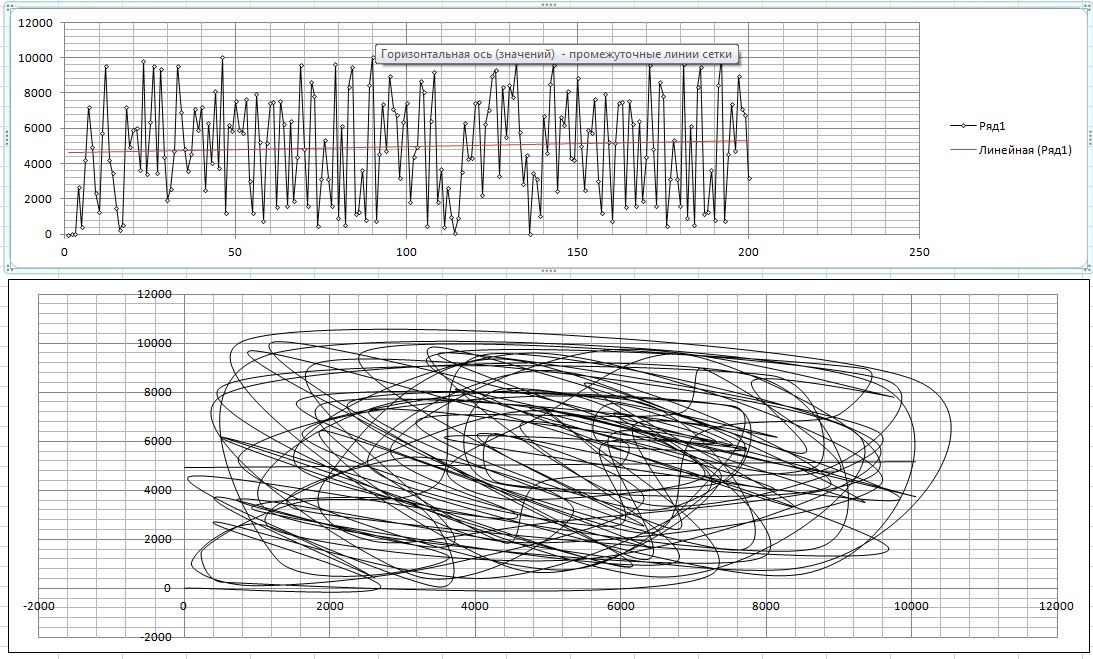
Мы видим, что похоже на клубок ниток. Таким образом — чем запутаннее(хаотичнее) клубок выглядит, тем лучше для ЛКГ.
А вот пример плохого портрета для ЛКГ, т.к. уже даже визуально наблюдаются периодичность и некоторый закон как далее:

Таким образом можно сделать вывод, что использование этого метода является наглядным способом представления изменения систем случайных чисел или же каких либо данных как в реальном времени так и с помощью заранее сгенерированных значений. Спасибо за внимание!
Автор: Kojiba