Под катом я расскажу Вам маленькую и отнюдь не шокирующую историю, большинство из вас, наверное, скажет что я надумал хоть какую-то важность этого события и что все нижеописанное является очевидным, но для меня это было маленькой победой. Если все же интересно, добро пожаловать.
Сразу хочется обговорить несколько моментов: я первокурсник, поэтому в матанализе я смысле ровном счетом ничего, ни на какое открытие не претендую и статью написал, чтобы послушать мнение местных экспертов.
Все началось с первого в моей жизни коллоквиума по дисциплине Математический анализ, одно из заданий которого содержало определение не фундаментальной последовательности по Коши. Под катом трафик.
Я, не долго думая, написал следущее:
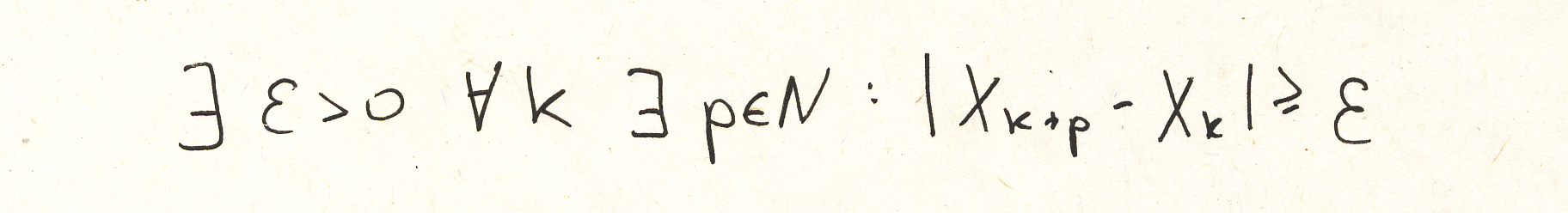
Посмотрел, прикинул и оставил. Через неделю получил свою работу с не зачтенным номером с кратким пояснением.
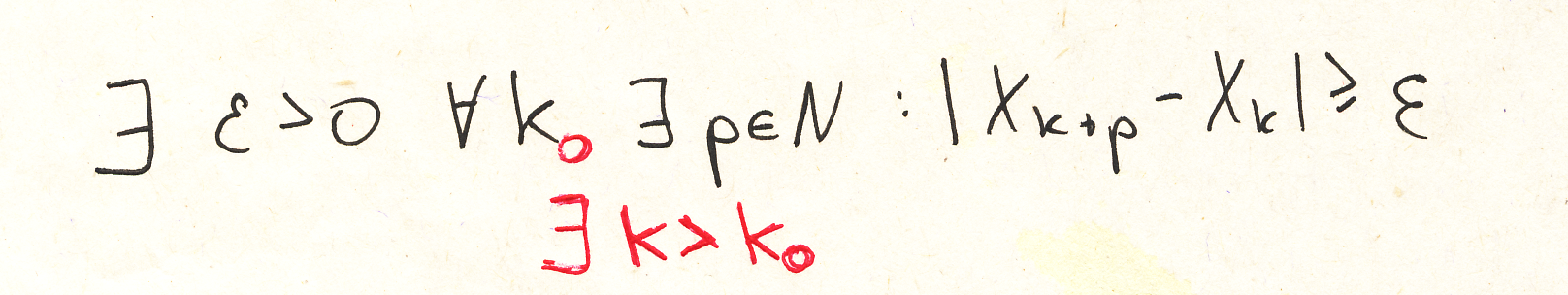
Меня это расстроило, и я решил понять, действительно ли мой вариант неправилен, решил подойти к преподавателю. После долгих дискуссий и формальных объяснений я попросил привести мне контр-пример, на что получил согласие, однако учитель обмолвился, что ему требуется время и что даже если мы не можем придумать такой пример не значит, что его нет.
Спустя пару преподаватель подозвал меня, чтобы доказать мне контр-примером то, что мое определение является лишь частным случаем. На тот момент я уже и сам склонялся к этому, однако решил выслушать. После того, как он расписал огромную и сложную последовательность, которую ваш покорный слуга, увы, забыл, он начал уже было объяснять мне и тут я понимаю, что этот пример более чем полностью удовлетворяет моему определению не фундаментальной последовательности. Уже на этом этапе моя оценка была исправлена на 5, с обмолвкой о том, что преподаватель все же убежден, что формально я не прав. Однако об оценке уже никто не думал, целую неделю я провел в размышлениях о контр-примере для моего определения.
Спустя неделю, так ни к чему и не придя, подошел я к преподавателю и рассказав о том, что я потерпел крах в поиске анти-примера, услышал, что по мнению преподавателя оба утверждения эквивалентны.
Вот доказательство, которое мы соорудили:
Доказывать будем эквивалентность утверждений фундаментальности. Возьмем отрицание от моего определения не фундаментальной последовательности.
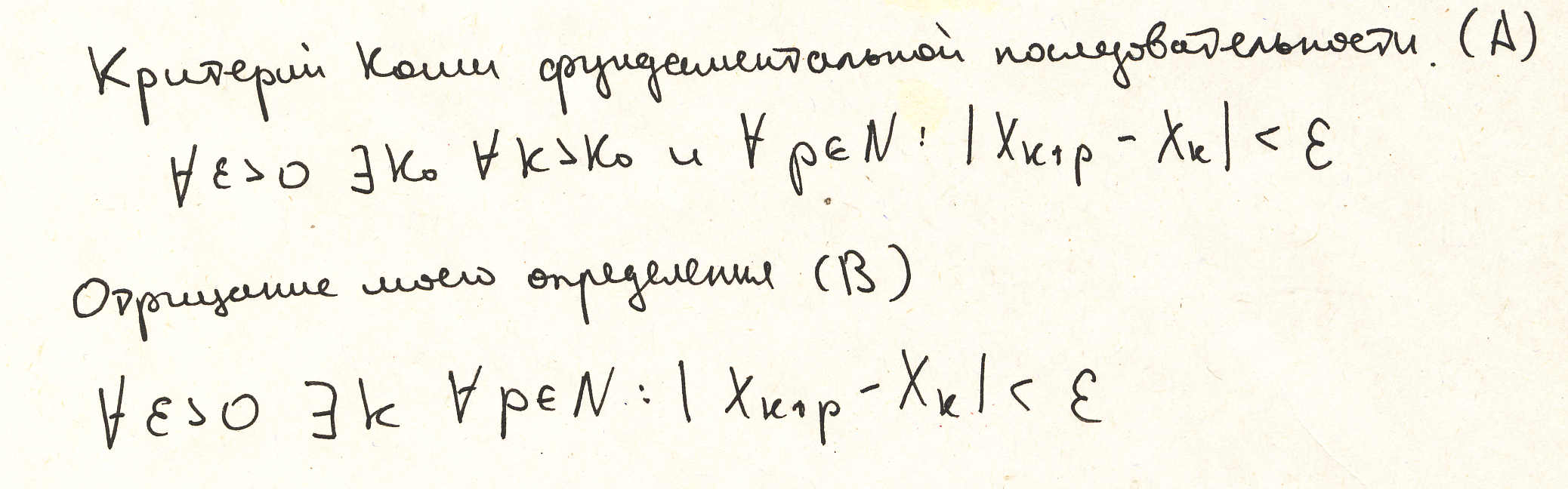
И рассмотрим два следования, чтобы доказать эквивалентность.
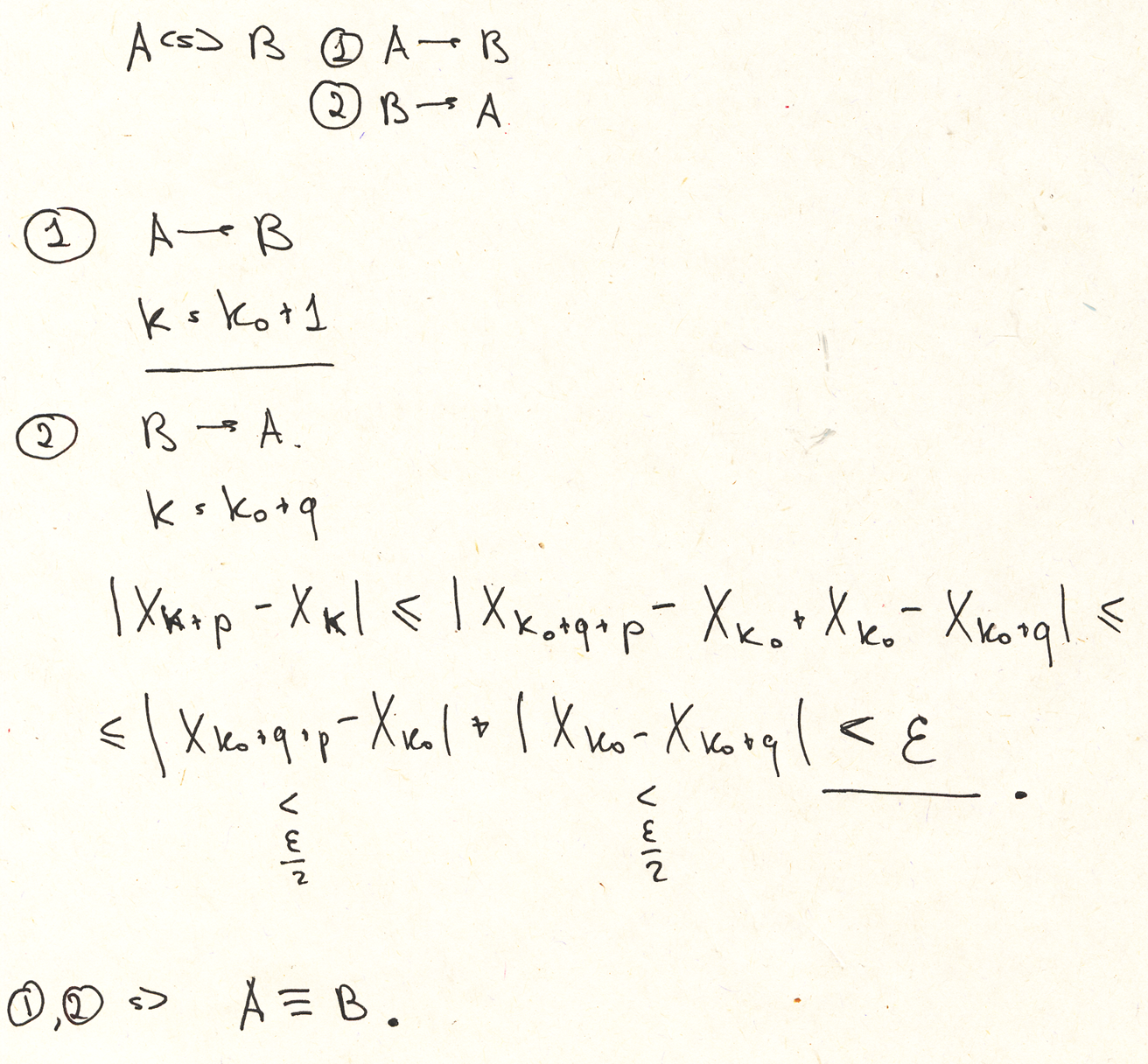
Таким образом, из определения Коши можно убрать к-нулевое, или, другими словами, не бывает таких последовательностей, которые фундаментальны / не фундаментальны до какого-то номера. Хотелось бы получить фидбек, особенно на предмет правильности доказательства.
Автор: hErrosh


