
Планировал написать про чё-нибудь эдакое мегаумное, если не про чётно-нечётную сортировку слиянием Батчера, то хотя бы про сортировку декартовым деревом. Но потом вспомнил, что грядёт череда торжеств, а значит стоит предложить что-нибудь праздничное, я бы даже сказал — легкомысленное.
Дэвид Морган-Мар

Весёлый гик из Австралии, астрофизик, математик, программист и изобретатель. Успел поработать в IBM, сейчас сотрудник Canon. Любитель комиксов, «Звёздных войн», путешествий, ненормального кодинга, миров GURPS. Автор стек-ориентированного языка программирования Chef.
На персональном сайте Дэвида Моргана-Мара есть небольшая подборка «эзотерических сортировок», о которой грех не рассказать.

Абаковая сортировка
(Abacus sort)
Предположим, нужно отсортировать набор натуральных чисел. Выложим их друг под другом в виде горизонтальных рядов из камешков в соответствующем количестве. Сдвинем по вертикали до упора.
Собственно и всё.
Если пересчитаем камешки в каждом горизонтальном ряду, то мы получим первоначальный набор чисел в упорядоченном состоянии.
Про эту сортировку я уже подробно писал, поэтому сразу переходим к следующей.
Болотно-преболотная сортировка (Bogobogosort)
Традиционно самой медленной сортировкой считается так называемая болотная сортировка.

Перемешиваем массив до тех пор, пока его элементы не упорядочатся. Временная сложность — O(n x n!).
Разумеется, любой исключительно медленный алгоритм можно сделать ещё менее продуктивным. Если в Bogosort добавить хвостовую рекурсию при проверке подмассивов на упорядоченность, то даже самое гиблое болото можно утопить в ещё более огромной трясине. Ну, а если ещё рекурсивно клонировать проверяемые подмассивы и сортировать их до тех пор пока они не совпадут с оригиналом то многого можно достигнуть и в сложности по памяти.
Основной порядок действий — такой же как и у Bogosort:
- Проверяем, отсортирован ли массив.
- Если нет, то перемешиваем его и возвращаемся в пункт 1.
А вот проверка массива на упорядоченность производится следующим образом:
- Создаётся копия массива.
- Сортируются первые n-1 элементов копии с помощью Bogobogosort.
- Проверяется, больше ли в копии n-й элемент чем первые n-1 элементов.
- Если нет, то перемешиваем копию массива и возвращаемся в пункт 2.
- Если да, то нужно ещё проверить, совпадает ли копия с оригиналом. Если совпадает, значит массив ни смотря ни на что отсортирован, если нет, то перемешиваем копию массива и идём в пункт 2.
Такое изощрённое издевательство над данными практически гарантирует что процесс будет продолжаться ну очень долго.
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Bogobogosort {
public static <T extends Comparable<T>> void sort(List<T> list) {
if (list.size() <= 1) return;
while (!isSorted(list)) Collections.shuffle(list);
}
public static <T extends Comparable<T>> boolean isSorted(List<T> list) {
List<T> copy = new ArrayList<>(list);
List<T> subList;
do {
Collections.shuffle(copy);
subList = copy.subList(0, copy.size() - 1);
sort(subList);
} while (copy.get(copy.size() - 1).compareTo(subList.get(subList.size() - 1)) < 0);
return copy.equals(list);
}
}
/* Взято отсюда: https://github.com/lucaswerkmeister/Miscellaneous/blob/master/Sorting/src/Bogobogosort.java */
Что касается сложности по времени, Дэвид считает, что где-то порядка O(n!n!). При тестировании на массиве из 7 элементов конечного результата он так и не дождался.

Сортировка «демона Максвелла» (Maxwell’s demon sort)
Метод сортировки основанный на «мысленном эксперименте» предложенном великим английским физиком XIX века Джеймсом Клерком Максвеллом. Данный способ аппаратно реализовать, опираясь на текущие достижения науки и техники, достаточно проблематично.
Ёмкость с газом разделена на две половины непроницаемой стенкой. В стенке есть отверстие, которое снабжено специальным устройством, которое назовём демоном Максвелла. Демон устроен так, что через отверстие он из левой части в правую пропускает только быстрые (горячие) молекулы газа, а из правой в левую — медленные (холодные) молекулы.
В результате функционирования данной системы якобы возникает парадокс, нарушающий Второе начало термодинамики: в сосуде исключительно за счёт внутренней энергии, без привлечения дополнительной, охлаждается левая часть и нагревается правая.
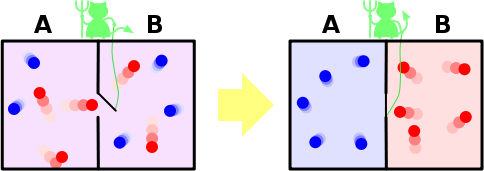
Возьмём сосуд с газом и рассмотрим все молекулы как неотсортированный набор чисел (каждое из которых — некое отображение энергии молекулы). Перегородим сосуд стенкой со встроенным в неё демоном Максвелла. Через некоторое время в правой части сосуда соберутся молекулы, чья энергия превышает некоторую заданную величину (или равна ей), а в левой части — молекулы, чья энергия меньше этой величины.
Разделим каждую половину сосуда на свои половинки с помощью стен со встроенными демонами Максвелла (для которых заданы другие пропускные значения). Таким образом мы дополнительно распределим молекулы на ещё более «горячие» и «холодные». И так мы дополнительными стенками со встроенными демонами Максвелла будем делить пространство внутри сосуда до тех пор, пока в каждой его ограниченной части не будут молекулы с одинаковой энергией. В этот момент все частицы окажутся «отсортироваными».
Сортировка Джареда Даймонда (Jared Diamond’s sort)

«Алгоритм», базирующийся на книге Джареда Даймонда (Jared Diamond) «Ружья, микробы и сталь: Судьбы человеческих цивилизаций» («Guns, Germs, and Steel: The Fates of Human Societies»).
Данное произведение, удостоенное Пулитцеровской премии, является самым значительным трудом по географической антропологии за последние полтора десятка лет. Книгу высоко оценили социологи, историки и демографы. Под впечатлением от неё был и Билл Гейтс, не последний человек разбирающийся в глобальных мировых процессах: «Впечатляет… Эта книга закладывает основы понимания истории человечества».
Ввиду обширности затрагиваемых аспектов, даже краткий пересказ изложенных в книге идей не представляется возможным в узких рамках этой небольшой статьи. Интересующиеся без труда смогут на просторах всемирной паутины найти саму книгу, а также 3-х серийный документальный фильм, снятый в 2005 году каналом National Geographic.
Теперь алгоритм.
Для каждого числа из сортируемого списка определим примитивную цивилизацию охотников-собирателей, регион их дислокации заселим дикими животными для последующего приручения и растениями для развития сельского хозяйства. Размер каждой локальной человеческой популяции, видовое разнообразие флоры и фауны — подбирать в прямой зависимости от соответствующего числа.
Позвольте развивать сельское хозяйство, промышленность, науку и культуру. То общество которое изобретёт и первым начнёт массово использовать огнестрельное оружие будет соответствовать в списке наибольшему элементу, относительно которого со временем упорядочатся все остальные.
Время выполнения зависит только от величины наибольшего числа, что позволяет формально утверждать о временной сложности O(1). На данный момент известен только один достоверный случай использования данной сортировки, затраченное время составило примерно 13000 лет. Эта величина была бы меньше, если бы наибольший элемент в массиве был бы больше.
Сортировка сбросами (Dropsort)
Проходим по массиву и удаляем (сбрасываем) из него неотсортированные элементы.

Весьма полезный, между прочим, приём со сложностью по времени O(n). Можете не благодарить.
Сортировка «Ханойская башня» (Tower of Hanoi sort)
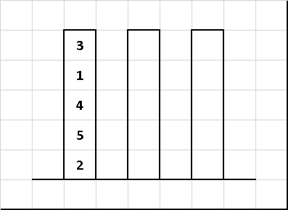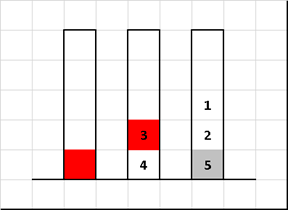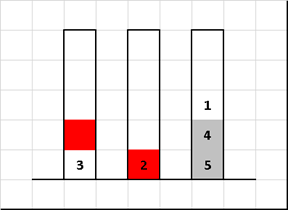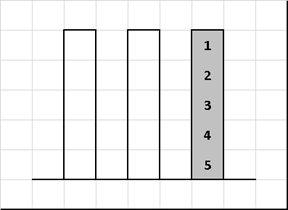
Алгоритм сортировки, основанный на знаменитой головоломке французского математика Эдуарда Люка.
Изменим только входное значение — диски на первом стержне необязательно должны быть в порядке «меньшие над большими». Остальные правила оставим как и в классике — за раз переносим только один диск, при этом нельзя «блины» большего диаметра ложить на те, у которых размеры меньше. Требуется путём переноса дисков с одних стержней на другие в итоге собрать их в упорядоченной по размеру последовательности.
Данная сортировка интересна свей необычной временной сложностью. Вырожденный случай — это… полностью упорядоченный массив. В этом случае мы имеем дело с эталонным «ханоем» для которого требуется выполнить 2n-1 перемещений. Наилучший случай по времени — реверс, в этом случае диски один за другим сразу прыгают на свои места. И вообще чем массив более близок к отсортированному состоянию, тем хуже — и наоборот!
Сортировка Разумного замысла (Intelligent Design Sort)
Поскольку для массива размером n возможно n! перестановок элементов, то вероятность того что элементы в нём будут следовать именно в том порядке в котором они следуют равна 1/n! что исчезающе мало. Абсурдно утверждать, что такое состояние массива возникло случайно.
Намного логичнее предположить, что есть некая высшая разумная сила, которая создала массив и расположила в нём элементы в определённом порядке. Нет никаких причин утверждать, что это этот порядок не оптимален. Скорее всего элементы в структуре уже выстроены именно в той последовательности, в которой необходимо, даже если это противоречит нашим призёмлённым и несовершенным представлениям об упорядоченности.
Более того — любые попытки «отсортировать» массив наверняка приведут к уменьшению изначально заложенной в него гармонии.
Автор: valemak
