Как-то мы сидели в баре с Джошем Лонгом и ещё несколькими друзьями с работы, когда он обнаружил, что я на «эй, ты!» с математикой. А он как раз недавно наткнулся на вот этот вопрос на StackOverflow и сейчас спросил меня, что это означает:

Однако, перед выяснением смысла данной китайской грамоты, думаю, стоит в принципе получить представление о том, для чего вообще это нужно. Пост в блоге Даниэля Спивака (перевод) даёт по-настоящему хорошее объяснение конечной цели алгоритма Хиндли-Милнера (в дополнение к углубленному примеру его применения):
Функционально говоря, Хиндли-Милнер (или Дамас-Милнер) — это алгоритм для вывода типов, основанный на рассмотрении того, как они используются. Он буквально формализует интуитивное знание о том, что тип может быть выведен через функционал, который он поддерживает.
Итак, мы хотим формализовать алгоритм вывода типа для любого заданного выражения. В этом посте я собираюсь остановиться на том, что означает «формализовать что-то», а затем описать «кирпичики» формализации Хиндли-Милнера. Во второй части я дам более конкретное описание этих блоков. Наконец, в третьей части я переведу вопрос со StackOverflow.
Что означает «формализовать»?
Итак, мы собираемся говорить о выражениях. Произвольных выражениях. На произвольном языке. А ещё мы хотим поговорить о выводе типов для этих выражений. И мы хотим выяснить правила, по которым мы смогли бы выводить типы. А затем мы хотим создать алгоритм, который использовал бы эти правила для вывода типов. Таким образом, нам нужен некий мета-язык. Такой, чтобы с его помощью можно было говорить о выражении на любом произвольном языке программирования. Этот мета-язык должен:
- Быть абстрактным и общим для того, чтобы позволить нам рассуждать об утверждениях вывода типа, исходя исключительно из их формы (отсюда формализация), не заботясь о содержании
- Давать точное, однозначное, но интуитивно понятное определение того, чем выражение является
- Давать это определение в терминах малого числа бесспорных примитивных понятий
- Аналогичным образом давать определение для типов, идею того, что выражение имеет тип, и идею, что мы можем вывести положение о том, что данное выражение имеет данный тип
- Поддаваться простому, краткому символическому представлению. Т.е. вместо того, чтобы говорить «выражение, сформированное путём применения первого выражения к второму выражению, имеет тип функции от строки к какому-то типу, который нам нет необходимости специализировать в данном контексте», мы можем просто сказать "
e1(e2):String→t" - Легко транслироваться во что-то, что компьютер может понять и реализовать, чтобы могли полностью автоматизировать вывод типов
Чтобы придать вышесказанному больше конкретики, давайте рассмотрим очень короткий пример формализации. Что если вместо того, чтобы формализовать язык для разговора о выводе типов выражений в произвольном языке программирования, мы захотим формализовать язык для разговора об истинности высказывания на произвольном естественном языке? Без формализации мы могли бы сказать что-то вроде:
Предположим, я знаю, что если идёт дождь, то Боб всегда берёт зонт.
И предположим, что я знаю, что сейчас идёт дождь.
Таким образом, я могу заключить, что Боб взял зонт.И любой аргумент, имеющий эту же форму, является допустимым для подобного вывода.
Исчисление высказываний формализует все эти вещи в виде правила, известного как Modus Ponens («правило вывода»):
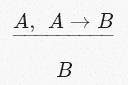
где А и В — переменные, представляющие утверждения (a.k.a. предложения или положения) в произвольном естественном языке.
А теперь давайте перечислим строительные блоки формализации Хиндли-Милнера:
Строительные блоки формализации
Нам потребуются:
- Формальный способ, чтобы говорить о выражениях. Эта формализация должна соответствовать критериям, перечисленным выше; для этой цели мы используем лямбда-исчисление. Я всё объясню буквально через минуту, но тут нет ничего сверхъестественного
- Формальный способ, чтобы говорить о типах, и формальный способ, чтобы говорить о типах и выражениях вместе. В конце-концов, цель алгоритма Хиндли-Милнера — быть способным вывести заключение вида «выражение
eимеет типt» - Формальный набор правил для получения утверждений о типе выражения через другие утверждения. Эти правила наподобие: «если я уже могу продемонстрировать, что некое выражение имеет один тип, а другое выражение — второй тип, то третье выражение будет иметь третий тип». Такой набор правил — в точности то, что вы видите в вопросе со StackOverflow. Я переведу его во всех подробностях
- Алгоритм должен разумно использовать правила вывода, чтобы из отправной точки вывести требуемое утверждение: «Интересующее меня выражение
eимеет типt». За это отвечает часть «алгоритм» в словосочетании «алгоритм Хиндли-Милнера», и в этих постах я не планирую обсуждать этот вопрос.
Чтож, поехали!
- Часть 2, в которой мы чётко определимся по пунктам 1 и 2
- Часть 3, в которой мы переведём правила вывода типов из пункта 3
Примечание переводчика: я буду очень признательна за любые замечания в личку по поводу перевода.
Автор: AveNat






