Simba: Симуляция десятков тысяч частиц в потенциале Леннарда-Джонса на чистом Python с GPU-ускорением

Добрый день, уважаемыее.

Примерно год назад я начал проект симулятора динамики частиц на Python, используя библиотеку Numba для проведения параллельных расчетов на видеокарте. Сейчас, добравшись до определенной вехи в его развитии, я решил открыть исходный код и выложить его на GitHub для всех, кому интересны подобного рода эксперименты.

Самостоятельно потыркать проект можно вот тут: https://github.com/r-aristov/simba-ps

В этой статье я кратко опишу суть проекта, пройдусь по прилагающимся к нему примерам и расскажу почему вообще начал работу над ним.

Да кто такие эти ваши Леннард и Джонс?

На самом деле, это не два разных человека, а один - Сэр Джон Леннард-Джонс, который сотню лет назад придумал относительно простую физическую модель взаимодействия точечных частиц. Физически она задает потенциальную энергию взаимодействия пары частиц в зависимости от расстояния между их центрами.

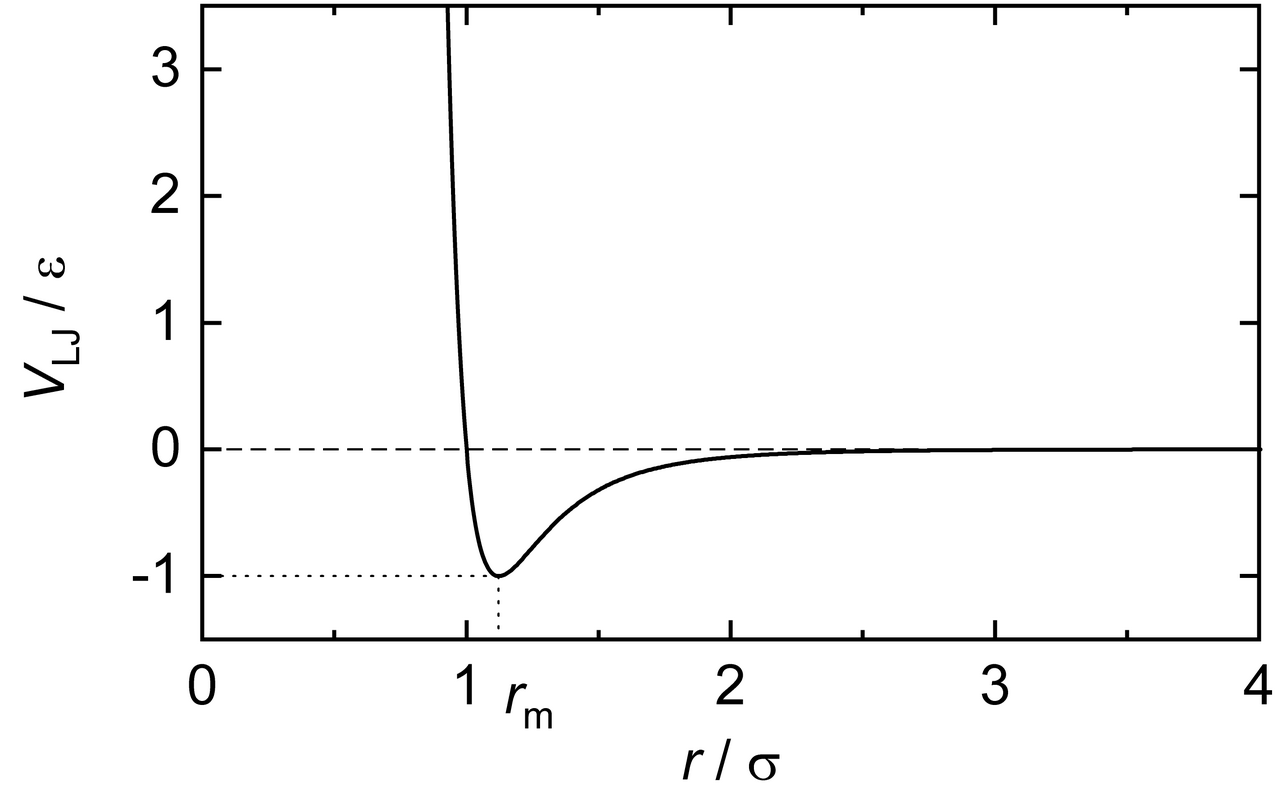
Как таковых радиусов у частиц нет, они представлены не шариками в пространстве, а именно точками, у которых есть координаты и скорость. Вместо этого сам потенциал имеет два параметра - глубину потенциальной ямы, задающую минимальную энергию, которой могут обладать взаимодействующие частицы, и расстояние , на котором должны находиться частицы, чтобы этой минимальной энергией обладать.

В нуле потенциал улетает в бесконечность, не позволяя частицам пролетать друг через друга, по крайней мере, так это выглядит в идеальном мире теоретических расчетов. В численной симуляции, разумеется, все зависит от реализации - эта бесконечность в точке 0.0 порождает всякие забавные ситуации, в которых быстрые частицы влетают друг в друга с такой энергией, что начинают туннелировать прямо сквозь соседей, причем это сопровождается бесконтрольным ростом их и так немалой кинетики, из-за чего симуляция "взрывается".

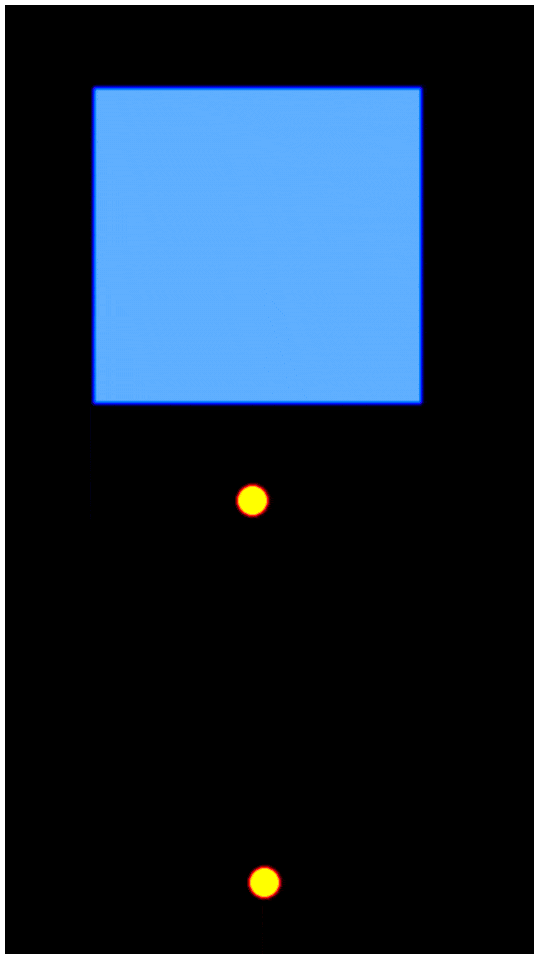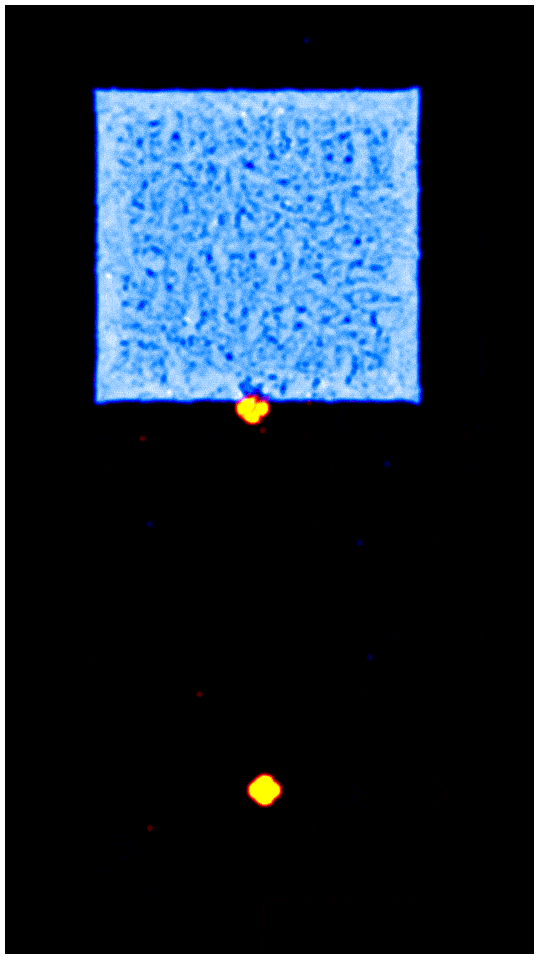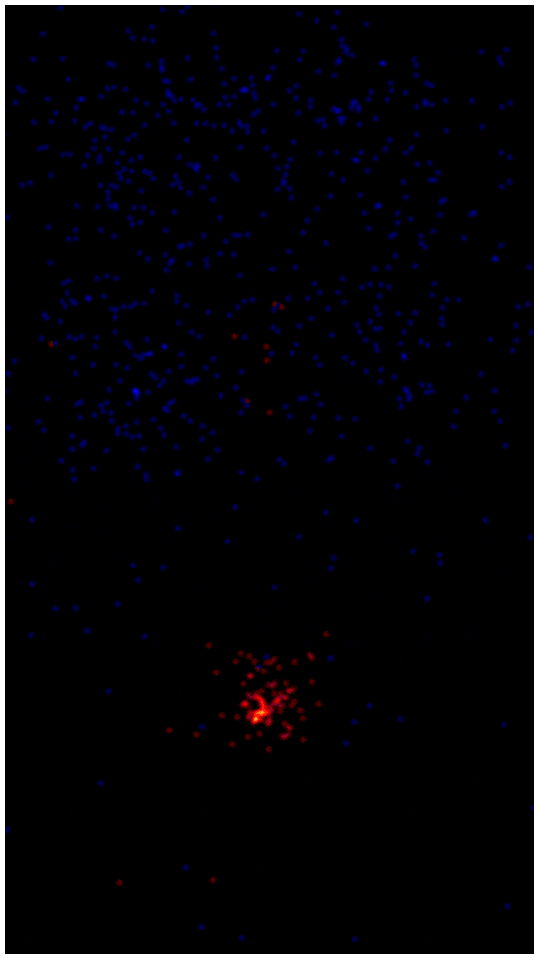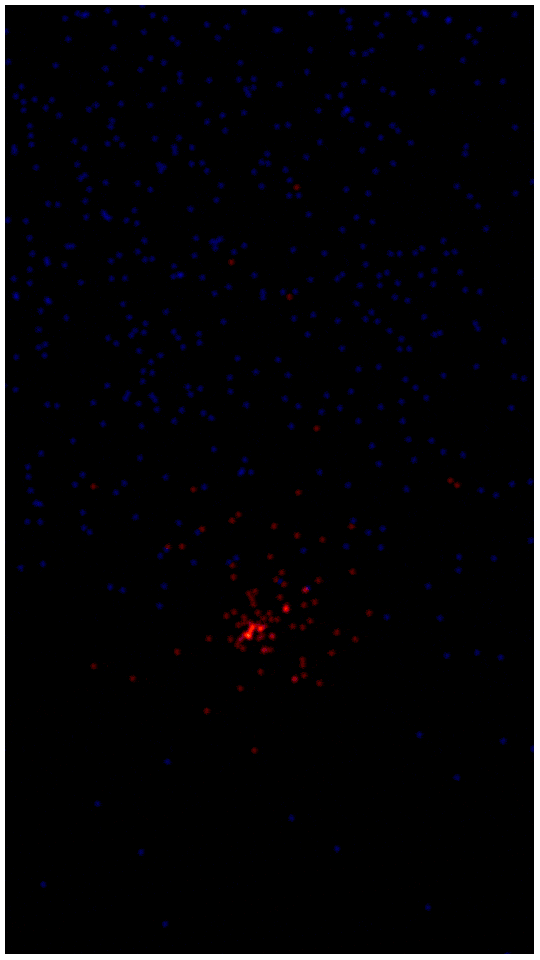
Впрочем, об этих особенностях я подробнее расскажу в следующих статьях. По форме этого потенциала можно заметить, что он обеспечивает не только отталкивание чересчур сблизившихся частиц, но и притяжения на малых расстояниях - это именно то, что отличает его от простой реализации отталкивающихся "бильярдных шариков" - благодаря притяжению частицы не просто разлетаются в стороны, а формируют макро-структуры, которые можно заметить на гифке из заголовка. Кстати, в readme репозитория есть эта и другие гифки в куда более приятном глазу качестве.

А что он может?

Именно за счет этого двойного действия (притяжения на одних расстояниях и отталкивания на других) одна эта простая формула порождает удивительное множество эффектов, которые могут быть промоделированы относительно простым кодом. Все, что нужно - это продифференцировать ее по переменной , чтобы получить величину силы, действующей на частицу (ведь как мы помним - сила - это минус производная от потенциала!), написать сносный численный интегратор, что-нибудь сделать с квадратичным ростом количества взаимодействий, чтобы видеокарта не расплавилась от натуги, и как следует это все распараллелить для вычисления на GPU. И чтобы вам не пришлось этим заниматься, я это сделал за вас в своем симуляторе Simba (что означает Simulation with Numba).

Это - первая обзорная статья, поэтому тут я не буду вдаваться в глубокие подробности реализации. Если заинтересует - распишу все это в последующих материалах. Скажу только, что я реализовал интегрирование Вереле [Verelet], а также для эксперимента - Рунге-Кутту и некий интегратор Йошиды, но последние два не вошли в релиз, так как показали себя хуже стандартного Вереле. Чтобы распараллелить вычисления и избежать квадратичного роста вычислительной сложности я использую то, что в зарубежных материалах называется hash-grid. Я предпочитаю называть это "enforcing locality" - информация о частицах сохраняется в 2д карте в соответствии с их позициями, этим мы как бы принуждаем взаимодействия к локальности, каждая частица при расчете сил смотрит только на небольшую область вокруг себя и берет информацию об окружении из этой 2д карты. А так как видеокарты позволяют проводить расчеты в тысячи потоков, каждая частица, по сути, обсчитывается независимо от других.

Итак, что же можно моделировать при помощи потенциала Леннарда-Джонса и Симбы в частности?

Виртуальная химия

Ну, например, можно вместо одного типа частиц сделать четыре, и для каждой возможной пары взаимодействующих типов частиц задать свои значения глубины потенциальной ямы и оптимального расстояния. Это приведет к тому, что частички будут взаимодействовать друг с другом по-разному, формируя молекулы. Вот, например, симуляция экзотермической реакции, в которой изначально есть два типа молекул - красно-синие и зелено-желтые. И те и те состоят из 5 частиц, одной синей в окружении четырех красных и одной желтой в окружении четырех зеленых. Это достаточно стабильная конфигурация, а красные с зелеными не особо взаимодействуют, поэтому эти молекулы просто легонько отталкиваются друг от друга, оставаясь целыми. Но связь желтой частицы с синей на несколько порядков более энергетически-выгодная, чем все остальные! Поэтому достаточно лишь легкого толчка, чтобы началась самоподдерживающаяся экзотермическая реакция. В видео в качестве такого толчка выступает несколько свободных желтых частичек, одну из которых я пинаю в сторону красно-синей молекулы. Не будучи окруженной экранирующими ее зелеными частицами, она стремиться провалиться в глубочайший потенциальный колодец синей частицы, разрывая красно-синюю молекулу на части.

Кстати, если фраза "в реакции выделяется энергия" вам всегда казалась туманной, то вот - это именно так и происходит. Стремясь занять более энергетически выгодное положение, частицы разрывают стабильные молекулы и их осколки с огромной скоростью летят во все стороны, разбивая все новые молекулы и открывая высокоактивные желтые и синие частички для новых реакций.

А если эту смесь потом охладить, они начинают слипаться в длинные полимерные цепочки.

Это, наверное, наиболее интересное видео из категории "виртуальная химия", остальные помещу под спойлер.

Леннард-Джонсовский самогон

Перейдем из микромира в макромир. Всё той же формулой описываются и газы, и жидкости и твердые тела. Разница только в том, какова глубина потенциальной ямы и какова энергия частиц - хватает ли ее только на колебания около оптимального положения, или частицы могут вылететь за пределы этих связей. А это значит, что "леннард-джонзиум" (так иногда зовут это виртуальное "вещество") можно кипятить и замораживать, и он будет менять свое состояние в соответствии с самой настоящей фазовой диаграммой. Но не будем его кипятить просто так, лучше будем перегонять в виртуальном перегонном кубе!

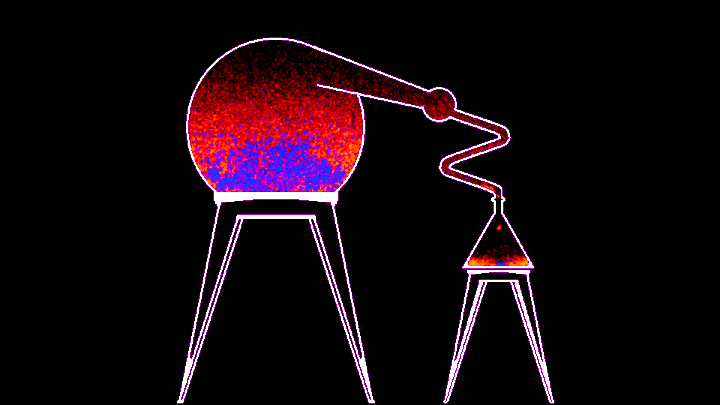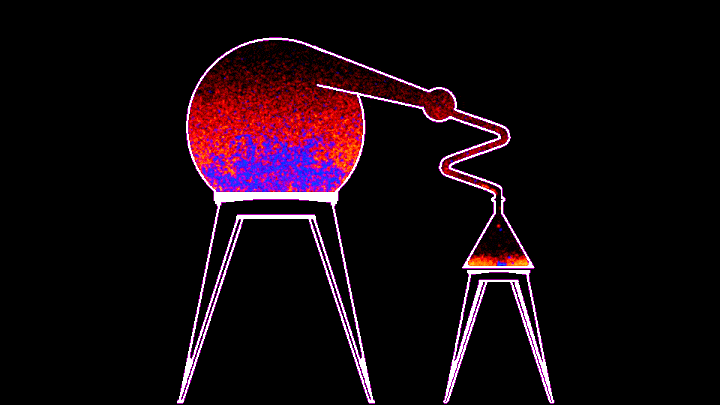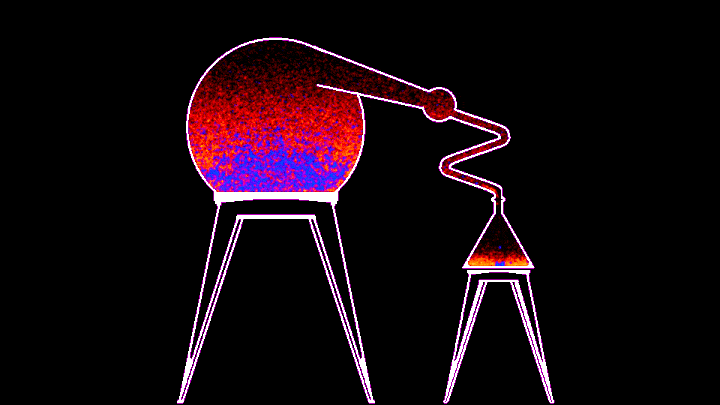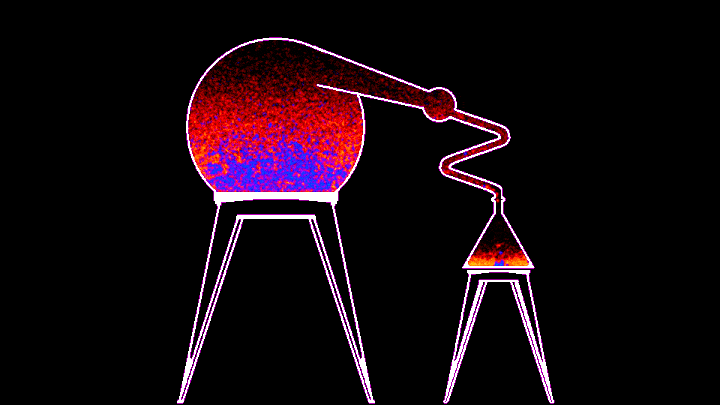
Процесс, к сожалению, не очень быстрый - гифка ускорена в 10 раз, но из этого, на мой взгляд, могла бы получиться неплохая механика для игры про алхимию. В примере, который идет вместе с симулятором, можно менять температуру нагревателя из командной строки, а в самом коде можно поменять энергию связи красного и синего веществ (то бишь глубину потенциальной ямы). По дефолту у синего вещества она в 14 раз больше, значит его частицам надо в 14 раз больше энергии, чтобы вылететь за пределы потенциальной ямы, поэтому первым испаряется красное. В змеевике расположен виртуальный термостат, охлаждающий пролетающее через него вещество, из-за чего оно конденсируется и капает в колбу.

Правда, в этом видео еще прошлый вариант установки, чуть менее эстетичный, поэтому к релизу я ее перерисовал.

Кстати, самое время сказать о том, как происходит конфигурация симулятора. На вход идет буквально картинка из пеинта - в самом начале разработки я решил, что так мне будет проще всего - не надо городить какой-то особый редактор, просто рисуешь в пеинте картинку, а в коде буквально парой строк задаешь соответствие цвета из картинки параметрам частиц. Белый цвет воспринимается как пустое пространство, любой другой можно использовать в соответствии со своими замыслами. Симуляция столкновения, как в заголовке, например, требует входной картинки (или можно, при желании, разместить частицы кодом) и строк 10 кода, половина из которых - это настройка камеры и рендера. Для симуляции дистилляции нужно все то же самое, плюс еще пара строк, задающих работу термостатов.

Детерминистический хаос

Одна из моих любимейших тем в исследованиях. Хаотические и детерминистические системы, в которых можно воочию увидеть, как может процесс быть одновременно детерминистическим, непредсказуемым на практике и меняющими траекторию в своем фазовом пространстве при микроскопических, едва заметных изменениях.

Симба - детерминистический симулятор. Ну, то есть, это можно включить параметром deterministc=True. А это значит, что можно прогнать симуляцию, потом присвоить, скажем, цвета частичкам в соответствии с их финальным положением, а после запустить симуляцию заново и смотреть, как из хаоса рождается картинка.

Это, кстати, работает как неэффективная, но прикольная криптография. В том смысле, что эта система невероятно чувствительна к начальным параметрам - достаточно поменять буквально любой параметр любой из частиц (позицию, скорость) даже на одну десятимиллиардную, и картинка уже не сложится. Тут в качестве зашифрованного сообщения выступает информация о том, какие цвета какой частичке были присвоены, а в качестве ключа - любой набор любых параметров начального состояния. Более подробно весь процесс показан в видео под спойлером. И там же еще пара видео на этом же эффекте, которые я отрендерил, работая над детерминизмом Симбы.

Кстати, это оказалось не такой уж тривиальной задачей - это в школьной арифметике от перемены мест слагаемых сумма не меняется, а в суровой взрослой жизни операция сложения чисел с плавающей запятой неассоциативна из-за конечной точности представления. А это значит, что если мы будем, скажем, общую силу, действующую на частицу, считать параллельно и просто прибавлять ее компоненты к какому-то аккумулятору, результаты будут отличаться от запуска к запуску - видюха-то считает вразнобой, порядок каждый раз разный. Но этот эффект можно победить. В целом, даже без какого-либо ощутимого оверхеда, но я все равно сделал детерминизм отключаемым, на всякий случай.

Чтобы не захламлять статью, не буду сюда перекладывать гифки из ридми на гитхабе, тем более, что они весьма тяжелые - алгоритмы сжатия с большим трудом прожёвывают такие картинки из-за огромной энтропии теплового движения частиц. Там есть еще несколько примеров, чуть более простых, чем перечисленные тут - столкновение, которое я вынес в заголовок поста, оно же, но с другой визуализацией, без сглаживания, зато с цветом частиц, соответствующим величине их вектора скорости, разноцветные частички в ячейках, отличающиеся температурой...

Еще Симба вполне тянет несколько десятков тысяч частиц в реалтайме, так что можно его использовать как часть игрового движка. У меня на ютуб канале есть пара видео с реалтаймовыми экспериментами. В релиз такие примеры вкладывать уже не стал, но запустить симулятор в таком режиме - задача тривиальная, любой знакомый с PyGame или с разработкой оконных приложений, справится с этим без труда.

Осталось ответить на главный вопрос.

Зачем все это?

Ну, во-первых - это прикольно. Меня завораживает сама идея того, что из одного простого уравнения (из двух, если считать закон Ньютона) может вырасти система, обладающая таким широким спектром разнообразных свойств - тут тебе и жидкости, и газы, и дистилляция, и воронки, и детерминистический хаос. У меня даже получилось из этого джонзиума буквально выплавить струну - вот прямо "залить" его в форму и охладить, чтоб частички заняли оптимальное положение - и она звучала! Хреново звучала, постоянно рвалась, но все-таки.

Я давным-давно хотел этим заняться, и вот год назад решил, что no time like the present, и что откладывать так можно вечно, и если я этим не займусь, то так и не увижу то, что хотел увидеть реализованным. Ну, а выложил код я чтобы те, кому это так же интересно, могли сразу поэкспериментировать. Как говорится, я потратил год на этот код, чтобы вам не пришлось.

Во-вторых, мне вот всегда было интересно - а паровую машину так можно сделать?

Оказалось - можно.

Здесь Симба отвечает за частицы и поршни, а физику маховика и кривошипно-шатунного механизма я прикрутил сверху, в питоне, но это не единственный вариант)

Я не стал пихать этот код в релиз, потому что, честно говоря, его надо бы еще тестить и оптимизировать, а у меня сейчас другие дела, но я-таки реализовал физику твердых частиц прямо внутри симулятора. А это значит, что эту паровую машину можно построить из частичек прямо целиком. А еще всякие ракеты с разными формами сопел, пробки, вылетающие под давлением из бутылок и тому подобное. Под спойлером видео с примерами таких экспериментов.

Ну и наконец, главная причина, которую я приберег напоследок. На самом деле, я уже давно занимаюсь машинным обучением, и больше чем детерминистический хаос люблю только нейронные сети (которые, кстати, будучи нелинейными системами, тоже демонстрируют такое же поведение). Мне всегда было интересно, какие знания и как можно дистиллировать в коэффициенты современных сеток. Получится ли обучить ее динамике частиц? А как будет выглядеть выход за установленные пределы по энергии - обычная симуляция просто взрывается, а как себя поведет сеть? А можно ли "на дурачка" промоделить жидкости на уровне частиц, а в сетку дистиллировать знания об их усредненном поведении, чтобы она сама вывела внутри себя аналог уравнений CFD (computational fluid dynamics, уравнений динамики жидкостей), и потом использовать для симуляции уже ее, не симулируя сотню тысяч частиц? Так как симулятор реализован на чистом Питоне, он элементарно стыкуется хоть с PyTorch, хоть с Tensorflow, и позволяет построить быстрый и эффективный пайплайн для обучения.

Не так давно я добрался до значимой вехи в этом проекте и-таки обучил сетку считать физику частичек вместо Симбы.

После этого я и стал готовить опенсорсный релиз симулятора. Сейчас релиз готов, а это значит, что я возвращаюсь к своим исследованиям и с радостью буду делиться с вами дальнейшими результатами.

На этом у меня все, подписывайтесь на мой телеграмм-канал, где я делюсь рабочими моментами исследований и просто заинтересовавшими меня вещами, а также на мой ютуб-канал, куда я выкладываю свои визуализации экспериментов. Хорошего вам дня!