Сегодня я расскажу о процессе, который я придумал для преобразования SVG-контура в векторный рисунок верёвки.
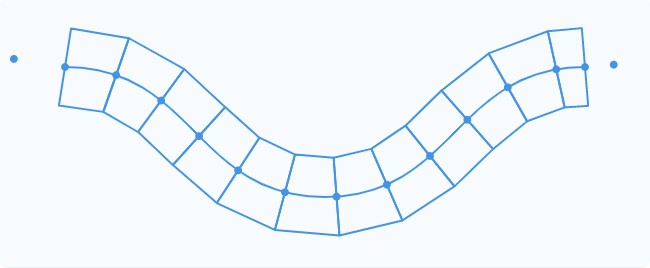
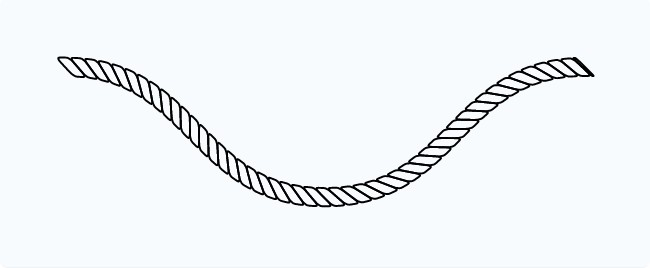
Вы узнаете, как превратить показанный слева контур в верёвку справа:

Эта задача возникла в проекте, над которым работали мои коллеги, и она привлекла моё внимание. Я думал о ней и начинал экспериментировать, как только появлялось свободное время. Это было очень увлекательно, поэтому я захотел поделиться с вами процессом решения.
Стоит учесть, что это не туториал по кодингу, а подробный обзор каждого из этапов. Но не беспокойтесь, код полностью доступен.
Если вам не терпится, то можете сразу перейти к интерактивному демо в оригинале статьи или изучить код на CodePen. Но сначала я рекомендую вам прочитать всю статью.
Замысел
Взглянув на это фото верёвки, вы заметите, что она состоит из множества переплетённых друг с другом прядей. Визуально они делят верёвку на сегменты. 2D-проекция каждого сегмента напоминает изогнутый многоугольник.
Наша задача будет заключаться в создании этих многоугольников при помощи JavaScript.
Мы начнём с генерации простых прямоугольных многоугольников. Затем мы изменим их так, чтобы сделать похожими на настоящие сегменты верёвки.

Как подходить к решению подобных задач
Мне кажется, это одна из тех задач, которые может решить и нарисовать на бумаге ребёнок. Но в то же время сложно разбить её на части и превратить в код.
Я замечал, что многие джуниор-разработчики испытывают трудности с похожими задачами. Обычно они сразу же приступают к кодингу, а затем запутываются в своём коде и заходят в тупик. Именно поэтому так важно сначала решить задачу. (Я до смерти утомил своих джунов, над которыми менторствовал, повторяя, что программирование — это решение задач, а код — лишь инструмент для решения этих задач.)
Я мыслю визуальными образами. Рисование на бумаге упрощает для меня решение любой задачи. Рекомендую вам тоже это попробовать. Держите рядом с компьютером ручку и бумагу, и пользуйтесь ими, прежде чем начнёте писать код.
Порисовав разные верёвки, я довольствовался картинкой, которую вы видите в нижнем правом углу левой страницы:
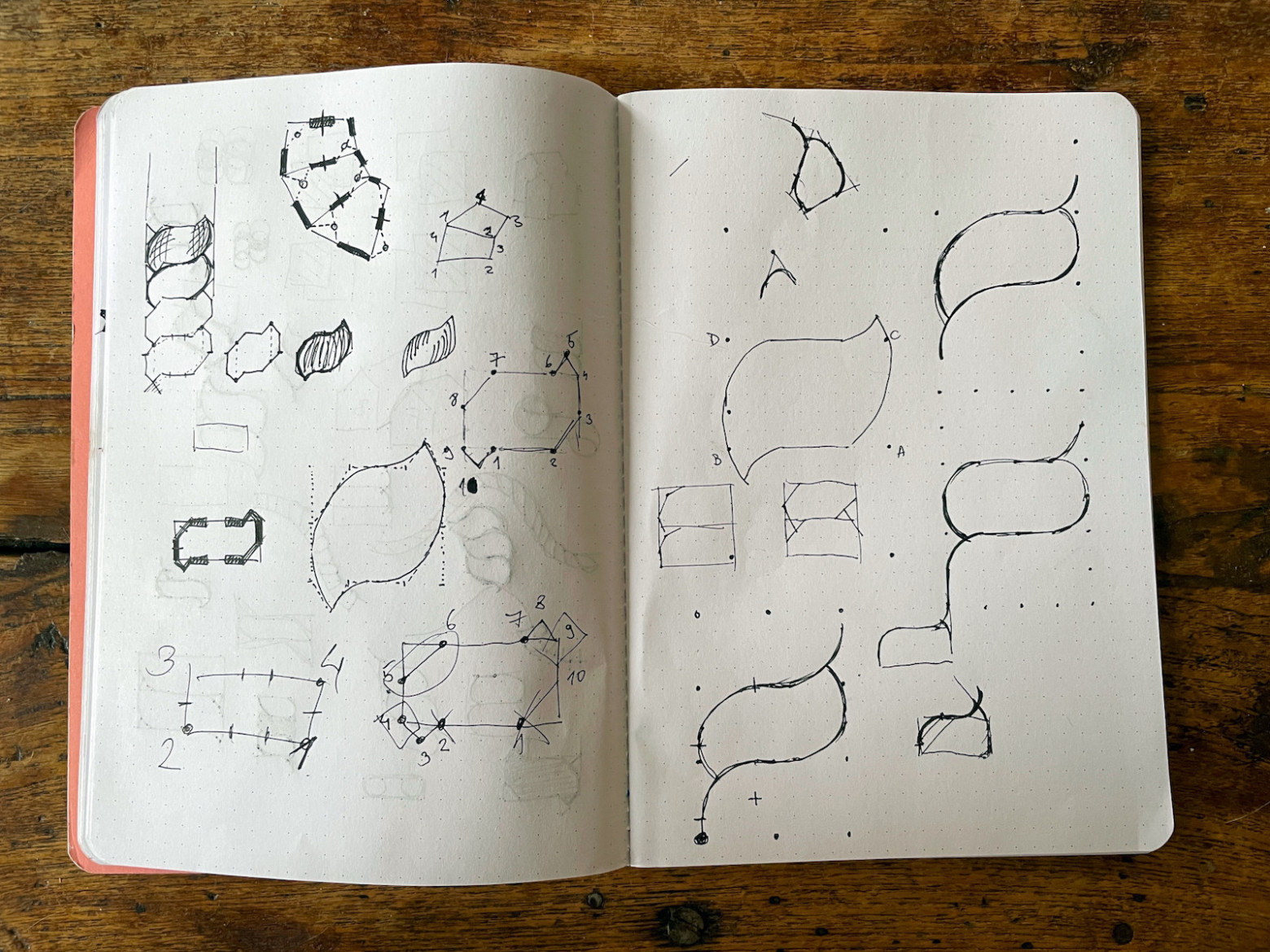
Она неидеальна, но проста и её легко превратить в код. Именно поэтому я выбрал её в качестве опорной точки, и только после этого начал кодить.
Процесс
Начинаем с SVG-контура

Наша задача — создать программу, превращающую любой SVG-контур в верёвку. Программа должна будет поддерживать сегменты из прямых отрезков (полилиний) и кривые Безье.
Давайте начнём с простого искривлённого контура, показанного выше.
<path
d="M 50 150
C 150 150, 150 50, 250 50
C 350 50, 350 150, 450 150"
/>Разбиваем контур на равные части

Если мы разделим контур на части, то сможем использовать каждую часть для одного сегмента верёвки. Чтобы разбить контур, нам нужно пройти по нему и вычислить точку через каждые n пикселей.
Для этого нам нужно как-то получить общую длину контура, чтобы мы знали, когда прекращать итерации, а также для того, чтобы функция добралась до точки в нужной длине.
К счастью, браузеры нативно предоставляют нужные нам методы:
-
getTotalLength возвращает длину контура.
-
getPointAtLength возвращает точку на заданном расстоянии по контуру.
Удобно здесь то, что нам не нужно рендерить контур на странице. Оба методы работают с контуром, находящимся только в памяти.
Ниже представлена функция, которую я использовал для вычисления этих точек:
function getPathPoints(d, step = 10) {
const path = document.createElementNS("http://www.w3.org/2000/svg", "path");
path.setAttribute("d", d);
const length = path.getTotalLength();
const count = length / step;
const points = [];
for (let i = 0; i < count + 1; i++) {
const n = i * step;
points.push(path.getPointAtLength(n));
}
return points;
}Наверно, вы заметили две дополнительные точки недалеко от концов контура. Они не включены в показанный выше фрагмент кода. Пока не обращайте на них внимания, мы используем их позже.
Примечание о рендеринге на стороне сервера.
Эти методы не работают на стороне сервера. Однако я проверил несколько серверных языков и почти во всех них есть разновидности этих двух методов. Для NodeJS, вероятно, можно использовать библиотеку svg-path-properties.
Добавляем толщины
Разбив контур, нужно придать каждому сегменту толщину. Мы сделаем это, отрисовав через каждую точку линию нормали.
В нашем случае нормали не должны быть математически точными, достаточно аппроксимации. Есть простой способ аппроксимации нормали к кривой, для него нужны три последовательные точки.

На рисунке выше показана нормаль, проведённая через точку P. Она задаётся биссектрисой угла α между точками Pp, P и Pn. Точки Pp и Pn являются вспомогательными. В качестве вспомогательных мы будем использовать предыдущие и последующие точки.
Если вы подумали, что именно для этого я добавил на предыдущем этапе две дополнительные точки, то вы правы! Они добавлены для того, чтобы у первой и последней точки тоже были соседи с обеих сторон.
К счастью, у меня уже был код, потому что я решал такую же задачу в своём проекте Vertigo.

Объединяем нормали в сегменты
Об этом этапе сказать особо нечего. Нам просто нужно соединить пары соседних нормалей, что даст нам блочные сегменты. Давайте попробуем скруглить их углы, чтобы сделать их интереснее.
Скругление углов сегментов
Для скругления сегментов мы используем методику Чайкина, то есть алгоритм рекурсивного разделения для генерации кривых. Алгоритм берёт каждый отрезок многоугольника и находит на обеих его сторонах две точки на указанном расстоянии (обычно лучше всего подходит 0,25 от длины). Затем он заменяет исходную точку двумя новыми. Далее мы рекурсивно повторяем весь процесс, пока не будем довольны результатом.
Звучит сложнее, чем есть на самом деле. Думаю, пример ниже поможет вам разобраться. (В оригинале статьи пример интерактивен.)
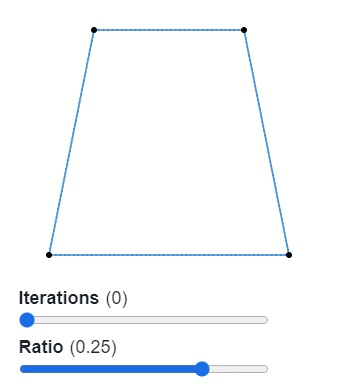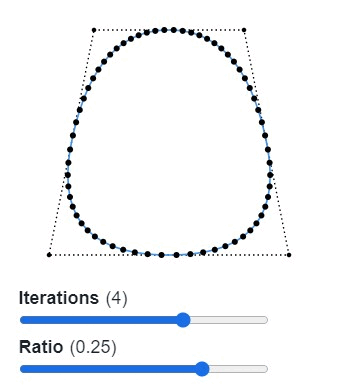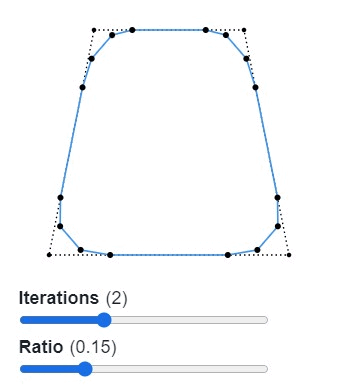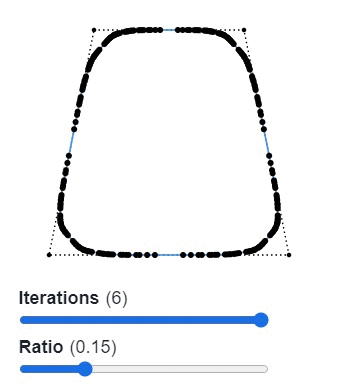
Этот способ скругления возвращает не кривые Безье, а полилинию. Во многих случаях это хорошо, поскольку геометрические операции проще выполнять с полилиниями, чем с кривыми Безье. Всё равно при достаточном количестве итераций человеческий глаз не увидит разницы.
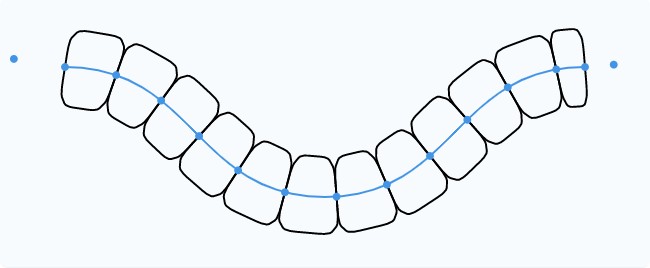
Изгибаем сегменты
Реальная верёвка создаётся скручиванием множества нитей. Для имитации скручивания нам нужно изогнуть сегменты. Мы легко можем это сделать, повернув биссектрису на фиксированный угол.
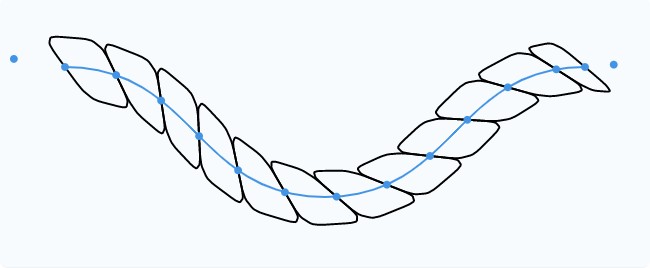
Закончим на этом?
Если удалить вспомогательные элементы и сделать весь объект тоньше, то он начинает напоминать верёвку. Если вам этого достаточно, то можете на этом остановиться.
Но если взглянуть на фото верёвки в начале статьи, то мы увидим, что наши полигоны не полностью передают её форму. Они почти равномерные, а на фото сегменты накладываются друг на друга и идут один под другим.
Так что давайте продолжим и попытаемся сделать наши сегменты более похожими на сегменты реальной верёвки.
Улучшаем сегменты
Нужно вернуться к наброску в блокноте, который я показывал в начале статьи. Мы временно уберём изгиб сегментов, чтобы нам было проще разбираться.
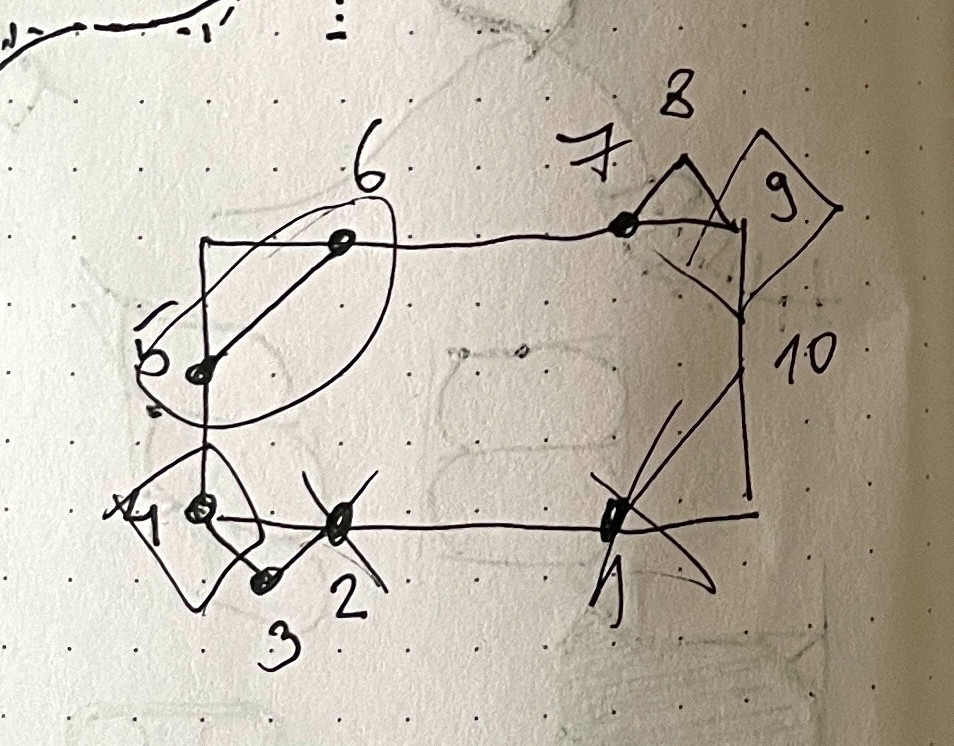
Нужно отрезать два угла сегмента и добавить два конца, обозначенные на эскизе как точки 3 и 8.
После реализации этого плана сегменты кажутся слишком блочными и математическими. (К сожалению, я не сохранил код, так что не могу показать пример этого.) Однако я знал, что двигаюсь в нужном направлении. Затем я начал подстраивать изображение, перемещая точки. Результат показан на изображении ниже; думаю, теперь сегменты выглядят намного естественнее и округлее.
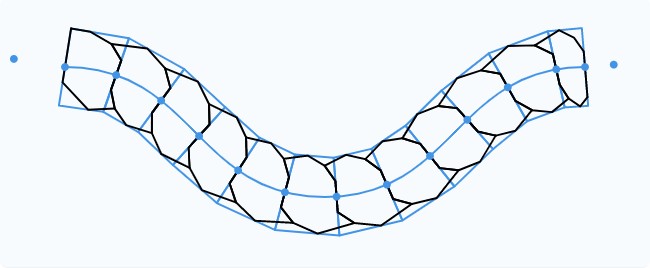
Прежде чем двигаться дальше, обратим внимание, что первый и последний сегмент немного отличаются, поскольку не зажаты между двумя другими сегментами. Именно поэтому в коде они обрабатываются не как все остальные сегменты.
Снова скругляем сегменты
Если мы применим алгоритм Чайкина к новым сегментам как к замкнутой полилинии, то получим следующее:
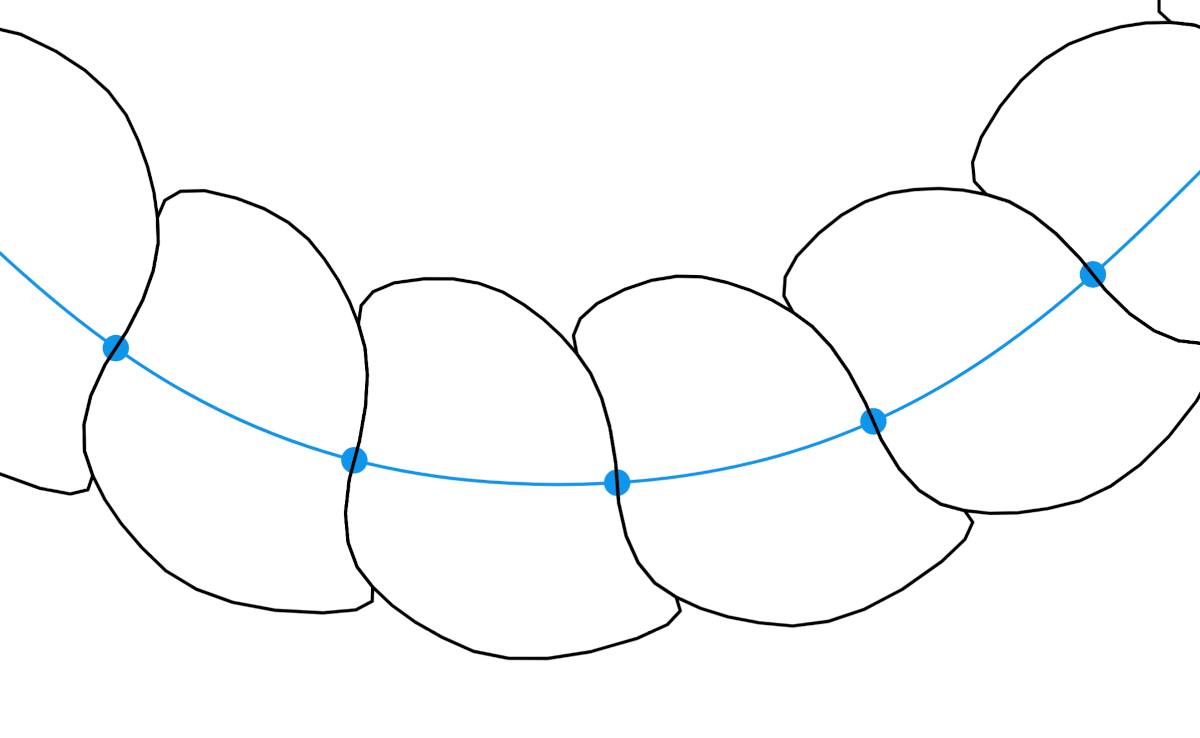
Всё красиво и скруглено, но выглядит странно, мы отдаляемся от иллюзии скрученности. Было бы лучше, если бы мы сохранили два острых угла.
Чтобы сохранить углы, мы разделим отрезок сегмента на два отреза, а затем применим алгоритм скругления по отдельности к каждому из них. Это создаст более правдоподобную иллюзию того, что нити идут одна за другую.
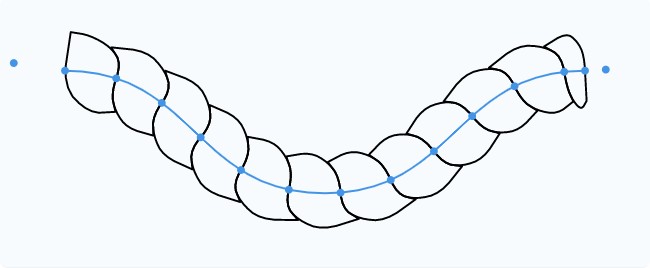
Устраняем зазоры (необязательно)
Возникает небольшая проблема, заметная после этапа скругления. Появляются мелкие зазоры, потому что в процессе обработки удаляются точки.
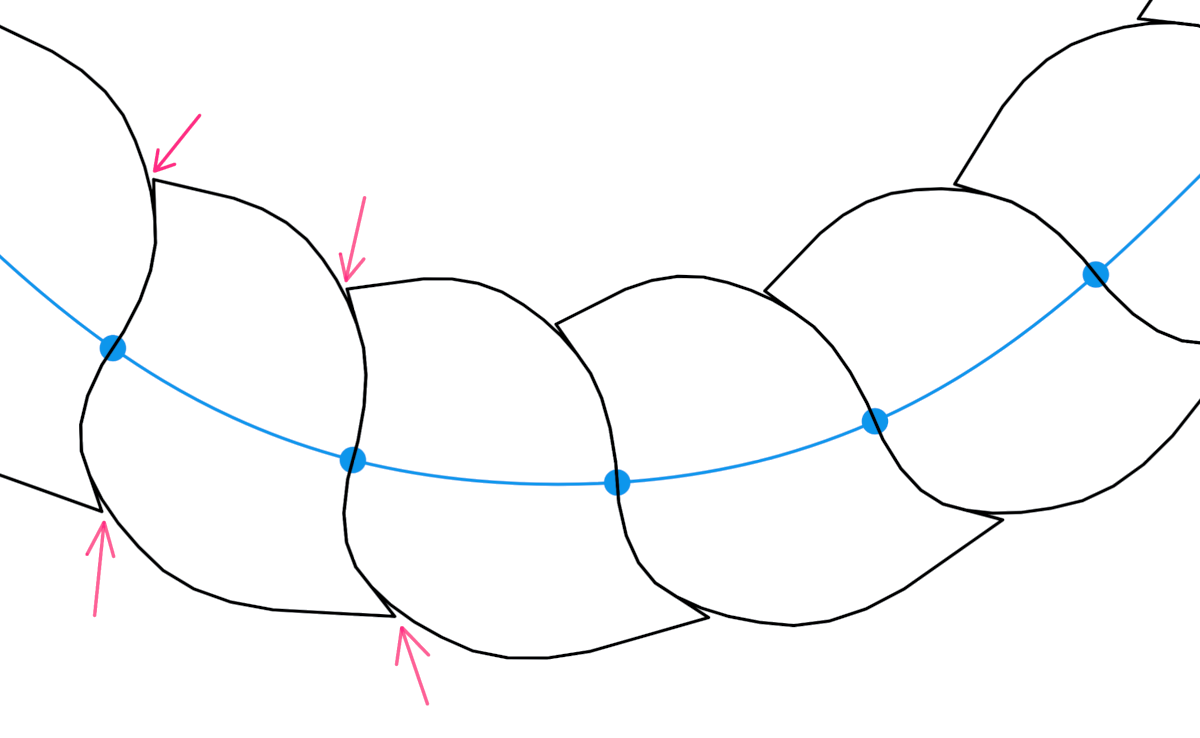
Мне они не мешают, потому что заметны только при очень тонких контурах. Толстые контуры всё красиво прикрывают.
Я устранил эти зазоры, но только ради решения интересной задачи. Есть хитрая методика спасения точки от удаления при использовании алгоритма Чайкина — утроение этой точки. Таким образом мы создаём две грани нулевой ширины. Не важно, сколько раз мы будем выполнять рекурсивное разделение, любая доля от нуля всё равно будет равна нулю.
Однако у этого трюка есть и недостаток. При каждой итерации он будет дублировать все три точки. Поэтому если вы воспользуетесь этой методикой исправления, то вам может потребоваться подчистить дублированные точки.
Как я уже говорил, меня зазоры не волнуют, поэтому на последующих этапах я отключил это исправление.
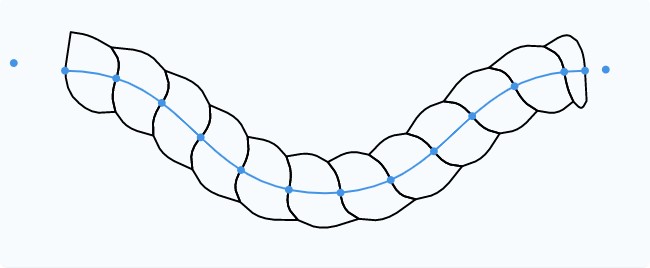
Снова изгибаем сегменты
Давайте снова изогнём всю верёвку. Как и раньше, просто повернём биссектрису на фиксированный угол.

Добавляем цвет
Удалим вспомогательные элементы и добавим цвет. Надо сказать, выглядит уже как настоящая верёвка! Но мы ещё не закончили.

Анимируем
Можно даже анимировать верёвку. Анимация может быть полезной для графиков. Но, честно говоря, мне хотелось просто поразвлечься.
Не будем усложнять. Обновляем контур в каждом кадре, генерируем всю верёвку и рендерим заново. Для этого нам нужен цикл анимации и способ обновления контура. Если вам незнаком цикл анимации, то можете прочитать мою статью.
Для перемещения контура я написал функцию, обновляющую координату y для каждой точки контура:
function getStepPath() {
const y = easing(t) * 100 + 50;
const y1 = y;
const y2 = 200 - y;
return M 50 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y2}</span> C 150 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y2}</span>, 150 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y1}</span>, 250 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y1}</span> C 350 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y1}</span>, 350 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y2}</span>, 450 <span class="hljs-subst" style="transition: opacity 0.2s ease-in-out 0s, color 0.2s ease-in-out 0s, text-decoration 0.2s ease-in-out 0s, background-color 0.2s ease-in-out 0s, -webkit-text-decoration 0.2s ease-in-out 0s; color: rgb(68, 68, 68); quotes: "«" "»";">${y2}</span>;
}t — это значение, постепенно меняющееся от 0 до 1 и обратно. Затем можно применить сглаживание к значению t и вычислить все значения y.
Чтобы верёвка «танцевала», нужно подключить эту логику в цикл анимации.
Я не буду вдаваться в подробности реализации, рекомендую изучить код и поэкспериментировать с ним.
Анимация

На этом всё! Наша верёвка наконец-то готова!
Мысли в заключение
На написание этого поста ушло гораздо больше времени, чем я ожидал; надеюсь, он понравился вам так же, как и мне.
Можете:
-
поэкспериментировать с интерактивным демо в оригинале статьи;
-
изучить код на CodePen;
-
просмотреть код интерактивных примеров из оригинала статьи (учтите, что код довольно грязный).
Автор:
nmgtech





