Обычно, когда мы говорим о беспилотных летательных аппаратах (БПЛА) [1], на ум сразу приходит квадрокоптер (или другой представитель класса мультикоптеров, например, гекса- или октокоптер). Но строго говоря, беспилотник не обязательно должен быть мультикоптером – он может быть выполнен в виде любой механической схемы, которая ранее была разработана для пилотируемого полёта.
Например, это может быть летательный аппарат легче воздуха, то есть аэростат (воздушный шар) или дирижабль [2]. Данной статьёй мы открываем цикл публикаций, в котором расскажем в режиме «хроник лаборатории» о ходе нашего сайд-проекта по сборке БПЛА в виде стратостата [3]. Но прежде, чем что-то собирать, нужно хорошо разобраться в предмете, в его теоретической части. Поэтому мы решили начать с того, чтобы изучить динамику вертикального полёта воздушного шара.

Ничего принципиально нового, что бы не было известно до нас, мы на этом пути, конечно же, не открыли, но такой цели перед нами и не стояло. Сайд-проект, в первую очередь, делается ради интереса, для того, чтобы разработать и сконструировать что-то самим, а не только читать о чужих достижениях. В настоящей статье мы постарались изложить доступным языком основы динамики вертикального полёта аэростата, учитывая те сложности и ошибки, с которыми столкнулись сами при изучении материала.
1. Какие силы действуют на воздушный шар
Динамика полёта воздушного шара – вещь непростая и довольно капризная, так как приходится учитывать поведение ветра, которое не очень-то предсказуемо по своей природе. Именно поэтому, чтобы не утонуть на первых же шагах в чрезмерных сложностях, мы решили упростить задачу и ограничиться рассмотрением только вертикального полёта, то есть взлёта, набора высоты, снижения и посадки.
Для начала давайте разберёмся, какие силы действуют на аэростат и почему он вообще летает (а в более общей постановке вопроса – почему он изменяет свою высоту, то поднимаясь вверх, то опускаясь вниз).
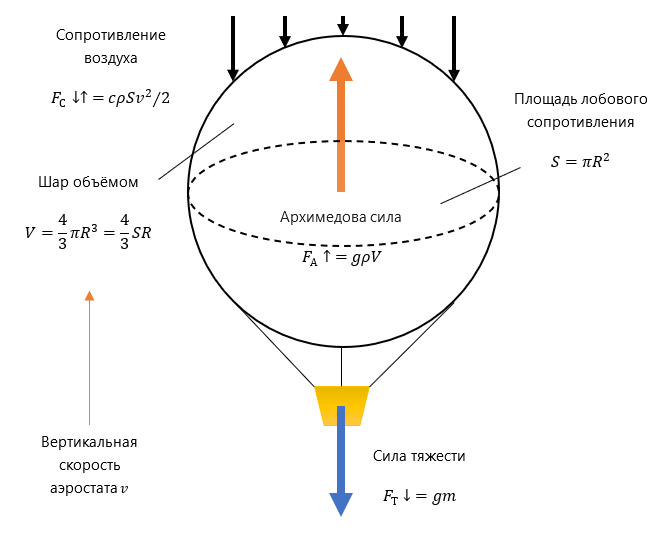
Вертикальный полёт аэростата определяется тремя силами: силой тяжести, архимедовой силой и силой сопротивления воздуха.
-
Сила тяжести
направлена всегда вниз.
-
Архимедова сила
направлена всегда вверх, и именно она заставляет аэростат подниматься. Поэтому эту силу ещё называют подъёмной.
-
Сила сопротивления воздуха
направлена против движения аэростата, то есть вниз при взлёте и наборе высоты, и вверх при снижении и посадке.
Отсюда второй закон Ньютона для шара в векторном виде будет выглядеть следующим образом:
где– ускорение [4] воздушного шара,
– его масса.
Теперь дадим пояснения по каждой из трёх сил в уравнении (1), договорившись, что положительное направления осибудет направлено вверх. Таким образом, скорость
шара положительна, если он набирает высоту (летит вверх), и отрицательна, если он снижается (летит вниз). Ускорение свободного падения
соответственно, будет отрицательным; ускорение, вызванное архимедовой силой – положительным; а ускорение, вызванное силой сопротивления воздуха, будет иметь знак, противоположный знаку скорости
.
Архимедова сила, где
– плотность внешнего воздуха (атмосферы, в которой летит наш воздушный шар), а
– это объём шара. Строго говоря, в качестве объёма
нужно брать объём всего аэростата, включая и гондолу. Но поскольку её объём существенно меньше объёма собственно шара, то есть шарообразной оболочки, наполненной газом легче воздуха, будем в качестве
, для упрощения расчётов, рассматривать только объём этой шарообразной оболочки:
где– радиус оболочки [5]. В дальнейшем нам понадобится площадь поперечного сечения шара (круга радиусом
)
. Используя это выражение мы можем записать
, откуда архимедова сила
2. Как рассчитать ускорение воздушного шара
Теперь сделаем одно алгебраическое преобразование, которое позволит нам упростить формулу (1). Представим, что вся масса аэростатасосредоточена в объёме шара (оболочки)
. Введём понятие приведённой плотности
которая показывает, какая бы плотность была у аэростата, если бы вся его масса (гондола, оболочка, газ в оболочке) была размещена внутри самой оболочки. Отсюда полную массу аэростата можно выразить как
С массой и приведённой плотностью мы разобрались, с архимедовой силой тоже. Осталось разобраться с силой сопротивления воздуха:
где– характерная площадь лобового сопротивления, а
– коэффициент сопротивления.
В нашем случае– это площадь поперечного сечения шара (круга радиусом
), которую мы уже рассмотрели выше. (Обратите ещё раз внимание:
– площадь поперечного сечения шара, а не его поверхности).
– безразмерный коэффициент сопротивления формы, который для шара равен
[W1].
– по-прежнему плотность внешнего воздуха (атмосферы), то есть среды, в которой осуществляется полёт и которая оказывает сопротивление.
– вертикальная скорость шара.
Теперь, используя (3), (5), (6), запишем компоненты уравнения (1) в алгебраическом виде:
(так как сила тяжести всегда направлена вниз)
Знакздесь показывает, что сила сопротивления воздуха
направлена вниз при подъёме шара и вверх при его спуске.
Правомерно также задать следующий вопрос: а стоит ли вообще учитывать силу сопротивления воздуха? Насколько значительный вклад она вносит в суммарное ускорение аэростата? Забегая вперёд, скажем, что да – стоит. Результаты численного моделирования, которые мы приведём в следующей статье, демонстрируют, что ускорение, создаваемое силой сопротивление воздуха, по порядку составляетот общего ускорения воздушного шара.
Выпишем теперь полное уравнение:
разделим его на (массу аэростата) и получим
Итак, мы получили уравнение, ради которого все вышеприведённые математические выкладки и затевались. Оно описывает зависимость ускорения аэростата от других кинематических характеристик (скорости), параметров конструкции аэростата (массы и объёма, «замаскированных» под приведённую плотность и радиус оболочки) и параметров внешней среды (плотности воздуха и ускорения свободного падения) [6].
В следующей статье мы расскажем о том, как решать это уравнение, чтобы получить значения высоты полёта, скорости и ускорения аэростата для заданных моментов времени.
Примечания
[1] Далее термины «беспилотный летательный аппарат», «беспилотник», «дрон» и сокращение БПЛА мы будем употреблять как синонимы.
[2] Основное отличие аэростата от дирижабля с точки зрения механики состоит в том, что дирижабль оснащён силовой установкой и может управляемо перемещаться в заданном направлении в горизонтальной плоскости, в то время как перемещения аэростата в горизонтальной плоскости носят неуправляемый характер, он летит туда, куда дует ветер.
[3] Хотя в конечном счёте проект будет посвящён сборке стратостата, начнём мы с обычного аэростата. Основное отличие между ними состоит в том, что аэростат предназначен для полётов в тропосфере (то есть на высотах до 11 км), а стратостат – в более высоких слоях атмосферы. Очень низкое атмосферное давление в высоких слоях накладывает на стратостаты дополнительные требования по прочности конструкции. Но уравнения динамики вертикального полёта аэростата и стратостата одинаковы, поэтому дальше, в целях упрощения изложения, мы везде будем использовать термин «аэростат» как более общий (стратостаты являются подклассом аэростатов) или же синонимичный ему термин «воздушный шар».
[4] В дальнейшем, когда мы будем говорить о скорости аэростата и его ускорении, мы будем иметь ввиду именно вертикальные скорость и ускорение.
[5] На самом деле (как видно, например, на фотографии), оболочка аэростата не является строго сферической, и иногда отклонение её формы от сферы может быть значительным. Однако пока мы примем допущение о сферичности оболочки для упрощения расчётов.
[6] Такие величины, как ускорение свободного падения, плотность воздуха
, объём оболочки аэростата
и его скорость
не являются постоянными.
и
убывают по мере набора высоты. Уменьшение плотности воздуха в высоких слоях атмосферы приводит к уменьшению его давления, что, как следствие, приводит к увеличению объёма оболочки аэростата. Наконец, скорость аэростата изменяется всегда, когда ускорение
. Таким образом, уравнение (9) описывает мгновенное ускорение аэростата в данный момент времени.
Ссылки
[W1] Коэффициент сопротивления формы – https://ru.wikipedia.org/wiki/Коэффициент_сопротивления_формы
Автор:
DmitryKryzhanovskiy



