
Продолжаю делиться своим опытом погружения в мир генарта и nft, на этот раз при помощи генеративных грибов. Для тех кто не совсем в теме хотя бы одного из этих слов, предлагаю сначала посмотреть мою предыдущую публикацию, а в этой статье я постараюсь больше сосредоточиться не на философии того, что вообще происходит, а на технической реализации процедурной 3д графики в three js.
На чём будем писать
Можно было бы запрогать грибы в блендере или тачдизайнере и получить (наверное) гораздо более серьёзные результаты, но так как генератор изначально задумывался именно под нфт контекст, то пришлось ограничиться javascript-ом и возможностями webgl. В качестве фреймворка для работы с 3d графикой я выбрал three.js, просто потому что это название было на слуху даже у далёкого от фронтенда меня. Вцелом, о выборе не жалею, api библиотеки оказалась довольно простым и понятным. В этой статье я не буду разбирать базовые принципы работы с three js, про них можно почитать тут.
Рисуем ножку
Начнём рисовать гриб с ножки. Не будем искать лёгких путей, а создадим 3д геометрию параметрически, прямо из точек и граней. Идея такая: возьмём гладкую кривую и станем двигать по ней некоторый замкнутый контур, порождая по мере движения точки. Дальше натянем на эти точки грани и получим искривлённый цилиндр - подобие ножки гриба. А варьируя радиус контура и его форму по ходу движения по кривой, сделаем ножку более органической и реалистичной.
Геометрия ножки
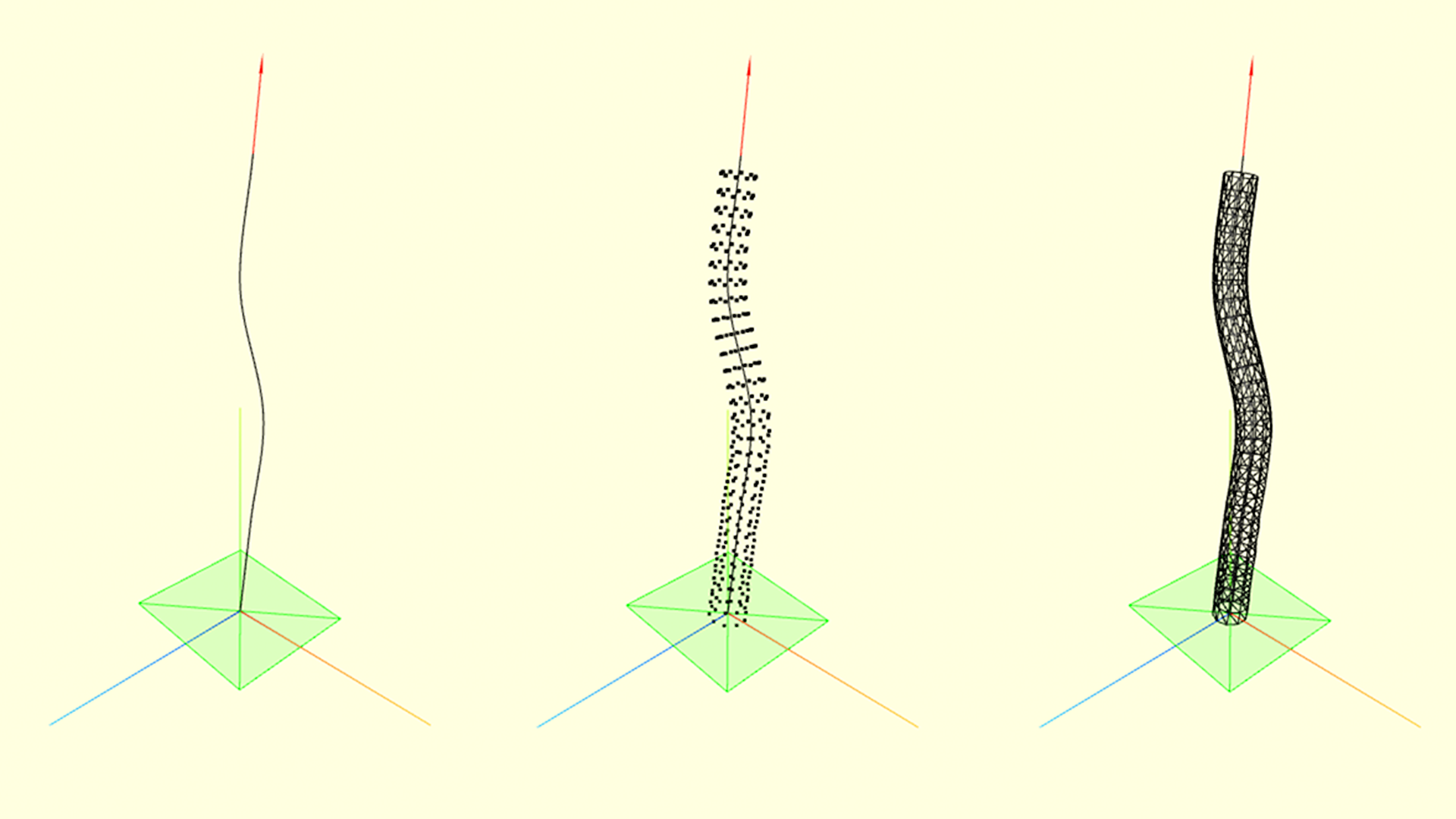
Определим форму ножки как сплайн Катмулла-Рома по нескольким рандомизированным ключевым точкам. Форма среза ножки - тоже сплайн, но замкнутый, проведённый по 4 точкам, радиус которого задаётся как функция угла и относительного положения среза на первом сплайне. При независящем от угла радиусе, этот сплайн близок к окружности и казалось бы - почему не использовать вместо него окружность? Но на самом деле, его параметризация позже пригодится нам чтобы красиво наложить шум на форму ножки гриба. Ниже - пример кода, основанный на api BufferGeometry, где создаются точки ножки гриба и индексируются её грани, а подробнее о работе с буфферной геометрией можно почитать тут.
Генерация ножки
shroom_height = 10;
stipe_vSegments = 20;
stipe_rSegments = 20;
stipe_points = [];
stipe_indices = [];
// радиус ножки, как функция угла и позиции на сплайне
function stipe_radius(a, t) {
return 1;
}
// форма ножки
stipe_shape = new THREE.CatmullRomCurve3( [
new THREE.Vector3( 0, 0, 0 ),
new THREE.Vector3( 1, shroom_height * 0.25, 0 ),
new THREE.Vector3( 2, shroom_height * 0.5, 0),
new THREE.Vector3( 0, shroom_height * 0.75, 0),
new THREE.Vector3( 1, shroom_height, 0 ),
], closed=false );
// t - относительное положение среза на stipe_shape, от 0 до 1
for (var t = 0; t < 1; t += 1 / stipe_vSegments) {
// форма среза ножки
var curve = new THREE.CatmullRomCurve3( [
new THREE.Vector3( 0, 0, stipe_radius(0, t)),
new THREE.Vector3( stipe_radius(Math.PI / 2, t), 0, 0 ),
new THREE.Vector3( 0, 0, -stipe_radius(Math.PI, t)),
new THREE.Vector3( -stipe_radius(Math.PI * 1.5, t), 0, 0 ),
], closed=true, curveType='catmullrom', tension=0.75);
// вычисляем точки на срезе ножки
var local_points = curve.getPoints( stipe_rSegments );
// добавляем точки к мешу
for (var i = 0; i < local_points.length; i++) {
var v = local_points[i];
stipe_points.push(v.x, v.y, v.z);
}
}
// задаём индексы точек, образующих грани, по 2 треугольника на грань
for (var i = 0; i < stipe_vSegments - 1; i ++) {
for (var j = 0; j < stipe_rSegments; j ++) {
stipe_indices.push(i * (stipe_rSegments + 1) + j,
i * (stipe_rSegments + 1) + j + 1,
(i + 1) * (stipe_rSegments + 1) + j);
stipe_indices.push(i * (stipe_rSegments + 1) + j + 1,
(i + 1) * (stipe_rSegments + 1) + j + 1,
(i + 1) * (stipe_rSegments + 1) + j);
}
}
// создаём буферную геометрию из точек и индексов граней
var stipe = new THREE.BufferGeometry();
stipe.setAttribute('position', new THREE.BufferAttribute(new Float32Array(stipe_points), 3));
stipe.setIndex(stipe_indices);
stipe.computeVertexNormals();Шумы
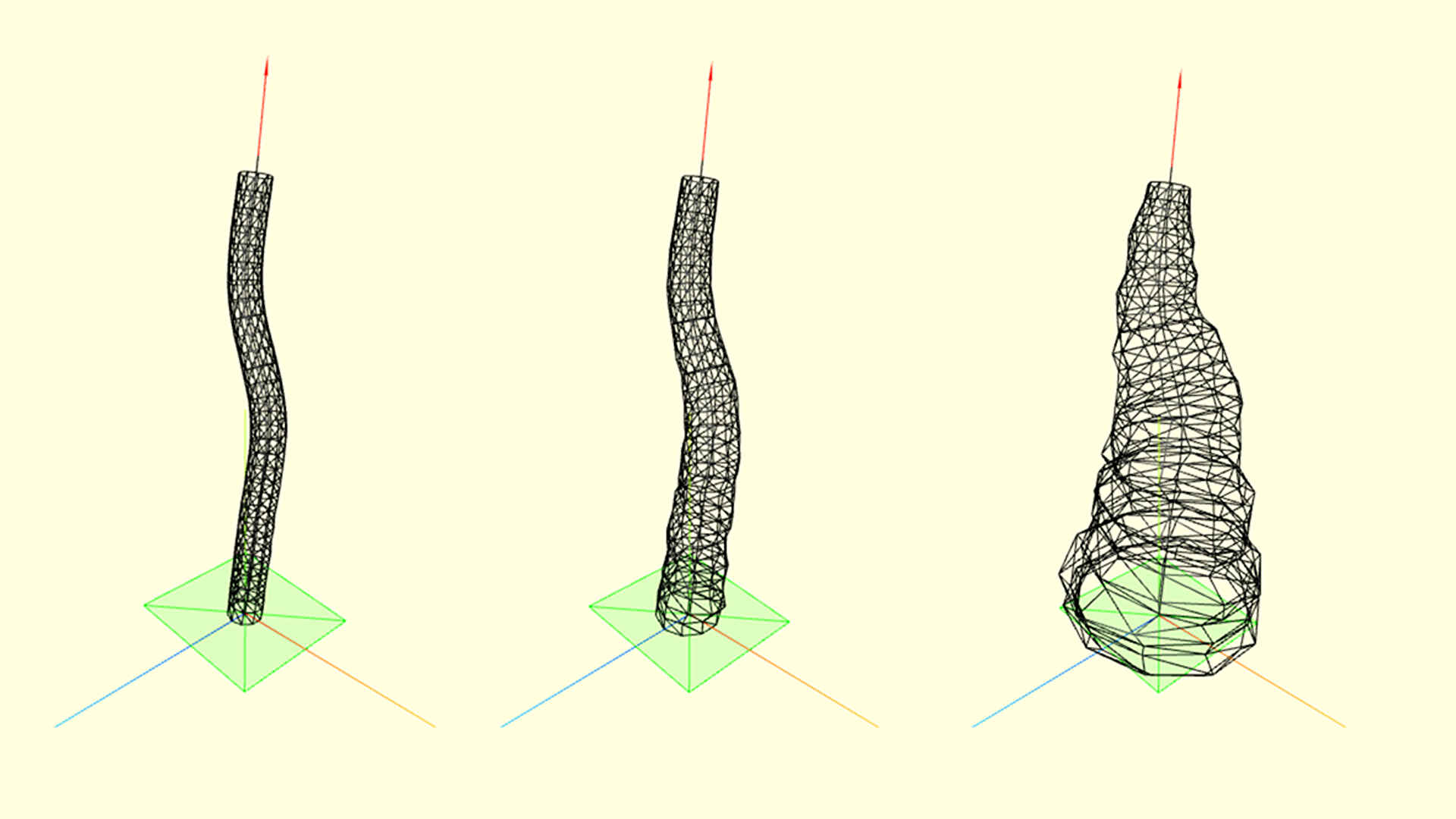
Чтобы ножка выглядела более реалистично, можно добавить шума в функцию, вычисляющую её радиус. На рисунке - примеры того как радиальный шум из фрагмента кода ниже влияет на форму ножки в зависимости от коэффициента noise_c. Зашумление радиуса при этом зависит от высоты точки на ножке, чем выше - тем более гладкой становится поверхность ножки.
Параметризация и зашумление радиуса ножки
base_radius = 1;
noise_c = 2;
// радиус ножки, как функция угла и позиции на сплайне
function stipe_radius(a, t) {
return base_radius + (1 - t)*(1 + Math.random())*noise_c;
}Рисуем шляпку
Геометрия шляпки
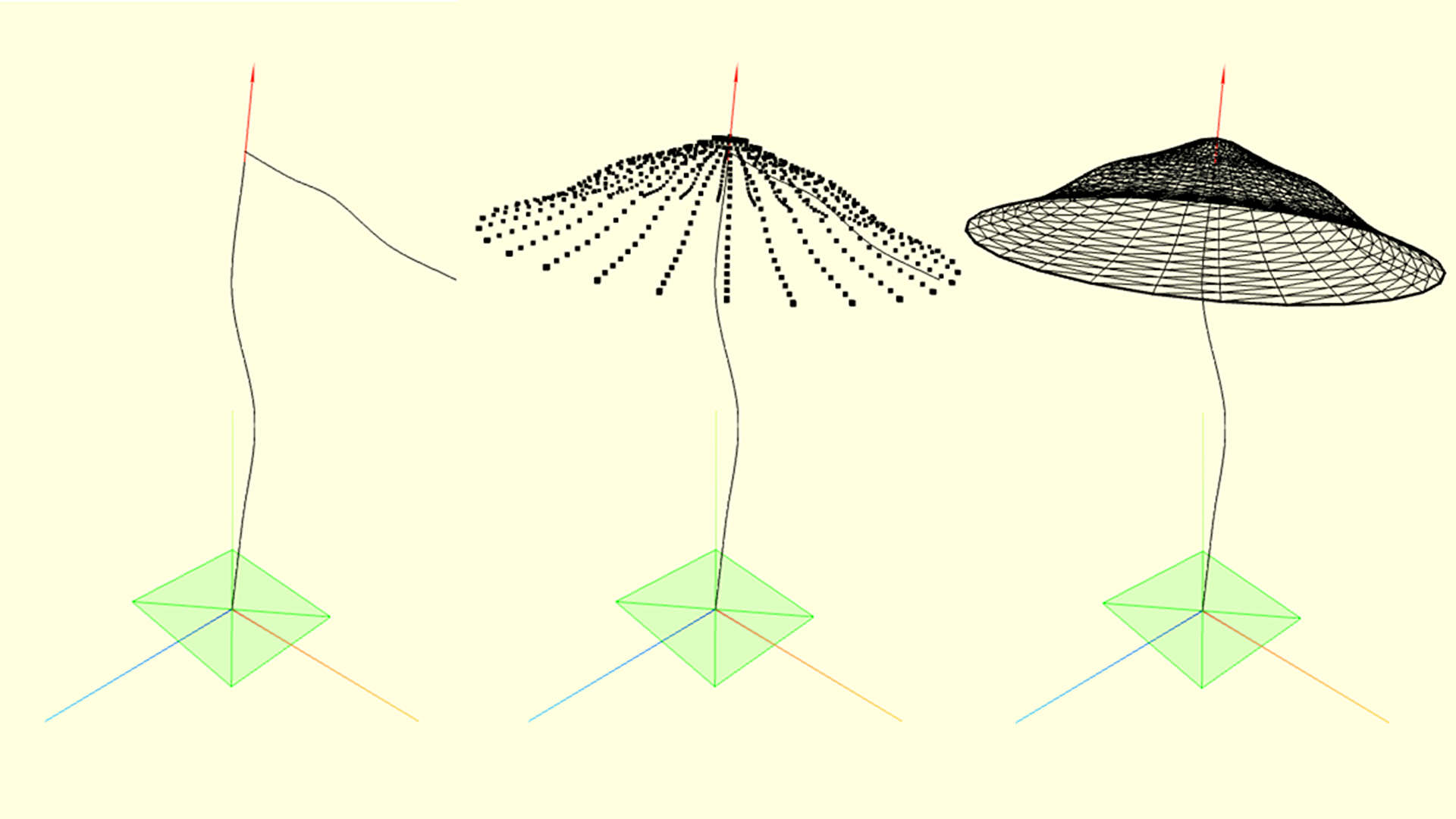
Аналогично ножке, из точек и граней будем генерировать шляпку. Пусть срез шляпки описывается некоторым сплайном (см. левый рисунок). Будем вращать этот сплайн вокруг конца стебля, порождая точки и объединяя их гранями.
Генерация шляпки
pileus_points = [];
pileus_indices = [];
// точка поверхности шляпки как функция радиальных координат
function pileus_surface(a0, t0) {
// вычисляем относительное положение точки
// на кривой с учётом возможного радиального шума
var t = t * (1 + radnoise(a, t));
// проверка того что мы не вышли за кривую
if (t > 1) t = 1; if (t < 0) t = 0;
// вычисляем нормаль, ортогональную поверхности
// в данной точке (единичный вектор ортогонального шума)
var shape_point = pileus_shape.getPointAt(t);
var tangent = pileus_shape.getTangentAt(t);
var orth_noise_v = new THREE.Vector3(0,0,0);
const z1 = new THREE.Vector3(0,0,1);
orth_noise_v.crossVectors(z1, tangent);
// вычисляем значение угла с учётом углового шума и
// положение точки с учётом обновлённого угла
var a = angnoise(a0, t);
var surface_point = new THREE.Vector3(
Math.cos(a) * shape_point.x,
shape_point.y,
Math.sin(a) * shape_point.x
);
// вычисляем множитель ортогонального шума
var surfnoise_val = orthnoise(a, t);
// финальные координаты точки (a0, t0) с учётом всех шумов
surface_point.x += orth_noise_v.x * Math.cos(a) * surfnoise_val;
surface_point.y += orth_noise_v.y * surfnoise_val;
surface_point.z += orth_noise_v.x * Math.sin(a) * surfnoise_val;
return surface_point;
}
// формируем поверхность шляпки с разрешением
// pileus_rSegments * pileus_cSegments
for (var i = 1; i <= pileus_rSegments; i++) {
var t0 = i / pileus_rSegments;
for (var j = 0; j < pileus_cSegments; j++) {
var a0 = Math.PI * 2 / pileus_cSegments * j;
var surface_point = pileus_surface(a0, t0);
pileus_points.push(
surface_point.x,
surface_point.y,
surface_point.z
);
}
}
// индексная магия, соединяющая точки гранями
for (var i = 0; i < pileus_rSegments - 1; i ++) {
if (i == 0) {
for (var j = 0; j < pileus_cSegments; j ++)
pileus_indices.push(
0,
(j + 1) % pileus_cSegments + 1,
j + 1
);
}
for (var j = 0; j < pileus_cSegments; j ++) {
pileus_indices.push(
i * pileus_cSegments + 1 + j,
(i + 1) * pileus_cSegments + 1 + (j + 1) % pileus_cSegments,
(i + 1) * pileus_cSegments + 1 + j
);
pileus_indices.push(
i * pileus_cSegments + 1 + j,
i * pileus_cSegments + 1 + (j + 1) % pileus_cSegments,
(i + 1) * pileus_cSegments + 1 + (j + 1) % pileus_cSegments
);
}
}
// объединяем всё что нагенерили в буфферную геометрию
pileus.setAttribute('position', new THREE.BufferAttribute(new Float32Array(pileus_points), 3));
pileus.setIndex(pileus_indices);
pileus.computeVertexNormals();Шумы
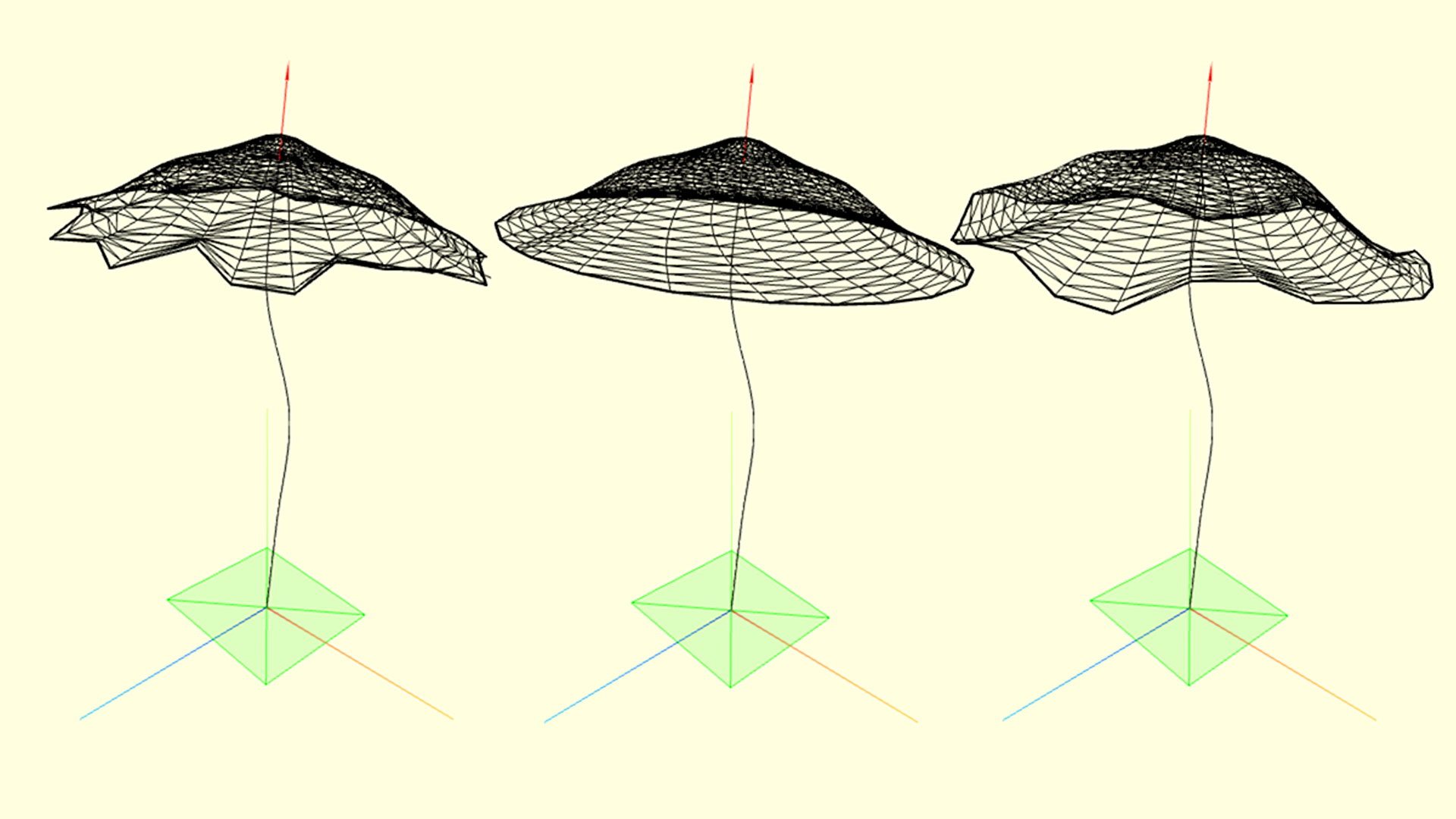
Теперь наложим на шляпку шумы, чтобы сделать её форму реалистичнее. В своём коде я разделил шум шляпки на 3 составляющие: радиальный - вариация радиуса шляпки в зависимости от угла, угловой - искажение угла как функция от угла, и ортогональный - сдвиг координаты точки в направлении вектора, ортогонального изначальному сплайну шляпки в этой точке. Так как шляпка задаётся радиальными координатами, для получения красивых изгибов здесь удобно применить некоторый шум, являющийся непрерывной функцией координат, например 2d шум Перлина. Для этого я использовал библиотеку noisejs.
Шляпный шум
NOISE.seed(Math.random());
function radnoise(a, t) {
return -Math.abs(NOISE.perlin2(t * Math.cos(a), t * Math.sin(a)) * 0.5);
}
function angnoise(a, t) {
return NOISE.perlin2(t * Math.cos(a), t * Math.sin(a)) * 0.2;
}
function orthnoise(a, t) {
return NOISE.perlin2(t * Math.cos(a), t * Math.sin(a)) * t;
}Пластинки, юбка, точки на шляпке
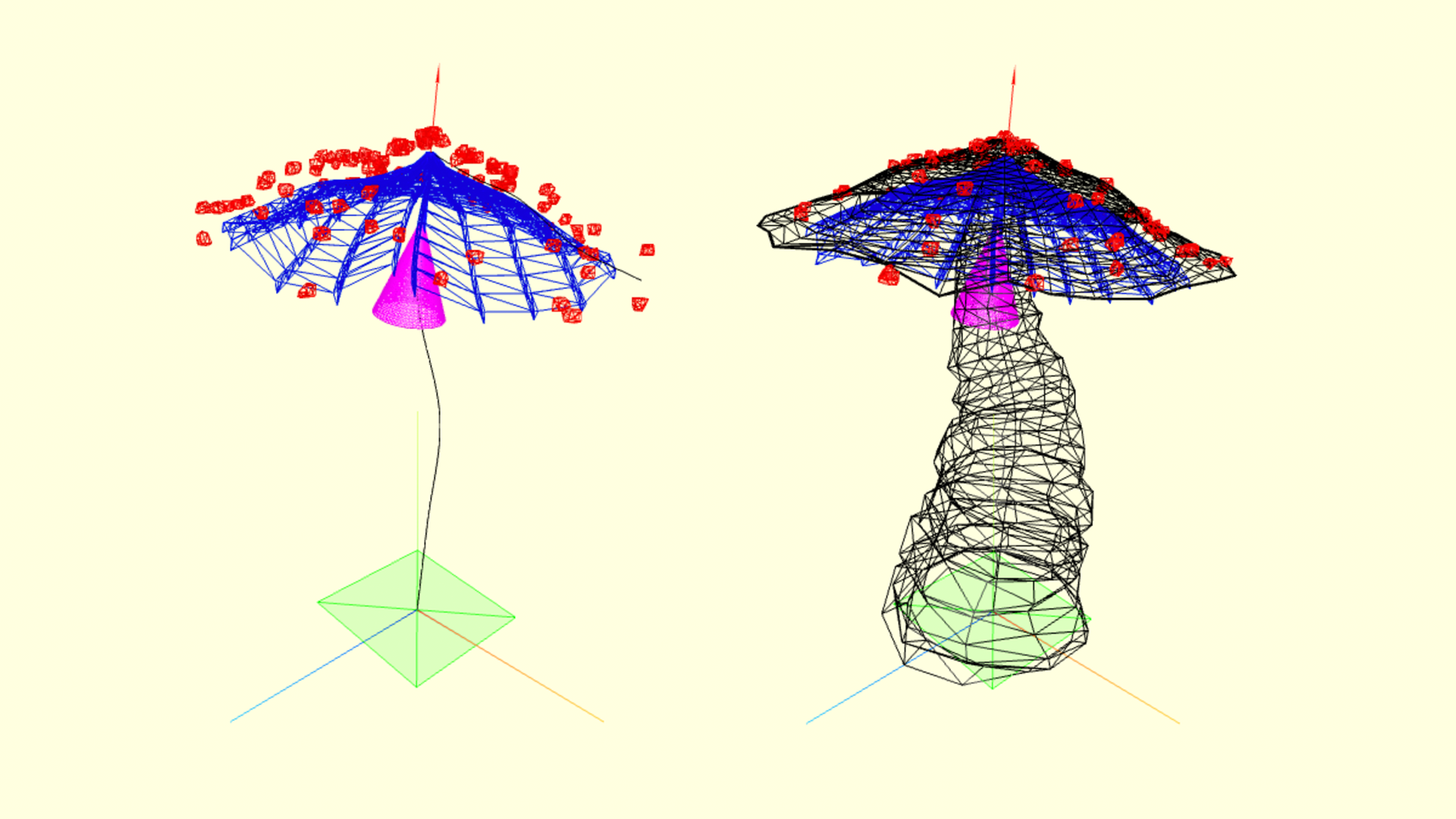
По аналогии со шляпкой можно сгенерировать и ещё 2 узнаваемых части гриба - пластинки и юбку. А чтобы нарисовать точки на шляпке (как у мухомора), будем генерировать случайные облака точек и строить по ним замкнутую геометрию методом ConvexGeometry, а потом объединим их все в одну буфферную геометрию через mergeBufferGeometries.
Генерация мухоморных точек
var bufgeoms = [];
var N = 10;
for (var i = 0; i < dots_num; i++) {
var dot_points = [];
// выбираем случайный центр точки на шляпке
var a = Math.random() * Math.PI * 2;
var t = Math.random();
var dot_center = pileus_surface(a, t);
// генерируем случайное облако точек вокруг центра
for (var j = 0; j < N; j++) {
dot_points.push(new THREE.Vector3(
dot_center.x + (1 - Math.random() * 2) * dot_radius,
dot_center.y + (1 - Math.random() * 2) * dot_radius,
dot_center.z + (1 - Math.random() * 2) * dot_radius
);
}
// создаём замкнутую геометрию на основе облака точек
var dot_geometry = new THREE.ConvexGeometry( dots_points );
bufgeoms.push(dots_geometry);
}
// объединяем все мухоморные точки в одну буфферную геометрию
var dots = THREE.BufferGeometryUtils.mergeBufferGeometries(bufgeoms);Проверка коллизий
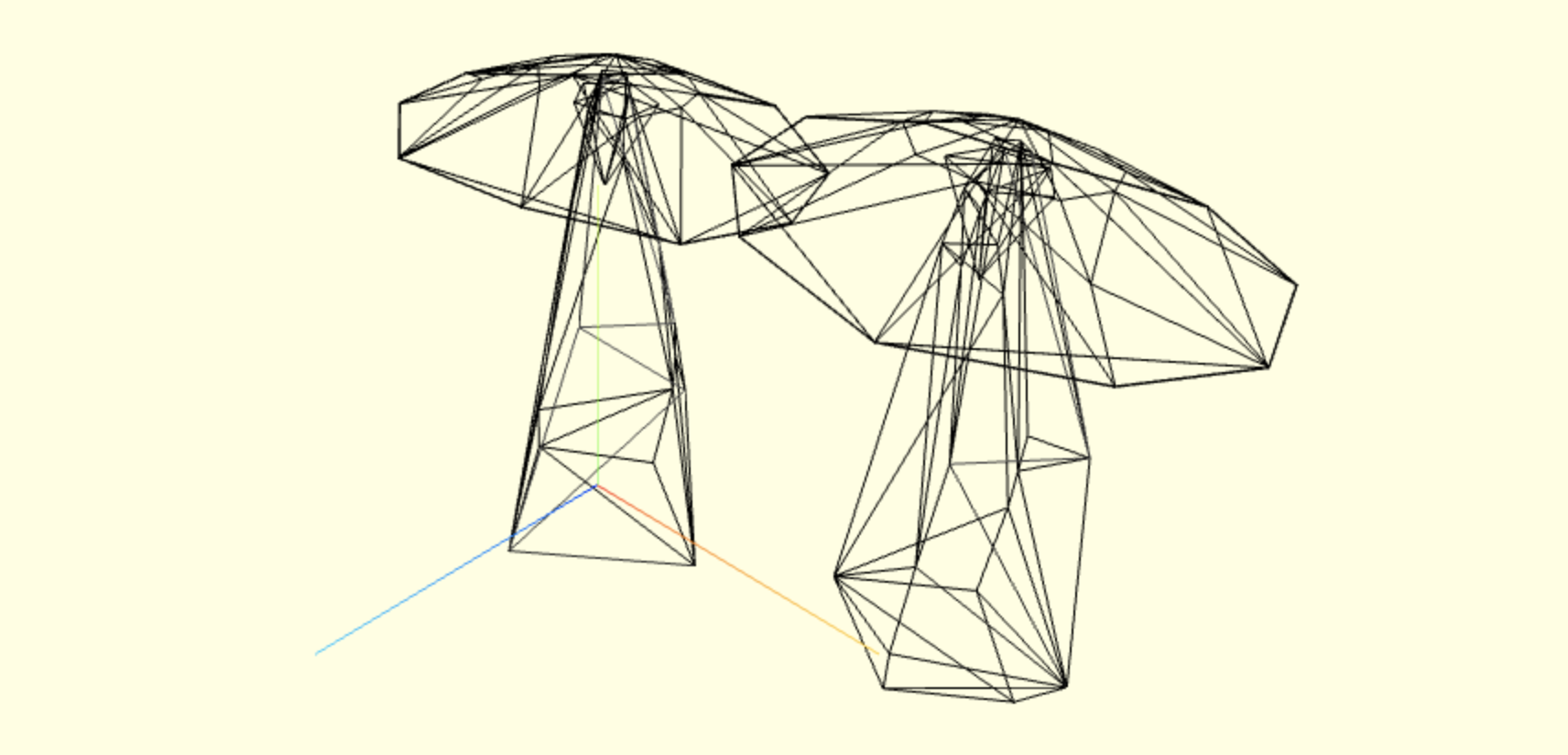
Один гриб хорошо, а много - лучше. Но если размещать случайные грибы случайным образом в пространстве, то они рано или поздно начнут пересекаться друг с другом разными невозможными способами. Чтобы так не происходило, я честно спёр вот отсюда сниппет проверяющий коллизии объектов друг с другом. А чтобы проверка коллизий не занимала слишком много времени - вместе с основным грибом я генерирую его упрощённую модель с малым количеством вертексов.
Генерация названий
Для генерации названий грибов я использовал самописную цепь маркова обученную на тысяче названий реальных видов грибов вот отсюда. Первым делом надо было разбить обучающие тексты на некоторое количество общих токенов, из которых потом будет формироваться генеративный текст. Я использовал токенизатор YouTokenMe, разбил названия на 200 токенов и посчитал вероятности их перехода друг в друга и записал получившуюся матрицу вероятностей переходов в json. Всё что делает JS код - это просто считывает эту матрицу и случайным образом выбирает следующий токен на основе вероятностей переходов из предыдущего пока не накопится несколько слов.
Рендеринг и стилизация
Обводка контура
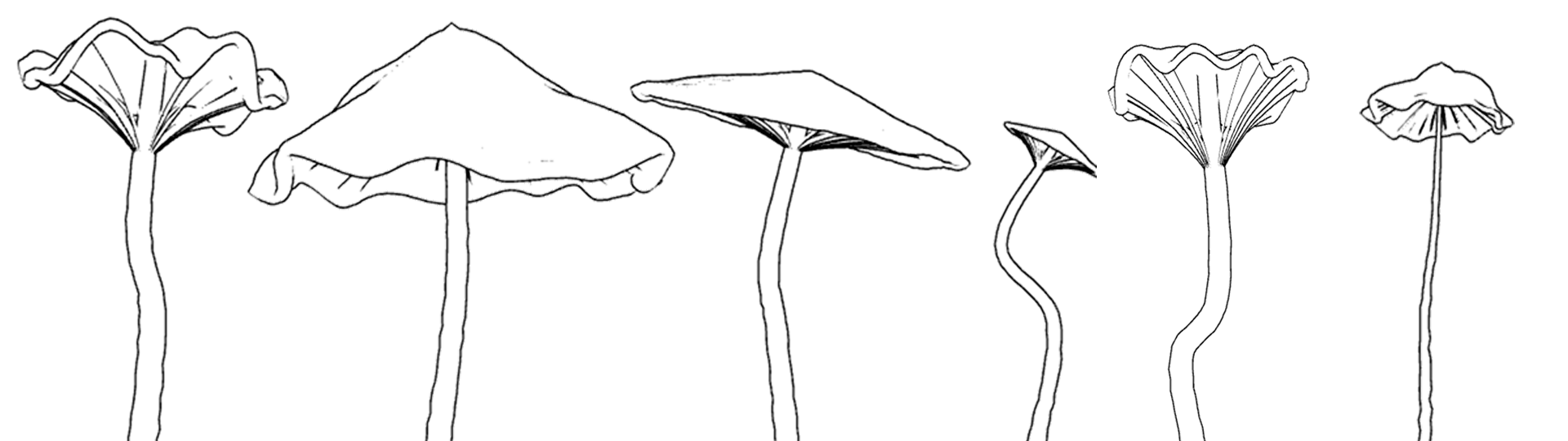
Для получения эффекта обводки я использовал OutlineEffect вот отсюда. Вместе с белой текстурой и отсутствием теней, такие контуры дают прикольный скетчевый эффект.
Цвет
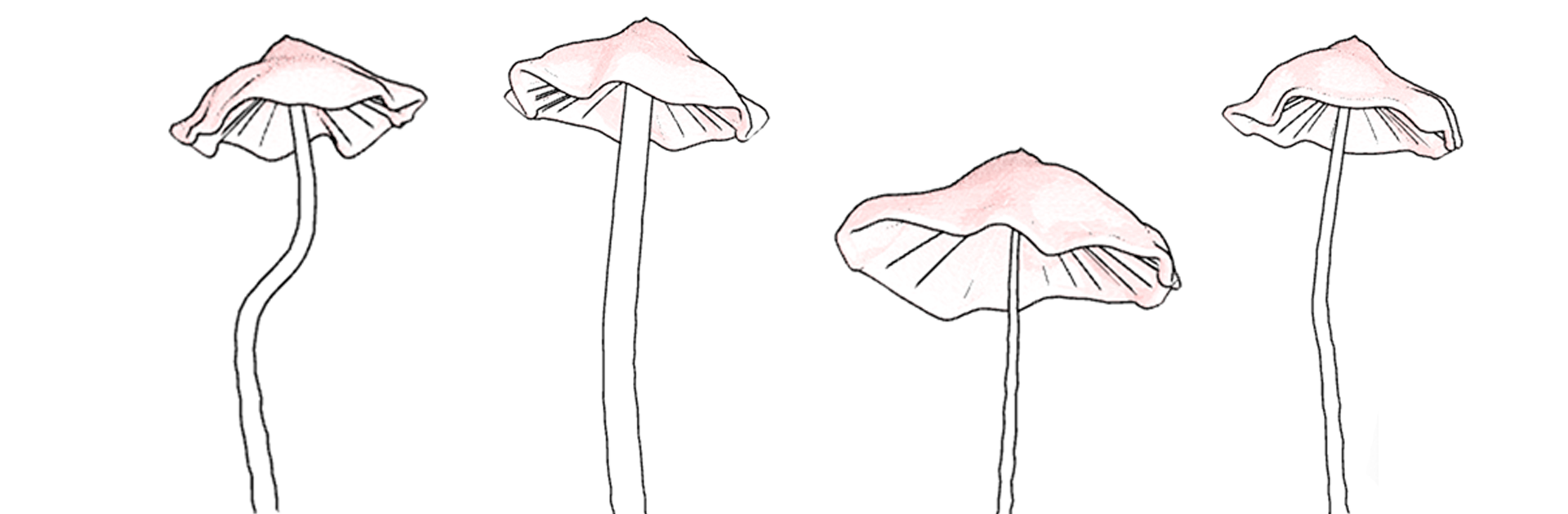
Но хотелось цвета, а генерировать ещё и UV-map не хотелось. Тут очень кстати пришлась возможность задать цвета вертексов буферной геометрии. Точно так же как и шумы геометрии, цвет вертекса можно параметризовать как функцию угла и относительного положения точки на базовом сплайне. В качестве примера, добавим несколько строк, красящих вертексы в код генерации ножки.
Красим ножку
stipe_colors = [];
c = [100, 100, 100] // базовый цвет
v = [100, 100, 100] // диапазоны вариации цвета
function stipe_color(a, t) {
return [c[0] + t * v[0], c[1] + t * v[1], c[2] + t * v[2]];
}
...
stipe_points.push(v.x, v.y, v.z);
stipe_colors.push(...stipe_color(a, t));
...
var stipe = new THREE.BufferGeometry();
...
stipe.setAttribute('color', new THREE.Float32BufferAttribute(stipe_colors, 3));"Плёночный" шум
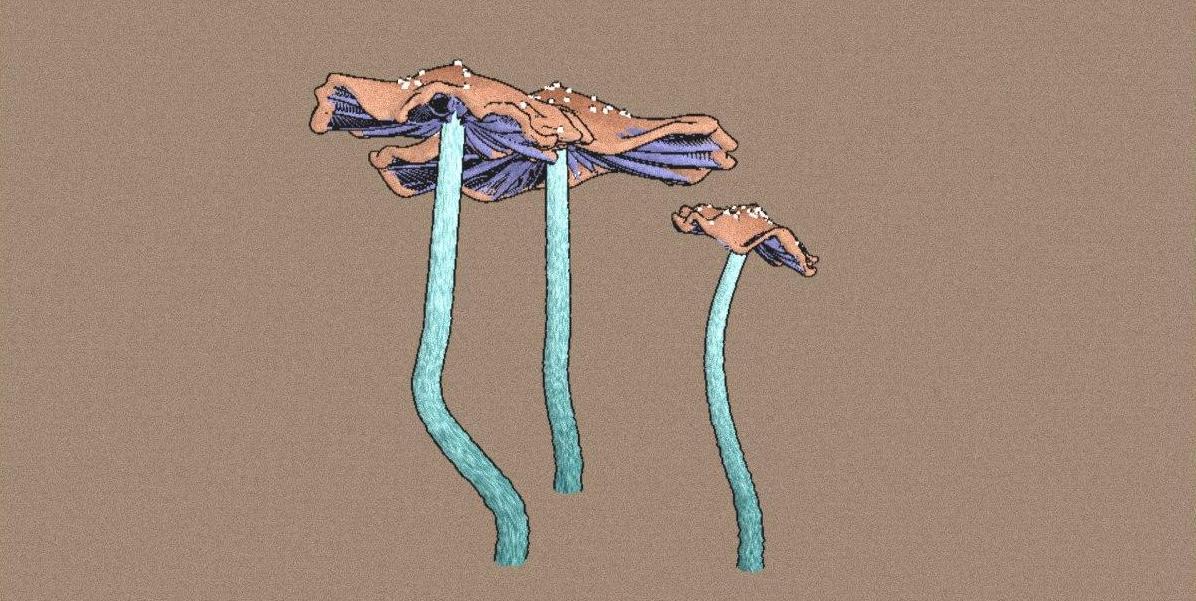
Так как я не сильно шарю в шейдерах, для зашумления итоговой картинки я использовал EffectComposer - штуку, сильно облегчающую постпроцессинг в three js. Как ей пользоваться можно посмотреть например тут. Для неё уже написано много эффектов, в том числе и нужный мне шум.
Итоги

В итоге у меня получился генератор волшебных грибов, работающий в браузере. Потыкать грибы и посмотреть на их вариации можно на платформе fxhash.
Ссылки
Three js - официальная документация по three js
Генклуб - русскоязычное сообщество любителей генарта
Twitter - мой твиттор вот с этими всеми генеративными штуками
Автор: Ilya Belikov





