Статистический подход к объяснению ошибочных дедлайнов в инженерных проектах

Кем бы вы ни были — джуниором, сениором, менеджером проекта или менеджером верхнего звена с двадцатилетним опытом — оценка времени проекта разработки ПО никогда не бывает простой задачей. Никто, вне зависимости от его опыта и гениальности, не может утверждать, что знает точное время завершения программного проекта.
Эта проблема особенно актуальна в проектировании ПО, но и в другие инженерные дисциплины страдают от того же. Поэтому хотя в этой статье говорится о проектировании ПО, она в некоторой степени относится и к другим дисциплинам.
Общая информация
Давайте сначала взглянем на проблему, её последствия и потенциальные первопричины с высоты птичьего полёта.
Проблема
Программные проекты редко укладываются в дедлайн.
Последствия
Растрата затрат на маркетинг, разочарование клиентов, измотанные разработчики, пищущие низкокачественный код, чтобы уложиться в дедлайны ценой снижения надёжности продукта, а в конечном итоге — вероятное прекращение проекта.
Известные причины
- Неправильная оценка времени (основная тема этой статьи).
- Нечётко сформулированные на старте проекта требования с их последующим изменением.
- Украшательства: слишком много внимания уделяется деталям, не относящимся к сути проекта.
- Недостаточно времени уделено этапу исследований и проектирования архитектуры. Или наоборот — уделено слишком много времени.
- Недооценка потенциальных проблем интеграции со сторонними системами.
- Стремление «сделать всё правильно с первого раза»
- Параллельная работа над слишком большим количеством проектов или отвлечение (слишком частое прерывание потока).
- Несбалансированное соотношение качества и производительности.
Чрезмерный оптимизм, эффект Даннинга-Крюгера, чистая неопределённость или просто математика?

Пятая стадия: ПРИНЯТИЕ.
Сразу можно отбросить чрезмерный оптимизм — логично, что ни один разработчик, когда-либо испытывавший проблемы с дедлайнами, не будет оптимистичен при их выборе. Если же руководство проекта не имеет инженерного опыта и не понимает, что делает, то это тема для совершенно другой статьи.
Некоторые связывают ошибочные временные оценки с эффектом Даннинга-Крюгера, однако если недооценка времени связана с недостатком опыта или переоценкой своих способностей, то получение опыта должно определённо решить проблему, не так ли? Однако даже самые крупные компании с практически бесконечными ресурсами всё равно имеют на удивление высокие показатели пропущенных дедлайнов, поэтому эта гипотеза опровергнута. Не говоря уже о том, что все мы испытывали это на себе. Наличие большего опыта почти не помогает в оценке времени.
Многие разработчики, особенно наиболее опытные из них, быстро приходят к выводу, что дело исключительно в неопределённости. Следовательно, оценки времени всегда будут ошибочными и это просто жизненный факт. Единственное, что мы можем с этим сделать — постараться удовлетворить требования клиента и попросить разработчиков «просто кранчить», когда всё пойдёт наперекосяк. Все мы знакомы со стрессом, мусорным кодом и совершенным хаосом, создаваемыми такой философией.
Существует ли в этом безумии методика? На самом ли деле это самый лучший способ решения задач? Я не думаю, что это так, поэтому решил отправиться на поиски рационального математического объяснения тому, почему все эти умные люди не могут оценить время, которое понадобится им на выполнение работы.
Это просто математика!

Однажды я выполнял задачу, которая должна была занять 10 минут, но в конечном итоге потребовала 2 часа. Я начал размышлять о том, почему решил, что она должна занять 10 минут, и как это число выросло до 2 часов. Мой мыслительный процесс был довольно интересным:
- Я считал, что это займёт 10 минут, потому что в голове на 100% знал код, который нужно написать.
- Написание кода и в самом деле потребовало примерно 7–10 минут. А потом потребовалось 2 часа из-за совершенно неизвестного мне бага во фреймворке.
В управлении проектами подобное любят называть «форс-мажором» — внешними неконтролируемыми причинами задержки.
Вероятно, вы сейчас думаете, что этим примером я подтвердил аргумент о неопределённости планирования. На самом деле, и да, и нет. Давайте взглянем чуть издалека. Да, действительно, неопределённость стала корневой причиной задержки этой конкретной задачи, потому что я бы ни за что не догадался, что такой баг существует. Но должна ли она отвечать за задержку всего проекта?
Здесь нам нужно провести границу между одиночной задачей, нерепрезентативной для всего процесса, и наоборот.
Как мы оцениваем время в «нормальных» условиях
Нормальное распределение (гауссиана)
Нормальные распределения встречаются повсеместно и человеческий хорошо с ними освоился. Мы специалисты в оценке процессов, по своей природе следующих нормальному распределению; это основа получения знаний из опыта.
Если в этом месяце вы ходили в ближайший магазин почти 20 раз и каждый раз путь занимал 5 минут, за исключением случая, когда сломался лифт и вам пришлось прождать 10 минут, а ещё того случая, когда вы решили подождать две минуты, пока закончится дождь. Сколько по вашим оценкам понадобится времени, чтобы добраться до магазина прямо сейчас? 5 минут?
Я имею в виду, что не имеет смысла говорить «15 минут», потому что это редкий случай, или «7 минут», если только на улице нет дождя. И с большой вероятностью вы окажетесь правы. Если в 18 из 20 случаев путь занимал 5 минут, то определённо существует высокая вероятность, что он займёт 5 минут (медиана) и на этот раз. Вероятность примерно равна 90% (если, разумеется, не вдаваться в более сложные вычисления).
Но график искажён!
Даже если вы хорошо умеете оценивать время на выполнение задачи, это не значит, что вы хорошо оцените время на завершение проекта! Это контринтуитивно, но вы можете ошибиться сильнее.
Все читающие статью нерды-математики (и дата-саентисты/статистики) уже должны были узнать в крошечном графике из предыдущего мема скошенное вправо нормальное распределение. Увеличим его и объясним, что оно означает:
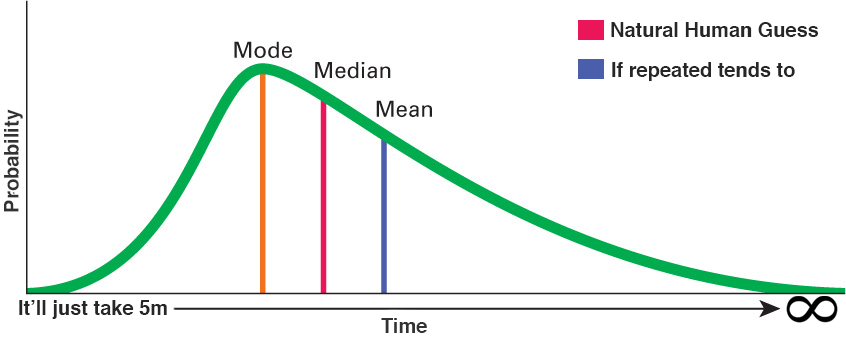
Для этой отдельной задачи медиана (median) по-прежнему имеет более высокую вероятность, чем среднее (mean)! Если вы попытаетесь угадать значение моды (mode), имеющей наивысшую вероятность, то при увеличении объёма задачи ошибётесь ещё сильнее
Видите, что здесь может пойти не так? Наша «естественная» догадка основана на медиане, максимизирующей вероятность правильной догадки, однако реальное число при выполнении «события» достаточное количество раз всегда будет стремиться к среднему. Другими словами: чем больше похожих задач вы выполняете, тем сильнее накапливается эта погрешность!
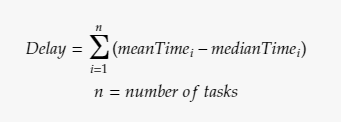
Уравнение задержки на основании этой гипотезы
Задачи программирования в проекте обычно довольно похожи друг на друга или, по крайней мере, сгруппированы в несколько похожих кластеров! Из этого уравнения также следует, что эта проблема масштабируема! Хоть мы и хотим, чтобы всё в программных проектах было масштабируемым, проблемы явно не приветствуются.
Как же воспользоваться этим знанием?
Честно говоря, в процессе написания статьи я не планировал давать «рекомендаций» на основании этой гипотезы. Она должна была стать просто объяснительным анализом, завершающимся гипотезой, интерпретировать которую читатель должен по собственному желанию.
Однако я понимаю, что многие будут разочарованы такой незавершённостью, поэтому расскажу, что из этого вынес лично я.
- Проще сказать, займёт ли задача X больше/меньше/столько же времени по сравнению с задачей Y, чем точно определить, сколько займёт их выполнение. Так получается, потому что если скошенность кривых приблизительно одинакова (что справедливо для похожих задач), то сравнение медиан даёт примерно такие же результаты, как и сравнение средних.
- Я не запоминаю и не записываю каждую отдельную задачу, чтобы проводить вычисления и получать среднее (и не могу найти никаких данных для таких опытов). Поэтому я обычно оцениваю неизбежную погрешность (среднее-медиана) как процент от времени на задачу, который увеличивается/уменьшается в зависимости от того, насколько я освоился со средой разработки. (Нравится ли мне этот язык/фреймворк (40%) Есть ли у меня хорошие инструменты отладки? (30%) Хороша ли поддержка IDE? (25%) … и т.д.).
- Я начал разделять спринты на задачи равного размера чтобы обеспечить некую однородность процесса оценки времени. Это позволяет мне воспользоваться пунктом 1. Бывает легко определить, что две задачи примерно равны по времени. Кроме того, это делает задачи ещё более похожими на то, к чему применима гипотеза, и всё становится более предсказуемым.
- Применив эти принципы, при наличии ресурсов можно организовать «тестовый прогон». Например, если за X1 дней Y1 разработчиков выполнило Z1 однородных задач, то мы можем вычислить X2 (дней), зная Y2 (количество имеющихся разработчиков) и Z2 (общее количество оставшихся задач).
На правах рекламы
Эпичные серверы для разработчиков и не только! Недорогие VDS на базе новейших процессоров AMD EPYC и NVMe хранилища для размещения проектов любой сложности, от корпоративных сетей и игровых проектов до лендингов и VPN.
Автор: Mikhail







