Уточнение погрешностей — физические константы в настоящей и новой версиях Международной системы единиц (СИ)

2019-05-09 в 20:29, admin, рубрики: Без рубрики

29 марта 2019 года — Майкл Тротт, главный научный сотрудник

— Вступление
— Мир обсуждает грядущие перемены
— Краткий обзор соответствующих ингредиентов языка Wolfram Language
— Вернемся к письму редактору
— Вычисление таблицы форм, оптимизированных по погрешности

Вступление

В так называемой «новой СИ» — обновленной версии Международной системы единиц, которая будет определять семь основных единиц измерения (секунда, метр, килограмм, ампер, кельвин, моль и кандела) и которая вступит в силу 20 мая 2019, все единицы измерения СИ будут определятся через точные значения фундаментальных физических постоянных. Как результат, все названные единицы СИ (ньютон, вольт, ом, паскаль и т. д.) будут, в конечном итоге, выражаться через фундаментальные константы. (Наконец-то, фундаментальная физика будет буквально управлять нашей повседневной жизнью ☺)

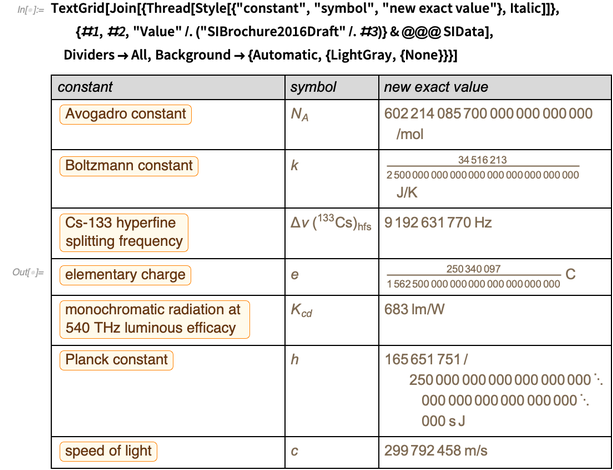
В представленной таблице демонстрируется как все изменится с вечера понедельника 20 мая до утра вторника 21 мая этого года.

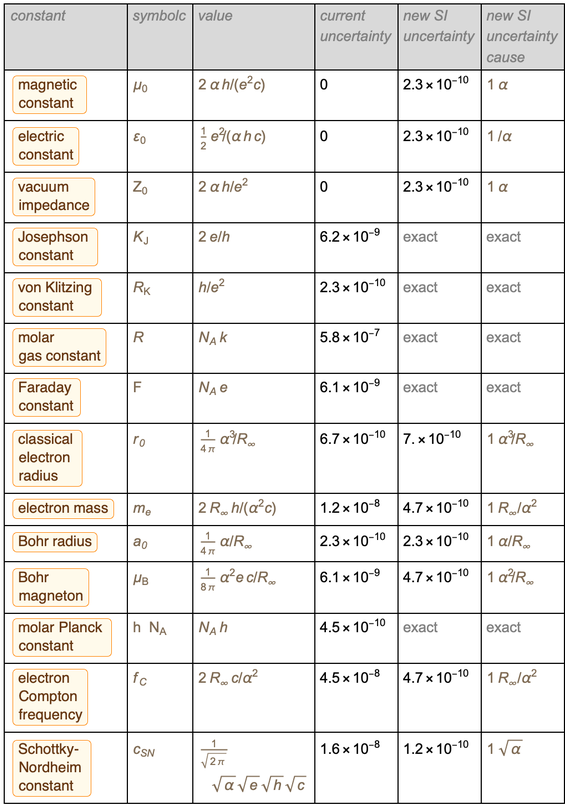
Вычисление данных из этой таблицы является целью этого блога. Итак, начнем с краткого обзора того, что изменится в новой СИ.

Помимо общеизвестного точного значения скорости света, через несколько недель еще четыре физических константы — постоянная Планка, постоянная Больцмана, постоянная Авогадро и постоянная Милликана (чаще называемая элементарным электрическим зарядом) — будут иметь точные значения. Решение об этом изменении было принято на международном уровне в ноябре прошлого года (я написал об этом в своем последнем блоге).

Ниже представлен фрагмент страницы 12 текущего проекта брошюры СИ.

Обратите внимание, что в этих определениях десятичные числа подразумеваются как точные десятичные числа, а не, скажем, машинные числа на компьютере, которые имеют конечную точность и не являются точными числами. Частота перехода в расщеплённой сверхтонкой структуре Cs-133, скорость света и «световая эффективность» уже сегодня имеют точные значения.

Мир обсуждает грядущие перемены

Это изменение будет иметь некоторые интересные последствия для других физических постоянных: некоторые константы, которые в настоящее время измеряются и имеют значения с погрешностями, станут точными, а некоторые константы, которые в настоящее время имеют точные значения, в будущем будут иметь приблизительные значения с конечными погрешностями. Эти изменения неизбежны, чтобы гарантировать общую согласованность системы.

В первом выпуске «Физики мира» этого года в письме к редактору от Уильяма Гофа затрагивалась эта тема; он написал:

С фиксацией заряда на электроне (e) и постоянной Планка (h) все физические единицы теперь «увековечены в камне», что очень приятно. Но это поднимает один неловкий вопрос. Постоянная тонкой структуры 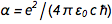, где c это скорость света и 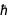это 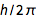. Из знакомых уравнени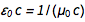й и 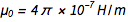мы быстро находим что 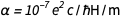. Это, конечно, чистое число с безразмерной величиной, и оно теперь навечно зафиксировано как равным 1/137.13601, что очень близко к принятому значению. Это не удивительно, так как последнее значение было бы использовано в согласованных новых значениях для e и ℏ. Но у природы есть своя ценность, неизвестная нам в настоящее время, которая из-за этого увековечена в алмазе. Мы можем быть прощены за то, что намекаем на то, что знаем лучше природы. Но что, если будущая теория вселенной станет принятой, и даст точное значение 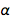, которое значительно отличается от принятого значения? Может ли такое случиться? Были попытки найти теоретическое значение для α, но они включают угрожающую и спорную квантовую электродинамику.

Проблема в том, что в новой системе СИ оба 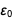и 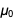теперь будут иметь неточные значения с некоторой погрешностью. В этом блоге мы будем использовать язык Wolfram Language и его знания о физических единицах и константах, чтобы увидеть, как эти и другие физические константы приобретают (или теряют) погрешность, и почему это является математическим следствием определения основных единиц.

Краткий обзор соответствующих ингредиентов языка Wolfram Language

Язык Wolfram Language — это уникальная среда для проведения численных экспериментов и символических вычислений, выявляя возможные последствия. В дополнение к общим вычислительным возможностям, здесь очень полезны три компонента системы:

1) Единицы языка Wolfram Language и структура физических величин.

«Классические» единицы (такие как метры, футы и т. д.) могут быть использованы в вычислениях и визуализациях. И, конечно же, в переводе единиц измерения.

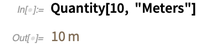
Преобразование в обычные единицы США приводит к дроби (а не к приближенному значению действительного числа!) благодаря точно определенным отношениям этих двух единиц.

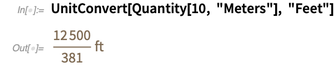
Физики (особенно) любят использовать «естественные» единицы. Часто эти натуральные единицы являются просто физическими константами или их комбинациями. Например, скорость света (здесь используется ввод на естественном языке).

Выраженная в единицах СИ (поскольку это скорость и требуются единицы измерения в метрах и секундах), скорость света имеет точное значение.

С другой стороны, постоянная Планка в настоящее время не имеет точного значения. Таким образом, его величина, выраженная в базовых единицах СИ, является приблизительным десятичным числом.

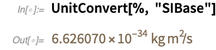
Обратите внимание, что точность 6.626070… отражает количество известных цифр.

Это последнее рекомендованное значение для постоянной Планка, опубликованное в CODATA 2017 для подготовки к уточнению констант. Ниже представлена соответствующая таблица:

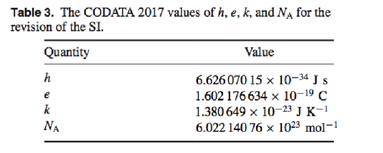
Физические константы (или их комбинации), которые связывают две физические величины, часто могут использоваться как натуральные единицы. Простейшими примерами будут измерение скорости в терминах скорости света или микроскопического вращательного момента в терминах ℏ. Или энергия может быть измерена в терминах массы с подразумеваемым фактором 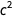. Функция DimensionalCombinations может быть использована для поиска комбинаций физических констант, которые позволяют связать две заданные физические величины. Например, могут быть построены следующие отношения между массой и энергией:

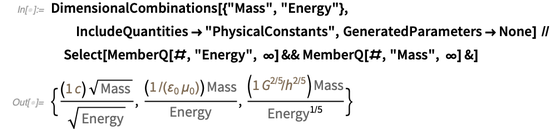
Первое равенство отражает знаменитую формулу Эйнштейна 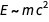, второе — это эквивалент первого соотношения, а третье — (размерностно) утверждает, что .

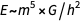2) Класс сущности «PhysicalConstant», недавно добавленный в Базу знаний Wolfram Knowledgebase.

Функции и объекты в языке Wolfram Language «рождаются вычислительно», то есть они готовы для использования и в вычислениях. Но для описания и моделирования реального мира нужны данные о реальном мире. Структура сущностей — это удобный и полностью интегрированный способ получения таких данных. Ниже представлены некоторые данные об электроне, протоне и нейтроне.

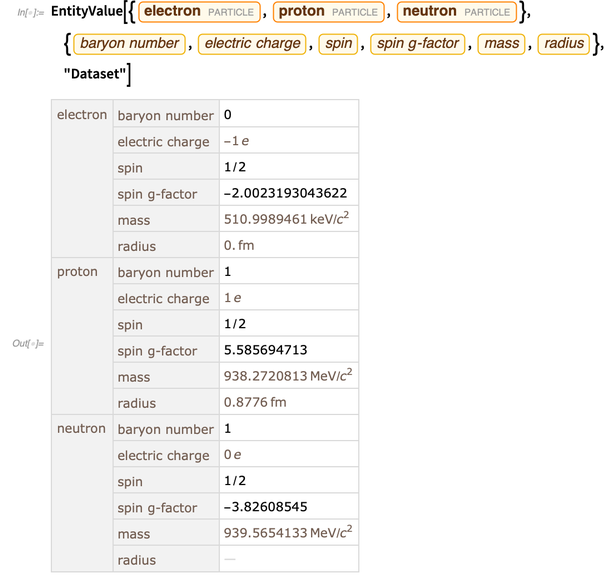
Одна из новых единиц сущности — это физические константы. В настоящее время База знаний содержит более 250 физических констант.

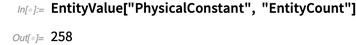
Ниже представлена дюжина случайно выбранных примеров. Причем без четкого определения того, что именно представляют собой физические постоянные, массы фундаментальных частиц, параметры Лагранжа стандартной модели и т. д. Для удобства список также содержит астрономические постоянные в соответствии с Астрономическим альманахом.

Большинство фундаментальных физических констант были названы константами класса C в известной работе Жана-Марка Леви-Леблона Ниже приведены константы классов C и B.

Возьмем, например, естественную единицу времени, время Планка. Функции ToEntity и FromEntity позволяют легко переходить туда и обратно между физическими константами как единицами и физическими константами как сущностями. Ниже демонстрируется сущность, соответствующая единице планковского времени.

База знаний имеет множество метаинформации о нем, например, его значения в последних списках CODATA.

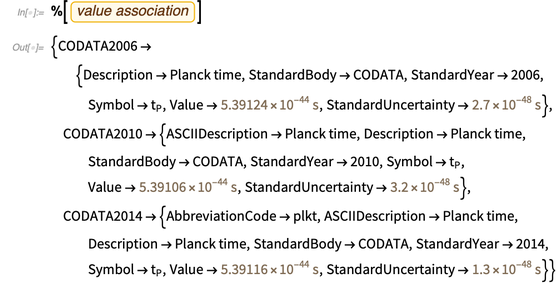
Последний вывод, который содержит значение и погрешность, подводит нас к третьей важной функции, которая будет полезна позже:

3) Введение функции Around [] в версии 12 языка Wolfram Language. Функция Around [] предоставляет неточное значение, указывая среднее значение и погрешность. Арифметическая модель Around [] базируется на GUM (Руководство по выражению погрешности в измерениях) — не путать с Plus-Minus-calculus Лейбница. Вот такое значение с погрешностью.

Наиболее важным и полезным аспектом вычислений со значениями, которые имеют погрешности, является то, что они должным образом учитывают корреляции. Наивное использование таких значений в арифметических числах или интервалах может недооценивать или переоценивать возникающую погрешность.

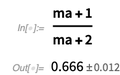
Ниже видим, что функция AroundReplace[] учитывает корреляцию.

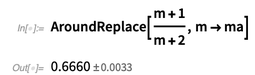
Вернемся к письму редактору

Теперь давайте используем эти три компонента и более подробно упомянутое письмо Уильяма Гофа редактору.

При текущих приблизительных значениях для e и ℏ, эти два значения для постоянной тонкой структуры согласуются в пределах их погрешностей. Первое — это выражение из письма к редактору, а второе — количество (Quantity[]), представляющее константу тонкой структуры.

Каждые несколько лет CODATA публикует официальные значения фундаментальных констант (см. константы тонкой структуры); как я уже говорил, значения, используемые в языке Wolfram Language, являются последними значениями CODATA и конечная погрешность отражается в точности числа.

Обратите внимание, что непосредственно измеренное значение постоянной тонкой структуры немного точнее, чем то, которое выражает постоянную тонкой структуры через другие константы.

Если мы используем предстоящие точные значения e и ℏ, и используем текущее точное значение 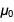, мы получим следующее точное значение для постоянной тонкой структуры в форме .

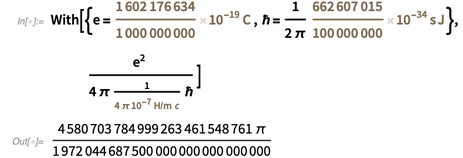
Маловероятно, что Господь, который даже не играет в кости, выбрал бы такое число для значения 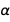в нашей вселенной. Это означает, что пока e и ℏ будут зафиксированы в новой СИ, текущие точные значения 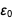и 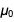неизбежно должны быть “расфиксированы” (см. также статью Голдфарба о величине 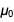новой СИ). (Мы вернемся к тому, почему 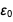и 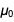вскоре должны стать неточными.)

Это означает, что после 20 мая этого года эти результаты станут другими, отличающимися от приведенных ниже.

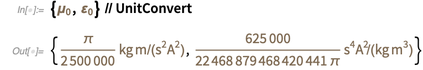
(В кратком примечании, класс сущности "PhysicalConstant" также имеет предполагаемые значения для констант, таких как константа тонкой структуры):

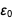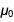Теперь, если не считать теологического аргумента о точной форме постоянной тонкой структуры, с физической точки зрения, почему и должны быть неточными? В качестве аргумента вероятности давайте рассмотрим 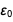. Один из самых выдающихся результатов, это закон Кулона.

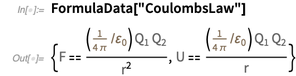
В существующей системе СИ ампер имеет «точное» определение:

Ампер является тем постоянным током, который, если его поддерживать в двух параллельных проводниках бесконечной длины с незначительным круглым поперечным сечением и размещенных на расстоянии 1 метра в вакууме, будет создавать между этими проводниками силу, равную ньютона на метр длины.

Это определение использует чисто механические величины ньютон и метр (то есть, после расширения, это секунда, метр и килограмм). Никакой взаимосвязи с зарядом электрона не делается, и в существующей системе СИ элементарный заряд является экспериментально измеренной величиной.

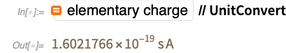
И это экспериментально измеренное значение изменилось за эти годы став более точным.

Сила в левой части закона Кулона (выраженная в ньютонах) содержит базовую единицу килограмм, который после того, как значение постоянной Планка становится постоянным, также становится точно определимым. Поскольку нет оснований предполагать, что все законы природы могут быть выражены в конечных рациональных числах, единственно возможной «движущейся частью» в законе Кулона будет 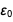. Его числовое значение должно быть определено, и оно сделает так, чтобы левая и правая сторона закона Кулона совпадала.

С более фундаментальной точки зрения физики, константа тонкой структуры является постоянной взаимодействия, которая определяет силу электромагнитных взаимодействий. И, возможно, однажды физика сможет вычислить значение постоянной тонкой структуры, но мы еще далеки от этого. Просто выбор определений единиц не может зафиксировать значение .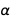

Действительно ли оба 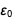и 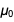становятся нефиксированными, или возможно сохранить один из них точным? Из-за уже точной скорости света и соотношения , если одно из 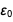или 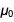точное, другое также должно быть точным. Мы знаем, что по крайней мере одно должно стать незафиксированным, поэтому из этого следует, что оба должны быть незафиксированными.

Значения, которые теперь даны постоянной Планка, постоянной Больцмана, постоянной Авогадро и элементарному заряду, не являются ни произвольными, ни полностью определенными. Они определяются примерно до восьми знаков, так что единицы измерения, которые они определяют после 20 мая, соответствуют «размеру» единиц, которые они определяют до 20 мая. Но цифры справа внизу не определены. Таким образом, значение будущей точной величины элементарного заряда может бы быть 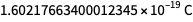, а не . Это бритва Оккама и рациональность, которые позволяют нам использовать .

На более техническом уровне подмена в предыдущем вычислении заключалась в том, что через термин в формуле 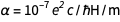использовался ампер до переопределения (помните 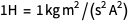), но также было использовано и точное значение элементарного заряда, означающее определение ампера после переопределения. И нам всегда нужно оставаться в одной системе единиц.

Вычисление таблицы форм, оптимизированных по погрешности

Итак, возникает естественный вопрос: какими должны быть эти «нефиксированные» значения? В моем последнем блоге я «вручную» создал новое значение 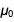. То, что можно сделать вручную, можно сделать с помощью компьютерной программы, поэтому давайте реализуем небольшую программу, которая вычисляет оптимизированную по погрешности форму производных физических констант. В ориентированном на будущее подходе, класс-сущность из семи констант, который определяет новую SI, уже доступен.

Ниже представлены константы, которые будут иметь точное значение в новой СИ.

Текущие значения этих постоянных вместе с их погрешностью (вычисляемые с помощью функции Around[]) имеют вид:

Используя класс сущности «PhysicalConstant» мы можем получить новые, предстоящие значения физических величин. Обратите внимание, что, как и во всех компьютерных языках, точные целые и рациональные числа являются либо явными целыми числами, либо рациональными (но не десятичными) числами.

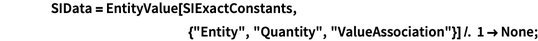
Многие физические константы могут быть связаны уравнениями, заданными физическими теориями различных областей физики. В дальнейшем мы хотим ограничиться теорией фундаментальных электромагнитных явлений, в которой погрешность констант будет сведена к погрешности постоянной тонкой структуры 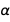и постоянной Ридберга 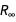. Если бы мы включили, например, гравитационные явления, мы должны были бы использовать гравитационную постоянную G, которая измеряется независимо, хотя она имеет очень большую погрешность (именно поэтому NSF имела так называемый «Big-G Challenge»).

Далее мы ограничимся электрическими, магнитными и массовыми величинами, погрешности которых сводятся к единицам 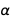и .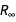

Ниже мы используем новую функцию Around для выражения значений с соответствующими погрешностям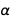и и .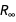

В настоящее время, в соответствии с CODATA 2014 относительная погрешность для 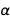составляет около 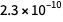, а для 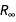около 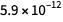. Как видим, погрешность для 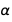больше чем для .

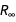Ниже приведен график log-базы-10 относительной погрешности 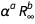как функции a и b. Очевидно, что для малых степеней относительная погрешность произведения слабо зависит от показателей степени a и b. Этот график показывает, что зависимость погрешности 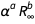доминирует относительно a (показатель степени тонкой структуры). Это наблюдение объясняется тем, что погрешность постоянной Ридберга в 50 раз меньше, чем погрешность постоянной тонкой структуры.

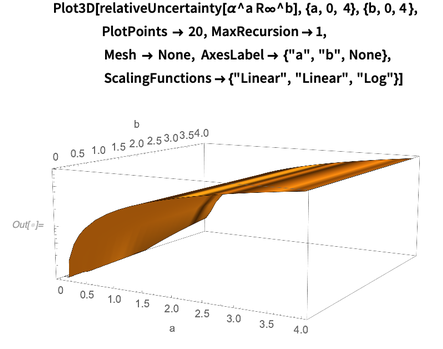
Чтобы вычислять погрешности различных констант в новой СИ, мы будем использовать следующие шаги:

• Извлечение эквивалентных представлений для физических констант, доступных из класса сущностей «PhysicalConstant».

Эти тождественные равенства между физическими константами являются законами физики и как таковые должны сохраняться как в старой, так и в новой СИ.

• Воспринимать формулы как набор алгебраических равенств, к которым можно применять различные методы исключения, чтобы выразить константу через комбинацию семи базовых постоянных новой СИ, а также константы тонкой структуры 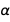и константы Ридберга .

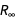Это те девять основных постоянных, которые мы разрешаем применять в определениях каждой новой рассматриваемой константы. (Технически в списке 10 констант, но из-за простого соотношения масштабирования между h и ℏ, в этом списке реально находятся девять «разных» констант.)

Класс сущности объекта “PhysicalConstant” содержит много информации об отношениях между физическими постоянными. Например, здесь приведены эквивалентные формы четырех констант, которые в настоящее время измеряются и скоро будут определены как имеющие точные значения.

В пределах точности измеренных значений все эти единичные элементы работают и сейчас. Вот быстрая численная проверка альтернативных форм постоянной Планка. Но конкретное числовое значение, особенно погрешность, зависит от фактической формы представления. Используя Around[], мы можем легко вычислить результирующие погрешности.

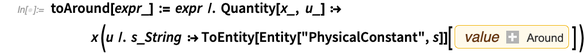
Ниже приведено графическое изображение результирующих погрешностей различных представлений. Очень большая погрешность десятков представлений может быть прослежена до большой погрешности во второй постоянной излучения.

И опять же в рамках погрешности констант, эти отношения должны сохраниться после переопределения. Так какое же из этих представлений лучше всего использовать после переопределения, чтобы минимизировать погрешности? Возможно, ни один из приведенных эквивалентов не является оптимальным, и, комбинируя некоторые из этих представлений, возможно удастся построить лучший, который имеет меньшую результирующую погрешность.

Теперь для последующих шагов алгебраических исключений, мы конвертируем константы, встречающиеся в эквивалентных классах (это возможно, потому что вторые аргументы в Entity ["PhysicalConstant",.] и в Quantity [1 ,.] приравнены). Причина, по которой мы используем сущности, а не величины в последующих вычислениях, двояка: во-первых, сущности являются удобными, легко читаемыми представлениями; и во-вторых, алгебраические функции (такие как GroebnerBasis) не проникают внутрь величин, чтобы определить природу их первого аргумента.

Затем мы делаем все тождества полиномами. Последний шаг означает: (1) вычитание левой стороны из правой стороны; и (2) что никакие дробные степени (например, квадратные корни) констант больше не появляются. Такое преобразование в полином мы осуществляем отыскивая все дробные показатели и находя LCM (наименьший общий множитель) всех их знаменателей.

Ниже приведено одно из предыдущих уравнений, которое содержит константы с дробной степенью.

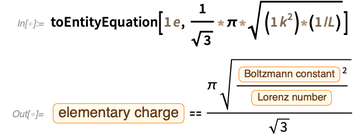
После полиномиализации мы приходим к многочленам нескольких переменных в трех присутствующих константах. Эти многочлены должны быть устранены.

Следующая таблица демонстрирует как функция toPolynomial, применяется к эквивалентным формам, показанным ранее для элементарного заряда. После канонизации ℏ в 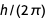, некоторые из полученных многочленов становятся идентичными.

Теперь, на основе имеющихся физических констант (без констант, используемых при определении новой SI), мы получаем достаточное количество эквивалентных форм для создания набора уравнений.

Ниже приведен список полученных полиномиальных уравнений для выражения элементарного заряда.

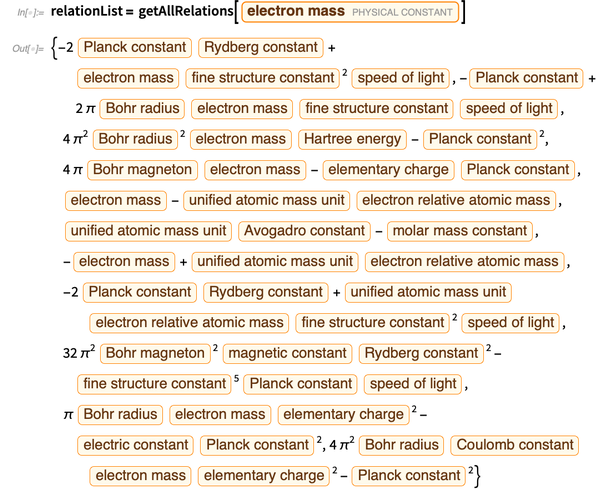
Выразим все погрешности через погрешност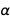и и . Только этих двух констант достаточно, чтобы выразить погрешность многих физических констант. И поскольку их погрешности не зависят друг от друга, и поскольку погрешности довольно малы, то эти две довольно известные постоянные лучше всего подходят для выражения оптимизированной (в смысле погрешностей) новой версии многих физических констант. И, конечно, мы допускаем все семь точных констант из новой СИ; поскольку они являются точными величинами, их наличие не изменит погрешности.

Основная работа по выражению заданной константы через константы СИ 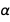и и 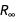будет осуществляться функцией GroebnerBasis. Настройка параметра MonomialOrder -> ElventionOrder является критически важным шагом, который удаляет все «не нужные» физические величины, оставляя одно полиномиальное уравнение с точно определенными константами и (при необходимости) тонкой структурой и константами Ридберга.

Путем исключения постоянных, связанных массой электрона, получим .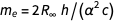

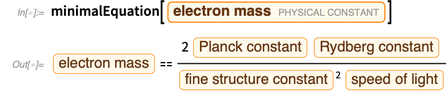
Погрешность этого выражения возникает от члена 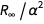. Мы можем определить функцию, которая удаляет член 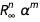, вызывающий погрешность.

Для более компактного представления, мы можем определить функцию, которая возвращает эквивалентную форму, а также старые и новые погрешности — в форме строки.

Мы заканчиваем блог представлением таблицы старых и новых погрешностей для более десятка физических констант. Этот список выбран в качестве репрезентативного примера; другие константы могут обрабатываться аналогичным образом (это может потребовать добавления дополнительных неточных констант для сохранения, таких как гравитационная постоянная или параметры стандартной модели).

Объединение строк в таблицу дает следующий результат для оптимального представления этих постоянных в новой системе единиц SI.

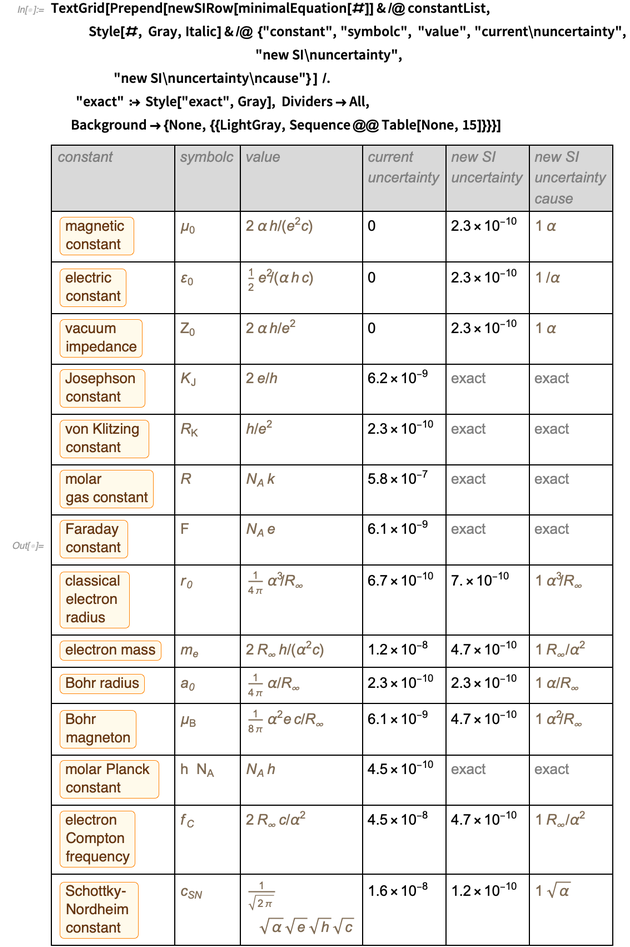
Это была таблица, которую мы намеревались вывести, и нам удалось ее вывести. Обратите внимание на появление 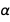в числителе и знаменателе 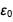и таким образом, что после сокращения результат 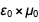становится 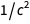. Подобный список можно найти в нижней части страницы Википедии о переопределении единиц СИ.