R в C++

Последнее время, по теме R на хабре появляются все новые посты: habrahabr.ru/post/161625/#habracut, habrahabr.ru/post/162583/. И мне захотелось обратить внимание на один важный момент. R – это не только язык программирования, но и огромная математическая библиотека, с уклоном в статистическую обработку данных. В данной статье я хотел бы рассказать, как использовать R в программах, написанных на с++.

В своем составе R имеет сишный интерфейс, однако в нем представлено далеко не все. Чтобы использовать возможности R на полную, существуют специальные пакеты: Rcpp и RInside. Пример, рассматриваемый в данном посте писался под Ubintu 12.10, хотя, насколько мне известно все необходимое есть и для Windows.

Установка необходимых пакетов

• Устанавливаем R и Rcpp: apt-get install r-base r-cran-rcpp2. Rcpp – библиотека для интеграции R в C++.
• 2. Запускаем R (в командной строке набираем: R) и устанавливаем дополнительные пакеты, из командной строки:
  1. RInside – это враппер над Rcpp, который делает работу с Rcpp очень простой
     install.packages(«RInside „), если не получилось скачиваем архив с cran.r-project.org/web/packages/RInside/index.html, затем опять в командной строке R: install.packages(file.choose(), repos=NULL), выбираем архив.
  2. Fitdistrplus – пакет расширяющий набор математических функции R
     install.packages(“fitdistrplus „), если не получилось скачиваем архив с cran.r-project.org/web/packages/fitdistrplus/index.html, затем опять в командной строке R: install.packages(file.choose(), repos=NULL), выбираем архив.

Теперь задача

Например, необходимо определить гипотезу распределения случайной величины.

Сначала рассмотрим как это выглядит в R:

library(fitdistrplus)    #Загрузим пакет, который легко позволяет определять основные моменты распределения.
x = rnorm(1000, 10, 5)    #Запишем в x 1000 значений с нормальным распределением, математическое ожидание – 10, ср. кв.           отклонение - 5
plot(x) #Посмотрим график

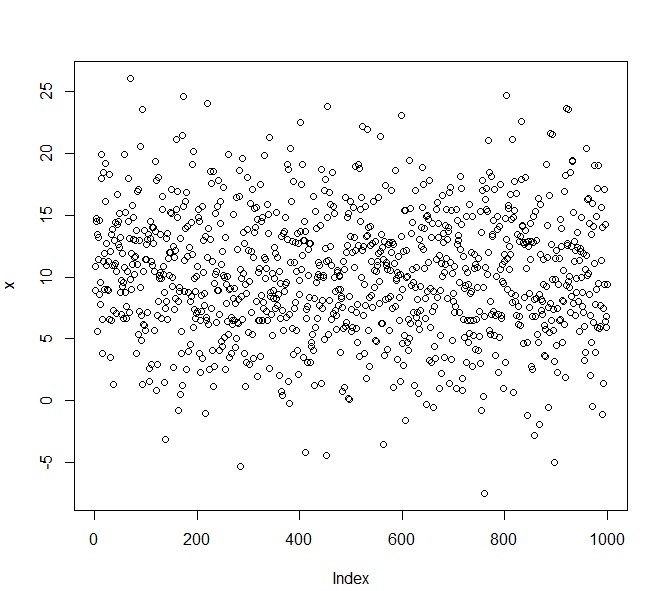
Для определения гипотезы распределения необходимо знать параметры распределения случайной величины. Найдем параметры (для нормального распределения: мат ожидание и ср. кв. отклонение) и запишем в переменные mean и sd.

params = fitdist(x, "norm");
mean = params[[1]][[1]]
sd = params[[1]][[2]] 

Теперь проверим гипотезу распределения на нормальный закон. Для этого будем использовать тест Колмогорова – Смирнова. При уровне значимости, альфа = 0.05 гипотеза должна быть отвергнута если альфа > p-value.

ks.test(x, "pnorm", mean, sd) 
#out:
#One-sample Kolmogorov-Smirnov test
#data:  x 
#D = 0.0199, p-value = 0.8236

p-value = 0.8236 > alfa -> гипотеза устраивает
Теперь проведем тот же тест, но в качестве исходных данных подсунем случайную величину распределенную по равномерному закону.

y = runif(1000, 0, 20)
plot(y)

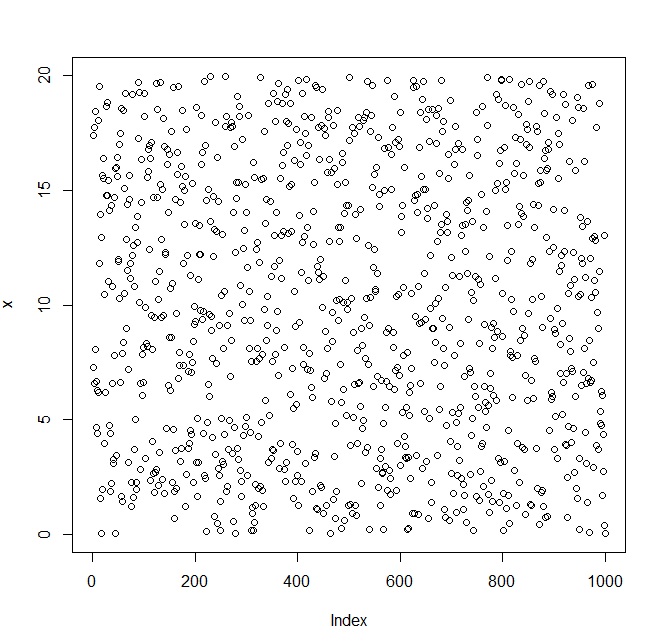
params = fitdist(y, "norm");
mean = params[[1]][[1]]
sd = params[[1]][[2]] 
ks.test(y, "pnorm", mean, sd)
#out
#One-sample Kolmogorov-Smirnov test
#data: y 
#D = 0.0659, p-value = 0.0003399

как видно p-value получился меньше alfa, следовательно гипотезу можно отвергнуть

Теперь попробуем повторить примерно тоже из c++.

Перед сборкой необходимо настроить пути на три пакета:
R, Rcpp, RInside (туда куда поставили):
Например R/include; Rcpp/include; RInside/include
R/lib; Rcpp/lib; RInside/lib

В этом примере мы создадим массив случайных чисел от 0 до 1000 и попробуем проверить гипотезу, что случайная величина распределена по нормальному закону.

Основная суть работы с R в C++ заключается в том, что мы заполняем строки на языке R и при помощи классов RInside и Rcpp выполняем их.

#include <RInside.h> 

int main(int argc, char *argv[]) {
    std::string evalstr = "";  // строка для формирования кода на R
    RInside R(argc, argv);  //окружение
    Rcpp::NumericVector RndVec(1000);  // создаем массив чисел
    for(int i = 0; i < 1000; ++i)
        RndVec(i) = (float)(rand() % 100); // заполняем его
    R["RndVec"] = RndVec; // связываем с массивом в R
    SEXP ans; // результат
    // формируем строку для R:
    // пробуем получить параметры распределения, считая, что это нормальный закон
    evalstr = "library(fitdistrplus) n 
    out <- fitdist(RndVec, "norm", 'mme')[[1]][[1]]; print(out); out";
    // получили результат
    ans = R.parseEval(evalstr);
    // получили матожидание 
    Rcpp::NumericVector mean(ans);
    std::cout << "mean " << " is " << mean[0] << std::endl;
    evalstr = "out <- fitdist(RndVec, "norm", 'mme')[[1]][[2]]; print(out); out";
    ans = R.parseEval(evalstr);
    // получили ско
    Rcpp::NumericVector sd(ans);
    std::cout << "sd " << " is " << sd[0] << std::endl;
    R["curMean"] = mean[0];
    R["curSd"] = sd[0];
    // выполнили тест
    evalstr = "out <- ks.test(RndVec, "pnorm", curMean, curSd)[[2]]; print(out); out";
    ans = R.parseEval(evalstr);
    Rcpp::NumericVector v1(ans);
    // посчитали p.value
    std::cout << "p.value " << " is " << v1[0] << std::endl;
    return 0;
}

Результат выполнения программы:

p.value is 0.000394703

Т.е. мы выбрали не верную гипотезу.

Заключение

Наверное код в данной статье не идеален, но цель была рассказать о возможности довольно просто использовать весь функционал R на c++, кроме того существуют библиотеки для подключения R к другим языкам, например java.

Ссылки

Вся информация доступна на вики en.wikipedia.org/wiki/R_(programming_language) + две статьи с хабра.

Автор: BoberCoder

Источник