По работе мне периодически приходится визуализировать численные данные — в виде таблиц, диаграмм или графиков. Из последнего прочитанного по теме наиболее интересной показалась известная книга Тафти The Visual Display of Quantitative Information. Я решил сделать из неё краткие выписки по относящимся к моим задачам вопросам. Ключевое слово здесь — краткие. Максимум полезной информации на минимум текста (даже стиль изложения будет подчёркнуто лапидарным). Дополнительные сведения и собственные мысли буду скрывать под спойлер. Надеюсь, мой конспект будет полезен хабрасообществу; предлагаю также поделиться своими наработками и полезными ссылками.
Чего следует избегать
1. Рисунков, объёмных изображений, массивных элементов диаграмм, несущих исключительно украшательскую функцию.
Примеры:



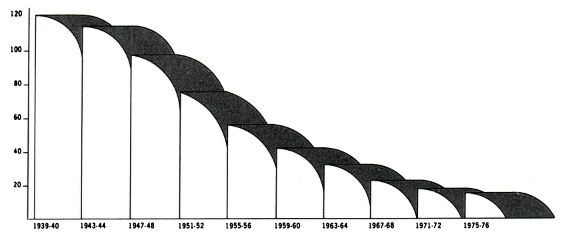
Причины: Трудно соблюсти правильные пропорции между числами и соответствующими рисунками (ср. фигуры врачей и бочек с числовыми данными). Даже если пропорции соблюдены, психологические исследования показывают, что люди плохо оперируют соотношениями площадей и объёмов изображённых фигур.
Примечание. Здесь и далее мы не обсуждаем сценарий преднамеренного желания автора исказить картину.
2. Представлений данных вне контекста.
Пример. Ниже приведён один и тот же факт (снижение смертности в 1956 году по сравнению с 1955 годом) (а) сам по себе; (б) в контексте более длинного промежутка времени); (в) также в сравнении с показателями соседних территорий:
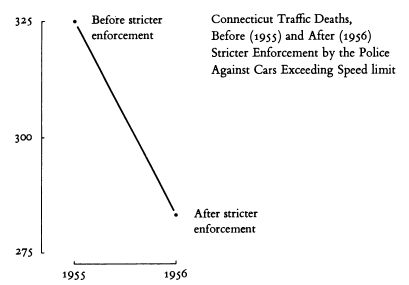
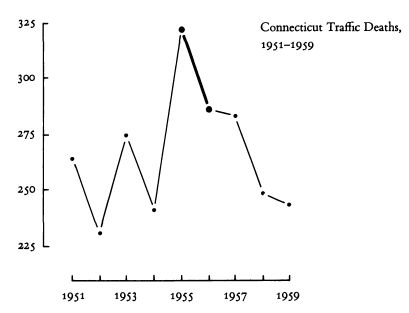
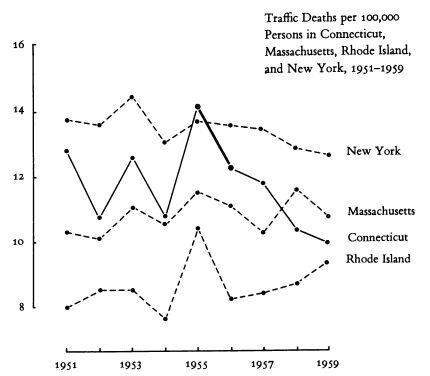
Причины: Визуализация — это инструмент анализа данных. Без соответствующего контекста анализ невозможен.
3. Штриховок.
Примеры:
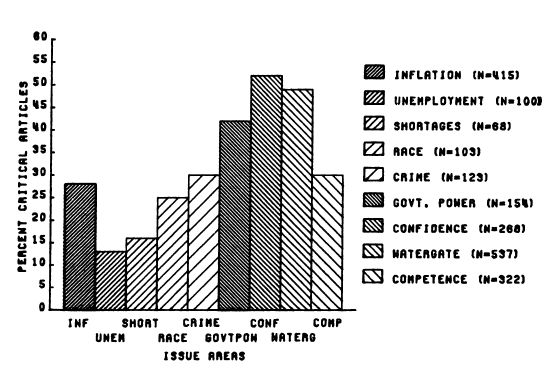
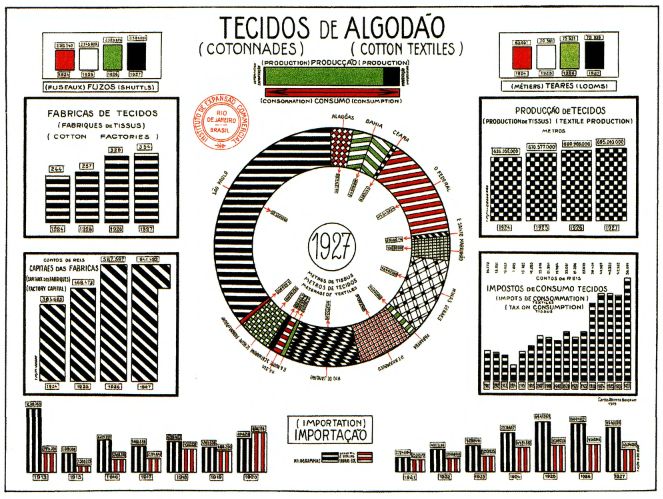
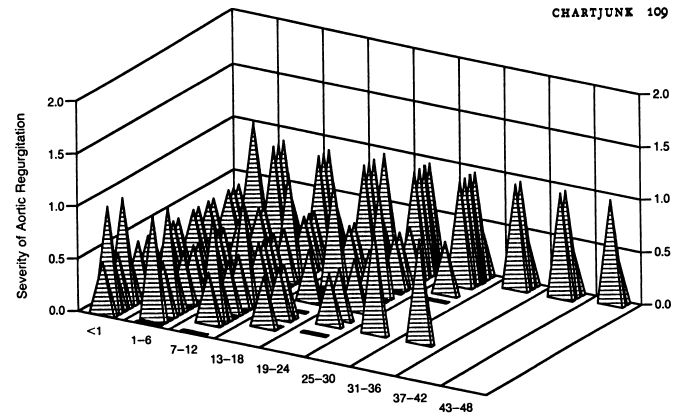
Причины: Эффект муара, рябь в глазах, затрудняющая анализ.
Примечание. Проблему предлагается решать не с помощью цветов (даже если это возможно технически), а упрощением самой графики.
4. Украшательств ради украшательств, цветов ради цветов (вырожденный случай пункта 1)
Пример:
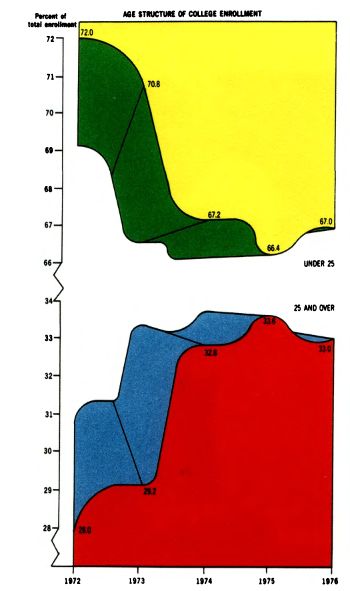
Причины: очевидны.
Примечание. Таблица — тоже инструмент визуализации. Не все данные нужно представлять графически. (Также аргументируется, что авторы склонны излишне упрощать графику: скажем, приведённая выше гистограмма с бочками может иллюстрировать сложный экономический текст, требующий известного образовательного уровня для восприятия. Сложность графики должна соответствовать сложности остального текста).
5. Цветового кодирования.
Пример:
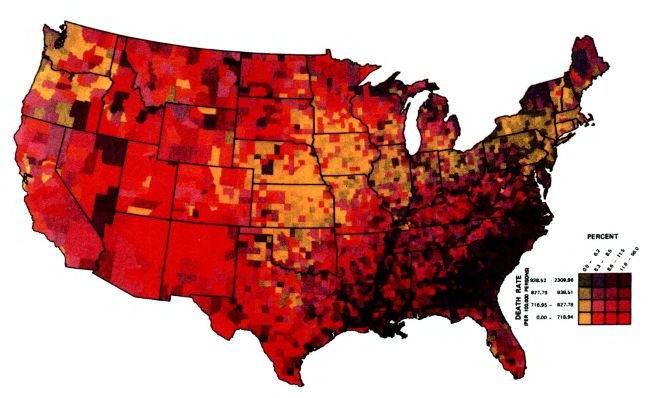
Причины: Цветовая шкала плохо воспринимается. Читатель вынужден постоянно возвращаться к «легенде». Утверждается, что даже цветовые переходы в виде радуги плохо интерпретируются. Единственный легко улавливаемый индикатор — насыщенность (т.е., например, оттенки серого допустимы).
6. Круговых диаграмм.
Пример:
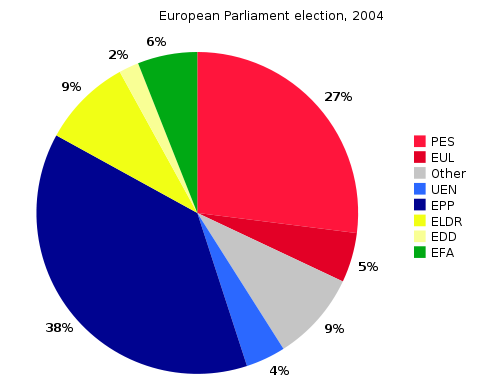
Причины: Доказано, что люди плохо воспринимают количественные соотношения между секторами круга. Если данные сложны, анализ с помощью круговой диаграммы невозможен. Если данные просты, лучше привести их в таблице.
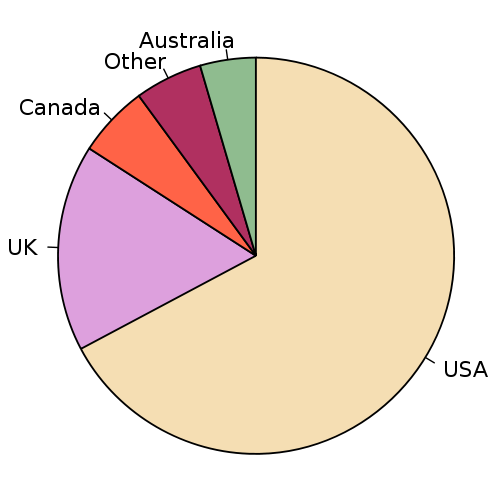
А многоуровневый пирог для анализа содержимого диска — вообще прекрасный элемент интерфейса:
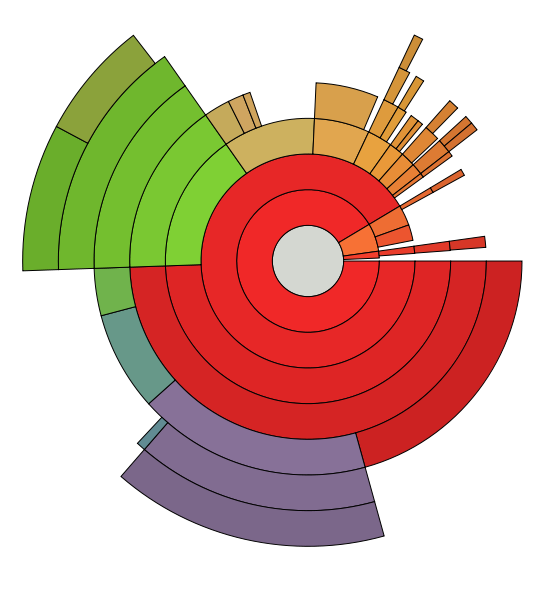
Методы улучшения визуализаций
1. Вынесение численной информации в графику.
Если численная информация (географическое расположение, транспортный поток, точка на объекте) может быть отображена на рисунке, имеет смысл сделать это.
Примеры:
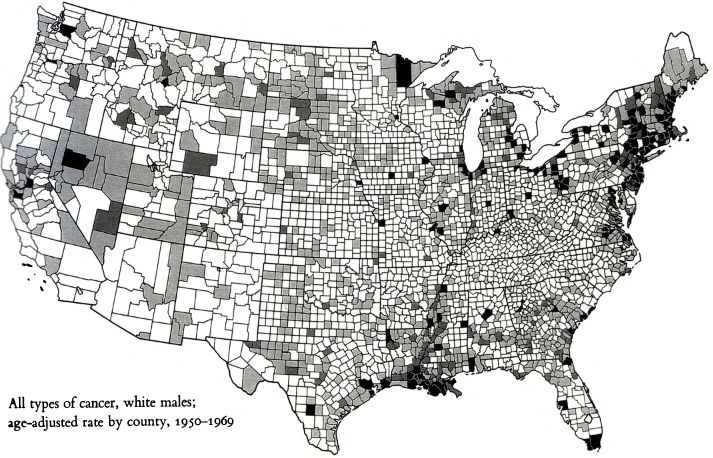
(Заболеваемость раком по регионам США)
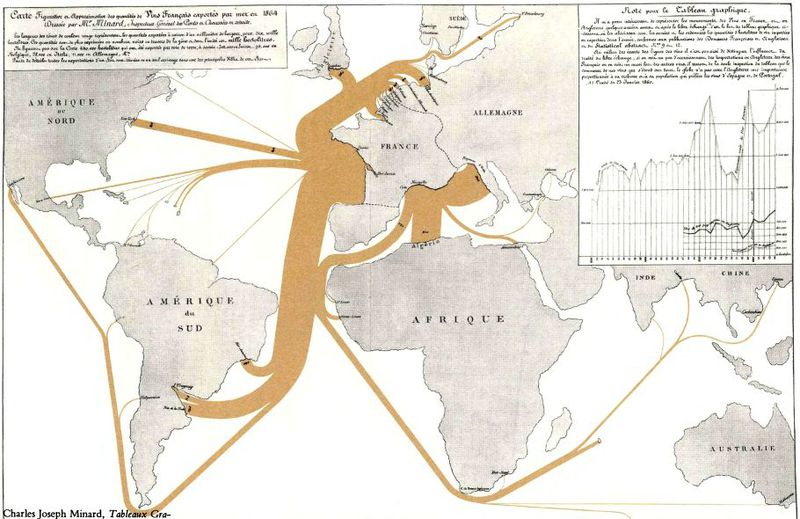
(Экспорт вина из Франции в различные страны мира)
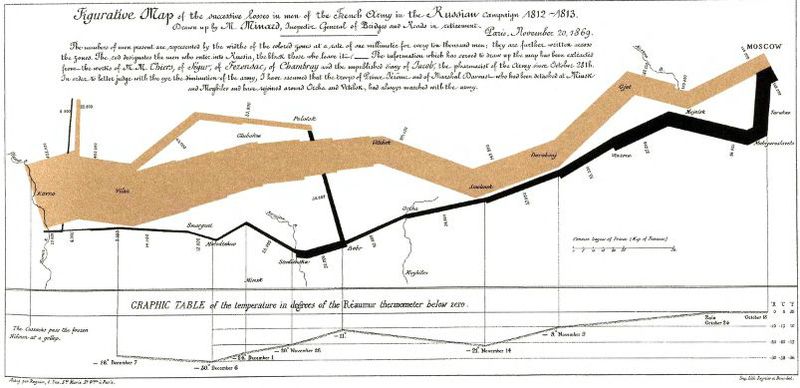
(Передвижения и численность армии Наполеона во время Русской кампании)
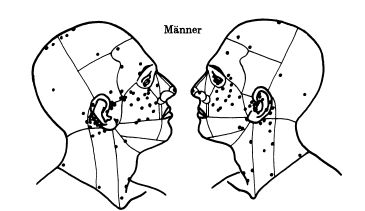
(Наиболее частые очаги возникновения меланомы на лице человека)
2. Увеличение data-to-ink ratio.
От элементов, не несущих смысловой нагрузки, следует избавляться, тем самым облегчая рисунок.
Примеры:
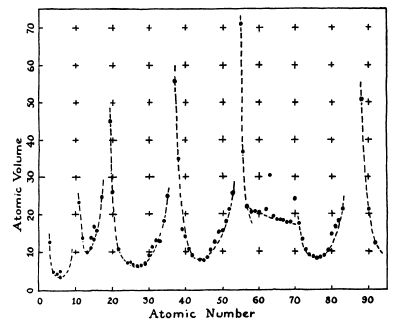

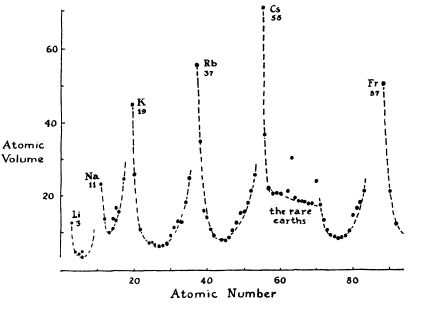
(Цель: показ периодической зависимости атомного объёма от атомного числа. На переработанном рисунке исключены элементы, не соответствующие цели, также добавлены пояснения для атомов «на краях» и для атомов, не вписывающихся в общую картину.)
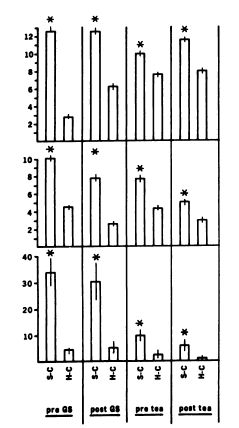

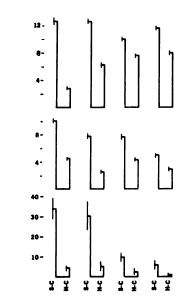
(Цель: показ того, что в каждом наборе из двух столбцов левый столбец всегда оказывается выше; длина вертикального штриха, пересекающего столбец, также имеет значение. В переработанном варианте сохраняются только значащие элементы.)
3. Редизайн существующих стандартных элементов диаграмм (специальный случай пункта 2).
Во-первых, не всегда новое решение мне кажется читабельнее старого. Та же «колбаса» выглядит именно как соединение двух элементов, хотя на самом деле визуализируются два независимых элемента.
Во-вторых, минимизируя избыточную графику, Тафти уж очень полагается на качество полиграфии. Массивные блоки заменяются точками и штрихами. Кое-где читателю предлагается оценивать значение по концу штриха, не оформленному никаким визуальным «якорем» (жирной точкой, перпендикулярной линией). Очень спорно, на мой взгляд.
В-третьих, существующие решения — это паттерны. Скажем, одну и ту же таблицу последовательности чисел можно отобразить как в виде гистограммы, так и в виде графика. Семантика этих решений, однако, различна. График отображает непрерывное изменение какого-либо параметра одного. Гистограмма применяется для дискретных значений, а также для отображения величин разных параметров (в этом случае каждый столбец соответствует своему параметру). Таким образом, к графическим решениям Тафти надо привыкать заново. Он считает, что это не проблема, поскольку все старые решения тоже когда-то были новыми.
В-четвёртых, использование новых элементов затруднительно, поскольку они слабо поддерживаются. Если выполнять чертёж от руки, нет разницы, что отображать. Если же пользоваться инструментами вроде Excel, приходится выбирать из имеющихся в наличии видов диаграмм. Ну или дорабатывать рисунок в графическом редакторе.
Примеры:
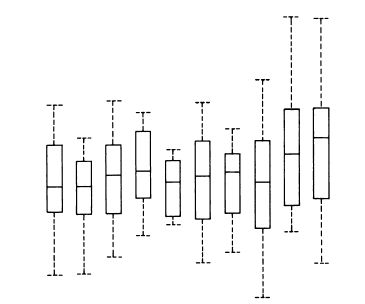
(«Диаграмма Тьюки») Пунктирная линия отображает некоторый диапазон. Границы прямоугольника обозначают первую и третью квартили диапазона, горизонтальная линия внутри прямоугольника — медиану диапазона.

Обычная гистограмма. Удалена «коробка»; штрихи, ранее обозначенные на оси ординат, выделены с помощью самих столбцов. (Тафти, однако, признаёт горизонтальную линию основы в качестве возможного визуального «якоря»).
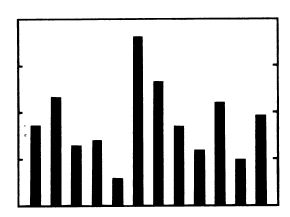

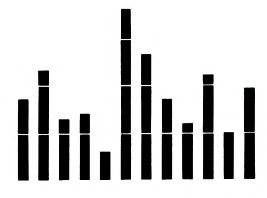
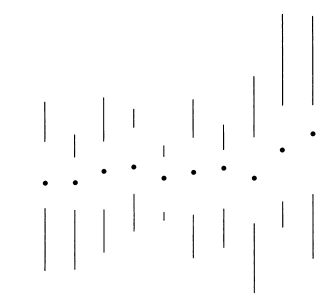
Диаграмма Тьюки с переменной шириной прямоугольника.
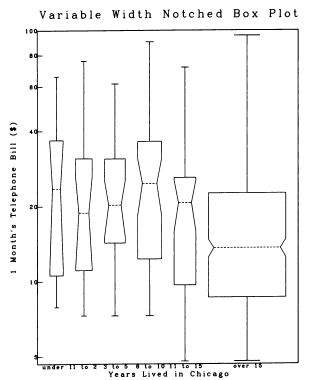

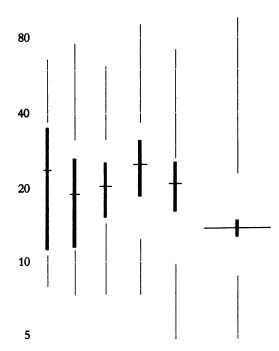
Обычный график с выделенными границами диапазона. Линия оси ординат покрывает лишь фактически присутствующую на графике часть диапазона (тем самым визуализируя минимум и максимум значений).
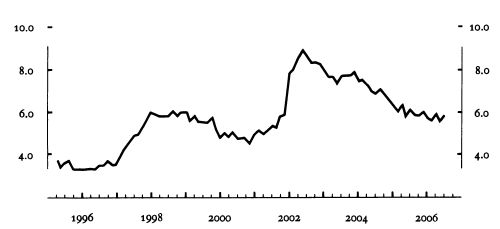
Диаграмма разброса (scatterplot). На обеих осях с помощью смещённой линии выделены квартили и медиана. Вместо смещённой линии можно использовать утолщение. Также оси покрывают лишь участок диаграммы от минимума до максимума.



Dot-dash-plot: вариант диаграммы разброса с возможностью анализа распределения величин по каждой из осей.
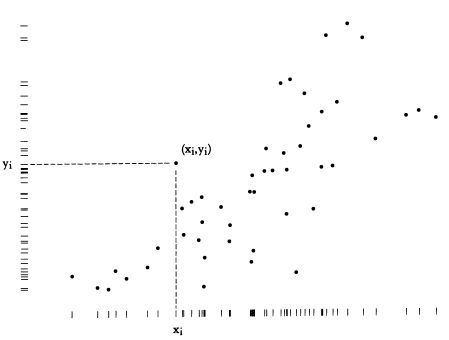
4. Использование данных в качестве элементов оформления
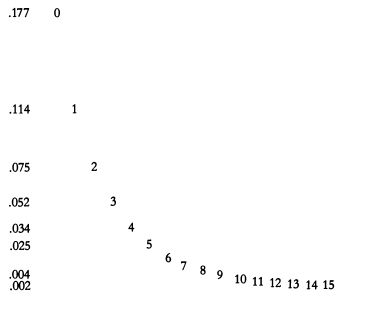
График, в котором подписи данных заменяют оси абсцисс и ординат. Отображены лишь реально встретившиеся в графике величины.
Жизненный цикл японского жука:

Мимика животного в зависимости от ситуации:

Заключение
В целом идеи Тафти сводятся к достаточно простым рекомендациям:
- не заниматься визуализацией тривиальных данных;
- избавляться от элементов, несущих только декоративную функцию;
- избавляться от элементов, затрудняющих анализ данных;
- максимизировать data-to-ink ratio;
- по возможности превращать элементы оформления (оси, точки) в элементы данных;
- по возможности использовать элементы данных в качестве элементов оформления;
- в рисунках по возможности отображать численные данные в графическом виде.
Автор: rg_software


