Введение
Прочитав недавно статью про список на Haskell, решил тоже немного рассказать о реализации базовых структур на ФЯП (F#). Статья не несёт практической ценности, поскольку готовых реализаций полно в интернете. Цель статьи — рассказать о том, как можно реализовать неизменяемую очередь на F# и как она работает.
Для начала немного терминологии.
F# — это язык программирования из семейства .NET, который, помимо объектно-ориентированного и императивного подходов, реализует функциональный подход в программировании.
Неизменяемые объекты – это такие объекты, которые будучи созданными один раз, в дальнейшем не могут быть изменены. Например, в C# есть такой тип данных, как string, экземпляры которого являются неизменяемыми. Добавляя символ в строку, вы получаете новую строку и имеете неизменной старую. Подробнее тут.
Односвязный список
Для реализации очереди нам понадобится односвязный список. Напомню, что односвязный список — это такая структура данных, каждый элемент которой содержит хранимое значение и ссылку на предыдущий элемент.
То же самое на F#:
type public 'a List = //Объявление типа List с generic-параметром 'a, указывающим тип хранимых значений
| Empty //Пустой список
| Node of 'a * 'a List //Пара: значение - остальной список ("хвост")
Эта запись означает, что список может быть либо пустым, либо представлять из себя пару «голова»-«хвост», где «хвост» тоже список.
Рассмотрим основные операции над списком и оценим их сложность.
Добавление элемента в список
Чтобы добавить элемент и при этом оставить неизменным старый список, нужно создать новый список, где голова – добавляемый элемент, хвост – старый список. На F# записывается одной строкой:
member this.Cons x = Node(x, this)
После этого мы имеем уже два списка: исходный и новый. При этом памяти оба списка занимают столько же, сколько бы занимал один конечный список (см. Рисунок ниже).
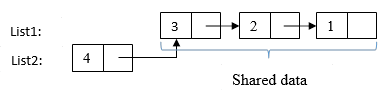
На рисунке List1 – список до добавления элемента, List2 – список после добавления элемента. При этом List1 также является «хвостом» списка List2.
Очевидно, что сложность добавления элемента не зависит от длины списка и равна O(1).
Извлечение элемента из списка
Извлечь элемент так же просто, как и добавить. Последний добавленный элемент просто берём из «головы»; для получения списка без этого элемента, берём «хвост».
member this.Head =
match this with
| Empty -> failwith "Empty stack"
| Node(head, tail) -> head
member this.Tail =
match this with
| Empty -> failwith "Empty stack"
| Node(head, tail) -> tail
Очевидно, что сложность и этих операций — О(1).
Разворот списка
Ещё одна полезная операция над списком – разворот, т.е. изменение порядка следования элементов. Для разворота необходимо последовательно извлекать элементы из оригинального списка и помещать их в новый. Новый и старый списки не будут иметь общих данных. Сложность будет всегда O(N). Код и иллюстрация ниже:
let rec reverse destList sourceList =
match sourceList with
| Empty -> destList
| Node(sourceHead, sourceTail) ->
reverse (Node(sourceHead, destList)) sourceTail
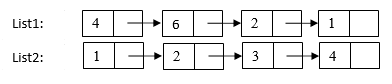
На рисунке List1 – список до разворота, List2 – после.
Очередь
Односвязный список с операциями добавления и извлечения элементов идеально подходит для реализации стека. Однако, если взять пару таких списков, можно реализовать очередь.
Очередь — структура данных с принципом доступа к элементам «первый пришёл — первый вышел» (FIFO).
Для реализации очереди понадобятся тыловой (rear) список, в который добавляются новые элементы, и фронтальный (front) список, из которого элементы извлекаются.
type 'a Queue (front:'a List, rear: 'a List) = // Объявление типа Queue как пары списков
static member Empty = Queue(List.Empty, List.Empty) // Пустая очередь - пара пустых списков
Добавление элемента в очередь
Добавление элемента в очередь — это есть добавление элемента в тыловой список, а точнее — это создание новой очереди, где фронтальный список тот же самый, а тыловой список получен добавлением нового элемента:
member this.Snoc value = Queue(front, rear.Cons value)
Очевидно, что оценка сложности добавления элемента в очередь совпадает с оценкой сложности добавления элемента в односвязный список – O(1).
Извлечение элемента из очереди
Перед тем, как извлечь элемент из фронтального списка, проверяем не пуст ли он. Если он пуст, берём тыловой и разворачиваем его – теперь он фронтальный, а тыловым назначаем пустой список. Сложность извлечения в худшем случае равна сложности разворота списка O(N).
let frontToBack =
match front, rear with
|Empty, rear -> (rear.Reverse, Empty)
|x -> (x)
member this.Head =
match frontToBack with
| Empty, _ -> failwith "Empty or not reversed"
| List.Node(a, __), _ -> a
member this.Tail =
match frontToBack with
|Empty, _ -> failwith "Empty"
|List.Node(a, tail), r -> Queue(tail, r)
Ниже приведена иллюстрация «из жизни» очередей, где отображено последовательное выполнение операций добавления и извлечения.
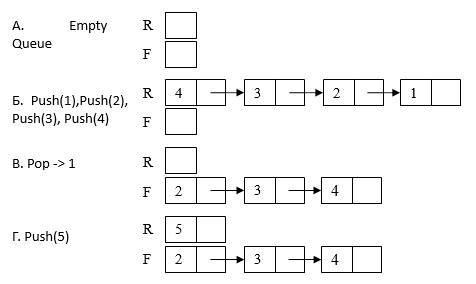
На рисунке схематично изображены четыре очереди: А – пустая очередь, Б – очередь после последовательного добавления чисел 1, 2, 3 и 4, В – очередь после извлечения одного элемента (числа 1), Г – очередь после добавления числа 5.
Заключение
Рассмотренный в начале статьи односвязный список может быть использован не только как стек, но и как коллекция с произвольным доступом. Для этого понадобятся операции вставки и удаления. Сложность их зависит от места вставки/удаления и в худшем случае равна O(N). Реализацию оставляю за читателем.
И список, и очередь для некоторых операций имеют не самую лучшую сложность — O(N). Ситуация может быть улучшена вплоть до O(1), если в реализации правильно применить ленивые вычисления. Как это делается, я расскажу в следующей статье, если уважаемый Читатель проявит к теме интерес.
Используемая литература
В качестве основного источника информации использовалась книга Chris Okasaki “Purely Functional Data Structures”
Автор: petuhov_k





