Расшифровка трассировщика лучей размером с открытку

«Он снова это сделал!», — вот, что первое пришло мне в голову, когда я посмотрел на оборотную сторону флаера Pixar ^[1], полностью заполненную кодом. Скопление конструкций и выражений была подписана в правом нижнем углу не кем иным, как Эндрю Кенслером. Для тех, кто его не знает, скажу: Эндрю — это программист, придумавший в 2009 году 1337-байтный трассировщик лучей размером с визитку.

На этот раз Эндрю придумал нечто более объёмное, но с гораздо более интересным визуальным результатом. Так как я закончил писать свои Game Engine Black Books про Wolf3D и DOOM, у меня появилось время на изучение внутренностей его загадочного кода. И почти сразу меня буквально очаровали обнаруженные в нём техники. Они сильно отличались от предыдущей работы Эндрю, основанной на «стандартном» трассировщике лучей. Мне было интересно узнать о ray marching, функциях конструктивной объемной геометрии, рендеринге Монте-Карло/трассировкой пути, а также множестве других трюков, которые он использовал, чтобы ужать код в такой небольшой кусок бумаги.

Исходный код

#include <stdlib.h> // card > pixar.ppm
#include <stdio.h>
#include <math.h>
#define R return
#define O operator
typedef float F;typedef int I;struct V{F x,y,z;V(F v=0){x=y=z=v;}V(F a,F b,F
c=0){x=a;y=b;z=c;}V O+(V r){R V(x+r.x,y+r.y,z+r.z);}V O*(V r){R V(x*r.x,y*r.
y,z*r.z);}F O%(V r){R x*r.x+y*r.y+z*r.z;}V O!(){R*this*(1/sqrtf(*this%*this)
);}};F L(F l,F r){R l<r?l:r;}F U(){R(F)rand()/RAND_MAX;}F B(V p,V l,V h){l=p
+l*-1;h=h+p*-1;R-L(L(L(l.x,h.x),L(l.y,h.y)),L(l.z,h.z));}F S(V p,I&m){F d=1
e9;V f=p;f.z=0;char l[]="5O5_5W9W5_9_COC_AOEOA_E_IOQ_I_QOUOY_Y_]OWW[WaOa_aW
eWa_e_cWiO";for(I i=0;i<60;i+=4){V b=V(l[i]-79,l[i+1]-79)*.5,e=V(l[i+2]-79,l
[i+3]-79)*.5+b*-1,o=f+(b+e*L(-L((b+f*-1)%e/(e%e),0),1))*-1;d=L(d,o%o);}d=sq
rtf(d);V a[]={V(-11,6),V(11,6)};for(I i=2;i--;){V o=f+a[i]*-1;d=L(d,o.x>0?f
absf(sqrtf(o%o)-2):(o.y+=o.y>0?-2:2,sqrtf(o%o)));}d=powf(powf(d,8)+powf(p.z,
8),.125)-.5;m=1;F r=L(-L(B(p,V(-30,-.5,-30),V(30,18,30)),B(p,V(-25,17,-25),V
(25,20,25))),B(V(fmodf(fabsf(p.x),8),p.y,p.z),V(1.5,18.5,-25),V(6.5,20,25)))
;if(r<d)d=r,m=2;F s=19.9-p.y;if(s<d)d=s,m=3;R d;}I M(V o,V d,V&h,V&n){I m,s=
0;F t=0,c;for(;t<100;t+=c)if((c=S(h=o+d*t,m))<.01||++s>99)R n=!V(S(h+V(.01,0
),s)-c,S(h+V(0,.01),s)-c,S(h+V(0,0,.01),s)-c),m;R 0;}V T(V o,V d){V h,n,r,t=
1,l(!V(.6,.6,1));for(I b=3;b--;){I m=M(o,d,h,n);if(!m)break;if(m==1){d=d+n*(
n%d*-2);o=h+d*.1;t=t*.2;}if(m==2){F i=n%l,p=6.283185*U(),c=U(),s=sqrtf(1-c),
g=n.z<0?-1:1,u=-1/(g+n.z),v=n.x*n.y*u;d=V(v,g+n.y*n.y*u,-n.y)*(cosf(p)*s)+V(
1+g*n.x*n.x*u,g*v,-g*n.x)*(sinf(p)*s)+n*sqrtf(c);o=h+d*.1;t=t*.2;if(i>0&&M(h
+n*.1,l,h,n)==3)r=r+t*V(500,400,100)*i;}if(m==3){r=r+t*V(50,80,100);break;}}
R r;}I main(){I w=960,h=540,s=16;V e(-22,5,25),g=!(V(-3,4,0)+e*-1),l=!V(g.z,
0,-g.x)*(1./w),u(g.y*l.z-g.z*l.y,g.z*l.x-g.x*l.z,g.x*l.y-g.y*l.x);printf("P
6 %d %d 255 ",w,h);for(I y=h;y--;)for(I x=w;x--;){V c;for(I p=s;p--;)c=c+T(e
,!(g+l*(x-w/2+U())+u*(y-h/2+U())));c=c*(1./s)+14./241;V o=c+1;c=V(c.x/o.x,c.
y/o.y,c.z/o.z)*255;printf("%c%c%c",(I)c.x,(I)c.y,(I)c.z);}}// Andrew Kensler

Он вообще работает?

$ clang -o card2 -O3 raytracer.cpp
$ time ./card > pixar.ppm

real	2m58.524s
user	2m57.567s
sys	0m0.415s

Спустя две минуты и пятьдесят восемь секунд^[3] генерируется следующее изображение. Потрясающе, насколько мало кода для него требуется.

Из показанного выше изображения можно извлечь очень многое. Зернистость — очевидный признак «трассировщика пути». Этот тип рендерера отличается от трассировки лучей (raytracing) тем, что лучи не трассируются обратно к источникам освещения. В этом способе из источников испускаются тысячи лучей на пиксель и программа следит за ними, надеясь, что он найдут источник освещения. Это интересная техника, которая гораздо лучше, чем трассировка лучей, справляется с рендерингом ambient occlusion, мягких теней, каустики и radiosity.

Разобьём код на части

#include <stdlib.h> // card > pixar.ppm
#include <stdio.h>
#include <math.h>

#define R return
#define O operator
typedef float F;typedef int I;

struct V{F x,y,z;V(F v=0){x=y=z=v;}V(F a,F b,F
c=0){x=a;y=b;z=c;}V O+(V r){R V(x+r.x,y+r.y,z+r.z);}V O*(V r){R V(x*r.x,y*r.
y,z*r.z);}F O%(V r){R x*r.x+y*r.y+z*r.z;}V O!(){R*this*(1/sqrtf(*this%*this)
);}};

F L(F l,F r){R l<r?l:r;}F U(){R(F)rand()/RAND_MAX;}F B(V p,V l,V h){l=p
+l*-1;h=h+p*-1;R-L(L(L(l.x,h.x),L(l.y,h.y)),L(l.z,h.z));}

F S(V p,I&m){F d=1
e9;V f=p;f.z=0;char l[]="5O5_5W9W5_9_COC_AOEOA_E_IOQ_I_QOUOY_Y_]OWW[WaOa_aW
eWa_e_cWiO";for(I i=0;i<60;i+=4){V b=V(l[i]-79,l[i+1]-79)*.5,e=V(l[i+2]-79,l
[i+3]-79)*.5+b*-1,o=f+(b+e*L(-L((b+f*-1)%e/(e%e),0),1))*-1;d=L(d,o%o);}d=sq
rtf(d);V a[]={V(-11,6),V(11,6)};for(I i=2;i--;){V o=f+a[i]*-1;d=L(d,o.x>0?f
absf(sqrtf(o%o)-2):(o.y+=o.y>0?-2:2,sqrtf(o%o)));}d=powf(powf(d,8)+powf(p.z,
8),.125)-.5;m=1;F r=L(-L(B(p,V(-30,-.5,-30),V(30,18,30)),B(p,V(-25,17,-25),V
(25,20,25))),B(V(fmodf(fabsf(p.x),8),p.y,p.z),V(1.5,18.5,-25),V(6.5,20,25)))
;if(r<d)d=r,m=2;F s=19.9-p.y;if(s<d)d=s,m=3;R d;}

I M(V o,V d,V&h,V&n){I m,s=
0;F t=0,c;for(;t<100;t+=c)if((c=S(h=o+d*t,m))<.01||++s>99)R n=!V(S(h+V(.01,0
),s)-c,S(h+V(0,.01),s)-c,S(h+V(0,0,.01),s)-c),m;R 0;}

V T(V o,V d){V h,n,r,t=
1,l(!V(.6,.6,1));for(I b=3;b--;){I m=M(o,d,h,n);if(!m)break;if(m==1){d=d+n*(
n%d*-2);o=h+d*.1;t=t*.2;}if(m==2){F i=n%l,p=6.283185*U(),c=U(),s=sqrtf(1-c),
g=n.z<0?-1:1,u=-1/(g+n.z),v=n.x*n.y*u;d=V(v,g+n.y*n.y*u,-n.y)*(cosf(p)*s)+V(
1+g*n.x*n.x*u,g*v,-g*n.x)*(sinf(p)*s)+n*sqrtf(c);o=h+d*.1;t=t*.2;if(i>0&&M(h
+n*.1,l,h,n)==3)r=r+t*V(500,400,100)*i;}if(m==3){r=r+t*V(50,80,100);break;}}
R r;}

I main(){I w=960,h=540,s=16;V e(-22,5,25),g=!(V(-3,4,0)+e*-1),l=!V(g.z,
0,-g.x)*(1./w),u(g.y*l.z-g.z*l.y,g.z*l.x-g.x*l.z,g.x*l.y-g.y*l.x);printf("P
6 %d %d 255 ",w,h);for(I y=h;y--;)for(I x=w;x--;){V c;for(I p=s;p--;)c=c+T(e
,!(g+l*(x-w/2+U())+u*(y-h/2+U())));c=c*(1./s)+14./241;V o=c+1;c=V(c.x/o.x,c.
y/o.y,c.z/o.z)*255;printf("%c%c%c",(I)c.x,(I)c.y,(I)c.z);}}

// Andrew Kensler

Каждый из разделов подробно описан в оставшейся части статьи:
■ — обычные трюки, ■ — класс Vector, ■ — вспомогательный код, ■ — база данных, ■ — Ray marching, ■ — сэмплирование, ■ — основной код.

Обычные трюки с #define и typedef

Класс V

struct Vec {
    float x, y, z;

    Vec(float v = 0) { x = y = z = v; }
    Vec(float a, float b, float c = 0) { x = a; y = b; z = c;}

    Vec operator+(Vec r) { return Vec(x + r.x, y + r.y, z + r.z); }
    Vec operator*(Vec r) { return Vec(x * r.x, y * r.y, z * r.z); }
    // dot product
    float operator%(Vec r) { return x * r.x + y * r.y + z * r.z; }
    // inverse square root
    Vec operator!() {return *this * (1 / sqrtf(*this % *this) );}
};

Заметьте, что здесь отсутствует оператор вычитания (-), поэтому вместо записи «X = A — B» используется «X = A + B * -1». Обратный квадратный корень пригождается в дальнейшем для нормализации векторов.

Функция Main

int main() {
  int w = 960, h = 540, samplesCount = 16;
  Vec position(-22, 5, 25);
  Vec goal = !(Vec(-3, 4, 0) + position * -1);
  Vec left = !Vec(goal.z, 0, -goal.x) * (1. / w);

  // Cross-product to get the up vector
  Vec up(goal.y * left.z - goal.z * left.y,
         goal.z * left.x - goal.x * left.z,
         goal.x * left.y - goal.y * left.x);

  printf("P6 %d %d 255 ", w, h);
  for (int y = h; y--;)
    for (int x = w; x--;) {
      Vec color;
      for (int p = samplesCount; p--;)
        color = color + Trace(position, !(goal + left * (x - w / 2 + randomVal())+ 
        up * (y - h / 2 + randomVal())));

      // Reinhard tone mapping
      color = color * (1. / samplesCount) + 14. / 241;
      Vec o = color + 1;
      color = Vec(color.x / o.x, color.y / o.y, color.z / o.z) * 255;
      printf("%c%c%c", (int) color.x, (int) color.y, (int) color.z);
    }
}

Заметьте, что литералы типа float не содержат буквы «f», а дробная часть отбрасывается для экономии места. Тот же трюк используется ниже, где отбрасывается целочисленная часть (float x = .5). Также необычна конструкция «for» с выражением итерации, вставленное внутрь условия останова.

Это довольно стандартная функция main для трассировщика лучей/пути. Здесь задаются векторы камеры и для каждого пикселя испускаются лучи. Разница между трассировщиком лучей и трассировщиком пути в том, что в ТП на пиксель испускается несколько лучей, которые слегка сдвинуты случайным образом. Затем цвет, полученный для каждого луча в пикселе накапливается в трёх float-каналах R,B,G. В конце выполняется тональная коррекция результата метододм Рейнхарда.

Самая важная часть — это sampleCount, которому теоретически можно присвоить значение 1 для ускорения рендеринга и итераций. Вот примеры визуализаций со значениями сэмплов от 1 до 2048.

Заголовок спойлера

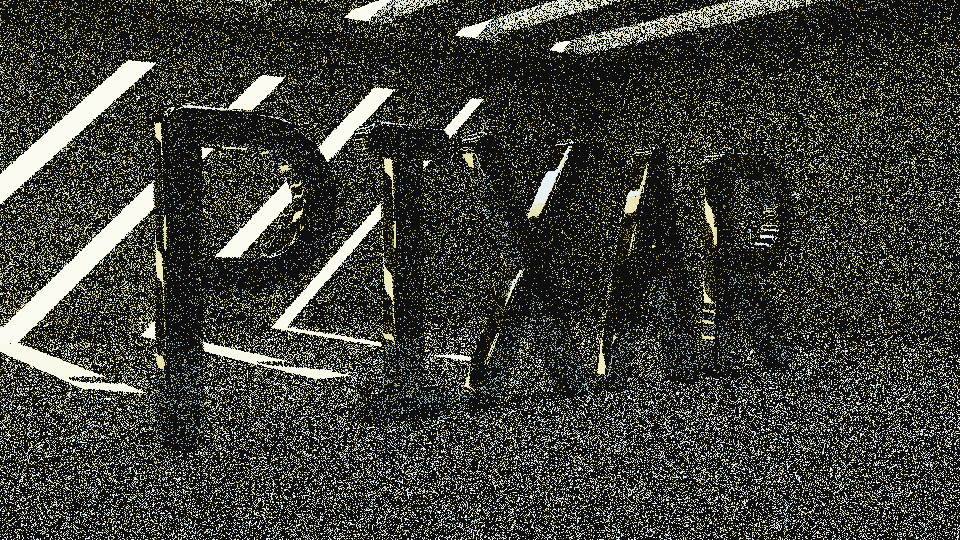
1

2

4

8

16

32

64

128

256

512

1024

2048

Вспомогательный код

float min(float l, float r) { return l < r ? l : r; }
float randomVal() { return (float) rand() / RAND_MAX; }

// Rectangle CSG equation. Returns minimum signed distance from 
// space carved by lowerLeft vertex and opposite rectangle
// vertex upperRight.
float BoxTest(Vec position, Vec lowerLeft, Vec upperRight) {
  lowerLeft = position + lowerLeft * -1;
  upperRight = upperRight + position * -1;
  return -min(
    min(
      min(lowerLeft.x, upperRight.x), 
      min(lowerLeft.y, upperRight.y)
    ), 
    min(lowerLeft.z, upperRight.z));
}

Функции конструктивной объёмной геометрии

// Signed distance point(p) to sphere(c,r)
  float testSphere(Vec p, Vec c, float r) {
    Vec delta = c - p;
    float distance = sqrtf(delta%delta);
    return radius - distance;
  }  

  Vec A {4, 6}; 
  Vec B {3, 2}; 
  Vec C {4, 2}; 
  float r = 2.;

  testSphere(A, C, r); // == -1 (outside)
  testSphere(B, C, r); // ==  1 (inside)

Функция testSphere() возвращает -1 для точки A (то есть она снаружи) и 1 для B (то есть она внутри). Знаки у расстояний — это просто трюк, позволяющий получить два элемента информации вместо одного в случае одного значения. Подобный тип функции можно написать и для описания параллелограмма (именно это и выполняется в функции function BoxTest).

  // Signed distance point(p) to Box(c1,c2)
  float testRectangle(Vec p, Vec c1, Vec c2) {
    c1 = p + c1 * -1;
    c2 = c2 + position * -1;
    return min(
      min(
        min(c1.x, c2.x), 
        min(c1.y, c2.y)), 
      min(c1.z, c2.z));
  }  

  Vec A  {3, 3}; Vec B  {4, 6};
  Vec C1 {2, 2}; Vec C2 {5, 4};
  testRectangle(A, C1, C2); //  1.41 (inside)
  testRectangle(B, C1, C2); // -2.23 (outside)

Теперь давайте посмотрим, что получится, если перевернуть знак возвращаемого значения.

  // Signed distance point(p) to carved box(c1,c2)
  float testCarveBox(Vec p, Vec c1, Vec c2) {
    c1 = p + c1 * -1;
    c2 = c2 + position * -1;
    return -min(
      min(
        min(c1.x, c2.x), 
        min(c1.y, c2.y)), 
      min(c1.z, c2.z));
  }  

  Vec A  {3, 3}; Vec B  {4, 6};
  Vec C1 {2, 2}; Vec C2 {5, 4};
  testCarveBox(A, C1, C2); // == -1.41 (outside)
  testCarveBox(B, C1, C2); // ==  2.23 (inside)

Теперь мы не описываем твёрдый объект, а объявили твёрдым весь мир и вырезаем в нём пустое пространство. Функции можно использовать как строительные кирпичики, которые при комбинировании могу сочетании описывают более сложные формы. С помощью оператора логического сложения (функция min) мы можем вырезать пару прямоугольников один над другим и результат будет выглядеть следующим образом.

  // Signed distance point to room    
  float testRoom(Vec p) {
    Vec C1 {2, 4}; Vec C2 {5, 2}; // Lower room
    Vec C3 {3, 5}; Vec C4 {4, 4}; // Upper room

    // min() is the union of the two carved volumes.
    return min(testCarvedBox(p, C1, C2),
               testCarvedBox(p, C3, C4));
  }

  Vec A  {3, 3}; 
  Vec B  {4, 6};
  testRoom(A, C1, C2); // == -1.41 (outside)
  testRoom(B, C1, C2); // ==  1.00 (inside)

Если задуматься, то это выглядит как исследуемая нами комната, потому что именно так выражена нижняя комната — с помощью двух вырезанных параллелограммов.

Теперь, овладев могучими познаниями CSG, мы можем вернуться к коду и рассмотреть функцию базы данных, с которой разобраться сложнее всего.

#define HIT_NONE 0
#define HIT_LETTER 1
#define HIT_WALL 2
#define HIT_SUN 3

// Sample the world using Signed Distance Fields.
float QueryDatabase(Vec position, int &hitType) {
  float distance = 1e9;
  Vec f = position; // Flattened position (z=0)
  f.z = 0;
  char letters[15*4+1] =               // 15 two points lines
          "5O5_" "5W9W" "5_9_"         // P (without curve)
          "AOEO" "COC_" "A_E_"         // I
          "IOQ_" "I_QO"                // X
          "UOY_" "Y_]O" "WW[W"         // A
          "aOa_" "aWeW" "a_e_" "cWiO"; // R (without curve)

  for (int i = 0; i < sizeof(letters); i += 4) {
    Vec begin = Vec(letters[i] - 79, letters[i + 1] - 79) * .5;
    Vec e = Vec(letters[i + 2] - 79, letters[i + 3] - 79) * .5 + begin * -1;
    Vec o = f + (begin + e * min(-min((begin + f * -1) % e / (e % e),
                                      0),
                                 1)
                ) * -1;
    distance = min(distance, o % o); // compare squared distance.
  }
  distance = sqrtf(distance); // Get real distance, not square distance.

  // Two curves (for P and R in PixaR) with hard-coded locations.
  Vec curves[] = {Vec(-11, 6), Vec(11, 6)};
  for (int i = 2; i--;) {
    Vec o = f + curves[i] * -1;
    distance = min(distance,
                   o.x > 0 ? fabsf(sqrtf(o % o) - 2)
                           : (o.y += o.y > 0 ? -2 : 2, sqrtf(o % o))
               );
  }
  distance = powf(powf(distance, 8) + powf(position.z, 8), .125) - .5;
  hitType = HIT_LETTER;

  float roomDist ;
  roomDist = min(// min(A,B) = Union with Constructive solid geometry
               //-min carves an empty space
                -min(// Lower room
                     BoxTest(position, Vec(-30, -.5, -30), Vec(30, 18, 30)),
                     // Upper room
                     BoxTest(position, Vec(-25, 17, -25), Vec(25, 20, 25))
                ),
                BoxTest( // Ceiling "planks" spaced 8 units apart.
                  Vec(fmodf(fabsf(position.x), 8),
                      position.y,
                      position.z),
                  Vec(1.5, 18.5, -25),
                  Vec(6.5, 20, 25)
                )
  );
  if (roomDist < distance) distance = roomDist, hitType = HIT_WALL;

  float sun = 19.9 - position.y ; // Everything above 19.9 is light source.
  if (sun < distance)distance = sun, hitType = HIT_SUN;

  return distance;
}

Можно увидеть здесь функцию «вырезания» параллелограмма, в которой для построения целой комнаты используется всего два прямоугольника (всё остальное делает наш мозг, он представляет, что это стены). Горизонтальная лестница — это чуть более сложная CSG-функция, использующая деление с остатком. И, наконец, буквы слова PIXAR составлены из 15 линий с парой «начало координат/дельта» и двумя особыми случаями для кривых в буквах P и R.

Ray Marching

// Perform signed sphere marching
// Returns hitType 0, 1, 2, or 3 and update hit position/normal
int RayMarching(Vec origin, Vec direction, Vec &hitPos, Vec &hitNorm) {
  int hitType = HIT_NONE;
  int noHitCount = 0;
  float d; // distance from closest object in world.

  // Signed distance marching
  for (float total_d=0; total_d < 100; total_d += d)
    if ((d = QueryDatabase(hitPos = origin + direction * total_d, hitType)) < .01
            || ++noHitCount > 99)
      return hitNorm =
         !Vec(QueryDatabase(hitPos + Vec(.01, 0), noHitCount) - d,
              QueryDatabase(hitPos + Vec(0, .01), noHitCount) - d,
              QueryDatabase(hitPos + Vec(0, 0, .01), noHitCount) - d)
         , hitType; // Weird return statement where a variable is also updated.
  return 0;
}

Идея ray marching с учётом расстояний заключается в том, чтобы двигаться вперёд на расстояние до ближайшего объекта. В конце концов луч приблизится к поверхности настолько, что точку можно будет считать точкой падения.

Заметьте, что ray marching возвращает не истинное пересечение с поверхностью, а приближение. Именно поэтому в коде marching останавливается, когда d < 0.01f.

Собираем всё вместе: сэмплирование

Vec Trace(Vec origin, Vec direction) {
  Vec sampledPosition, normal, color, attenuation = 1;
  Vec lightDirection(!Vec(.6, .6, 1)); // Directional light

  for (int bounceCount = 3; bounceCount--;) {
    int hitType = RayMarching(origin, direction, sampledPosition, normal);
    if (hitType == HIT_NONE) break; // No hit. This is over, return color.
    if (hitType == HIT_LETTER) { // Specular bounce on a letter. No color acc.
      direction = direction + normal * ( normal % direction * -2);
      origin = sampledPosition + direction * 0.1;
      attenuation = attenuation * 0.2; // Attenuation via distance traveled.
    }
    if (hitType == HIT_WALL) { // Wall hit uses color yellow?
      float incidence = normal % lightDirection;
      float p = 6.283185 * randomVal();
      float c = randomVal();
      float s = sqrtf(1 - c);
      float g = normal.z < 0 ? -1 : 1;
      float u = -1 / (g + normal.z);
      float v = normal.x * normal.y * u;
      direction = Vec(v,
                      g + normal.y * normal.y * u,
                      -normal.y) * (cosf(p) * s)
                  +
                  Vec(1 + g * normal.x * normal.x * u,
                      g * v,
                      -g * normal.x) * (sinf(p) * s) + normal * sqrtf(c);
      origin = sampledPosition + direction * .1;
      attenuation = attenuation * 0.2;
      if (incidence > 0 &&
          RayMarching(sampledPosition + normal * .1,
                      lightDirection,
                      sampledPosition,
                      normal) == HIT_SUN)
        color = color + attenuation * Vec(500, 400, 100) * incidence;
    }
    if (hitType == HIT_SUN) { //
      color = color + attenuation * Vec(50, 80, 100); break; // Sun Color
    }
  }
  return color;
}

Я немного поэкспериментировал с этой функцией, чтобы изменить максимальное количество допустимых отражений луча. Значение «2» придаёт буквам на удивление красивую лакированную окраску Vantablack^[4].

1

2

3

4

Полностью очищенный исходный код

Справочные материалы

[2] Источник: Википедия: формат изображений NetPBM

[3] Источник: Визуализация выполнена на максимально мощном MacBook Pro, 2017

[4] Источник: Википедия: Vantablack

Автор: PatientZero

Источник