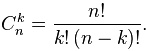В обсуждении проекта «большого глупого носителя» OTRAG, состоящего из пакета простых ракет, неоднократно поднимался вопрос надёжности такого количества двигателей. Вспоминалась печальная история советской сверхтяжёлой ракеты Н-1, у которой на первой ступени стояло 30 двигателей, и которая ни разу за четыре полёта не долетела до конца её работы. В комментарии рассказать про теорию вероятностей и расчёт надёжности места нет, поэтому предлагаю вашему вниманию занимательный рассказ о количестве двигателей, надёжности, комбинаторике и теории вероятностей.
Задача первая, ознакомительная

Для начала рассмотрим простой пример. Представим себе, что у нас есть ракета. Мы можем поставить на неё один мощный двигатель или четыре средних двигателя. У всех двигателей надёжность 0,9. То есть, если мы 100 раз запускали эти двигатели в полёт, они работали нормально в ~90 случаях. В каком случае у нашей ракеты будет выше надёжность — на мощном двигателе или на средних?
Полёт ракеты с одним мощным двигателем будет, очевидно, успешен с вероятностью 0,9.
Если для успешного полёта ракеты нужно, чтобы успешно отработали все 4 двигателя, то их надёжности надо перемножить. Т.е.
Pуспеха на средних двигателях=0,9*0,9*0,9*0,9=0,6561
Получается, что из 100 запусков ракета на одном мощном двигателе долетит в 90 случаях, а на четырёх средних — всего в 66 случаях. Казалось бы, OTRAG с 64 блоками для вывода 1 тонны на орбиту обречён. Однако, не всё так просто. А если мы возьмём четыре двигателя с такой же надёжностью, но такой тягой, что для успешного выведения на орбиту хватит трёх двигателей из четырёх? Как рассчитать надёжность в этом случае?
В этом случае вероятность успешного полёта будет рассчитываться следующим образом:
Во-первых, с вероятностью 0,94=0,6561 все четыре двигателя отработают нормально.
Событие «этот двигатель вышел из строя, а остальные отработали нормально» имеет вероятность 0,1*0,93. Поскольку всего двигателей 4, нужно умножить вероятность этого события на 4:
4*0,1*0,93=0,2916
События «все двигатели отработали нормально» и «один двигатель вышел из строя» не могут произойти одновременно и входят в полную группу возможных исходов, поэтому мы можем их сложить для подсчёта вероятности успешного исхода:
Pуспеха на средних двигателях с возможностью одного отказа=0,6561+0,2916=0,9477
Вот так вот, один избыточный двигатель сделал нашу ракету гораздо надёжней. Продолжим наши расчеты дальше. А что, если наши «средние» двигатели стали настолько мощными, что даже в случае двух отказов ракета успешно выйдет на орбиту?
Вероятность события «все двигатели отработали успешно» нам известна — 0,6561.
Вероятность события «отказал один двигатель» тоже известна — 0,2916.
Найдем вероятность события «отказали два двигателя». Вероятность события «отказали этот и этот двигатели, а остальные отработали нормально» равна 0,12*0,92. Но сколькими способами можно выбрать два двигателя из четырех?
Число сочетаний Cnk — читается как «C из n по k» — это количество способов, которым можно выбрать k элементов из множества n элементов, если элементы не возвращаются обратно после выбора и их порядок не имеет значения. Формула расчёта:
Нам нужно выбрать два двигателя из четырёх, поэтому C42=4!/(2!(4-2)!)=(1*2*3*4)/((1*2)*(1*2)=24/4=6.
Отсюда следует, что вероятность события «отказали два двигателя» равна 6*0,12*0,92=0,0486, и
Pуспеха на средних двигателях, допускающих до двух отказов=0,6561+0,2916+0,0486=0,9963
Если приглядеться, получается достаточно простая закономерность:
Pвсе двигатели отработали успешно=C40*0,10*0,94=0,6561
Pотказал один двигатель=C41*0,11*0,93=0,2916
Pотказали два двигателя=C42*0,12*0,92=0,0486
Pотказали три двигателя=C43*0,13*0,91=0,0036
Pотказали все четыре двигателя=C44*0,14*0,90=0,0001Как и положено для полной группы событий, сумма вероятностей дает 1.
Вывод: Зная надёжность компонентов, мы можем рассчитать, сколько резервных элементов обеспечат нам требуемую надёжность.
Надёжность OTRAG

Для начала, попробуем рассчитать, была ли заранее заложена ненадёжность блоков в виде резервных CRPU в ракете? Известно, что для вывода одной тонны на орбиту предлагалось использовать три ступени — из 48, 12 и 4 блоков. Взяв данные по массе и удельному импульсу, посчитаем запас характеристической скорости для полезной нагрузки в одну тонну по формуле Циолковского:
dVтретьей ступени=2910 м/с*ln((1 т ПН+4*1,5 т)/(1 т ПН + 4*0,15 т))=4,3 км/с
dVвторой ступени=2910 м/с*ln((7 т ПН и третьей ступени+12*1,5 т)/(7 т + 12*0,15 т))=3 км/с
dVпервой ступени=2646 м/с*ln((25 т ПН, второй и третьей ступеней+48*1,5 т)/(25 т + 48*0,15 т))=2,9 км/с
Сумма: 10,2 км/с
Характеристическая скорость в диапазоне 9,3-10 км/с обычна и означает, что запаса для резервирования скорее всего не было. Теперь попробуем рассчитать, сколько дополнительных блоков нам потребуется для получения высоконадёжной ракеты. Начальные условия:
- Известно, что надёжность OTRAG по испытаниям была 0,9355
- Необходимо спроектировать ракету с надежностью блоков не ниже 0,9
- Суммарный запас характеристической скорости должен быть не меньше, чем у исходной ракеты
- Отказом ступени будем считать незапуск/разрушение двигателя при включении с условно мгновенным стравливанием компонентов. Сценарий, в котором нужно тащить на орбиту отказавший блок весом 1,5 тонны с топливом слишком пессимистичный.
- Дополнительной сложностью будет необходимость стабилизации ракеты. Для простоты будем считать, что одновременно с отказавшим блоком выключается второй блок с противоположной стороны, а его компоненты условно мгновенно сливаются.
Третья ступень
С третьей ступенью самая большая сложность. Всего 4 блока не допускают возможности выключения хотя бы одного из них при сохранении сколько-нибудь адекватного запаса характеристической скорости.
Четыре блока надёжностью 0,9355 без резервирования имеют надёжность 0,93554=0,77. Мало. Добавим ещё два блока. Вероятность успеха шестиблоковой ступени с возможностью отказа одного блока составит 0,93556+6*0,0645*0,93555=0,9475. С точки зрения надёжности шести блоков достаточно.
Рассчитаем запас характеристической скорости новой ступени для случая отказа одного блока и выключения второго для симметрии тяги. Расчет в WolframAlpha дает 3,9 км/с. Попробуем добавить седьмой блок:
Запас характеристической скорости: 4,24 км/с
Надёжность семиблоковой ступени с возможностью отказа одного блока: 0,93.
В реальности отказ блока далеко не обязательно произойдёт на первой секунде полёта, поэтому я выберу оптимистичный вариант шестиблоковой третьей ступени.
Вторая ступень
Поскольку у нас четыре блока превратились в 6, необходимо пересчитать количество блоков на второй ступени, которые дали бы такой же запас характеристической скорости. Масса третьей ступени+ПН выросла с 7 то 10 тонн, методом подбора определяем, что нам необходимо не меньше 17 блоков для такого же запаса delta-V. Возьмем 18 блоков для симметрии конструкции.
Сколько блоков мы можем позволить себе потерять для случая 18-блоковой ступени?
Допустим один отказ, надежность: 0,67
Допустимы два отказа, надежность: 0,89
У большой системы из многих блоков есть интересная особенность. Отказы могут произойти на разных сторонах ступени и компенсировать тягу самостоятельно, без необходимости выключать дополнительные блоки. Разная глубина отказавших блоков может потребовать меньшего количества выключенных блоков для компенсации. Только если нам совсем не повезёт, отключатся два соседних блока на краю ступени, и нам потребуется выключать два противоположных блока. Расчёт надёжности в этом случае — это отдельный сложный процесс, я для простоты буду считать необходимое количество выключенных для компенсации блоков как половину допустимых отказавших. Проще говоря, ставим 20 блоков на вторую ступень. С отказом двух блоков и выключением одного блока на компенсацию нам примерно хватит запаса характеристической скорости.
Первая ступень
Вторая и третья ступень с ПН выросли с 25 т до 40. Следовательно, для того, чтобы разогнать их на 2,9 км/с нам потребуется целых 76 блоков.
В случае, когда у нас есть много независимых двигателей, мы можем посчитать наиболее вероятное количество отказов по формуле для биномиального распределения:
n*p-q<=k<=n*p+p, где
n — количество испытаний (в данном случае, блоков)
p — вероятность нужного исхода (в данном случае успеха)
q = 1 — pДля нашего случая второй ступени с 76 двигателями получим:
76*0,9355-0,0645<=k<=76*0,9355+0,9355
71<=k<=72
Следовательно, наиболее вероятен отказ 4-5 блоков.
Посчитаем надежность:
Допустим один отказ: 0,039
Допустимы до двух отказов: 0,12
Допустимы до трех отказов: 0,27
Допустимы до четырёх отказов: 0,45
Допустимы до пяти отказов: 0,63
Допустимы до шести отказов: 0,78
Допустимы до семи отказов: 0,88
Семь отказов, три блока на компенсацию (консервативный вариант). Методом подбора получаем, что нам потребуется ступень с 90 блоками.
Выводы
Третья ступень. Было 4 блока, стало 6.
Вторая ступень. Было 12 блоков, стало 20.
Первая ступень. Было 48 блоков, стало 90.
Всего было 64 блока, стало 116.
Обратите внимание, что при расчётах использовался очень консервативный подход. Во-первых, не учитывался тот факт, что отказ блока может произойти не при запуске, а спустя какое-то время работы, когда блок уже поучаствовал в разгоне ракеты. Во-вторых, использовалась реальная надёжность испытательных пусков. Простота и невысокие параметры нагрузки конструкции означают, что надёжность блока несложно повысить. В-третьих, цифровая система управления способна, используя терминальное наведение, компенсировать недобор характеристической скорости одной ступени запасом других ступеней.

Двигатель блока OTRAG. Простота поражает...
Что же касается печальной истории советской Н-1, её погубили не 30 двигателей, а тот факт, что первая ступень не тестировалась в сборе на стенде, а двигатели к ней не тестировались перед установкой. Конструкция двигателей НК-15 не позволяла многократный запуск. Партии двигателей тестировались выборочно (2 из 6), что не позволяло гарантированно не допустить бракованный двигатель на ракету. Отказ двигателя имел характер взрыва, что повреждало кабели, трубопроводы и соседние двигатели, делая дальнейший полёт невозможным.
Кстати, на ракетах-носителях семейства «Союз» на старте включаются пять двигателей с 32 камерами сгорания, и это не мешает «семёркам» быть очень надежными ракетами.
Автор: lozga