Независимо от размера и массы все дисковые галактики во Вселенной делают один полный оборот вокруг своей оси примерно за 1 миллиард лет. К такому выводу пришла группа астрофизиков из Международного центра радиоастрономических исследований (ICRAR) из Университета Западной Австралии. Как написано в пресс-релизе по результатам открытия, в этом смысле дисковые галактики можно сравнить с космическими часами.
В число дисковых галактик входят линзовидные и спиральные, как наш Млечный Путь или Галактика Андромеды неподалёку.
В соответствии с современной стандартной космологической моделью CDM (Cold Dark Matter), основные структурные и динамические свойства галактических гало (гало — сферический невидимый компонент галактики, состоящий в том числе из тёмной материи и содержащий основную массу галактики) и дисков (видимая часть) подчиняются простому вириальному масштабному соотношению. Эти свойства обычно определяются как радиус 
, скорость вращения 
и масса 
. Или, как вариант, яркость 
в качестве прокси для массы. Вириальный эквилибриум для гало соблюдается как 
к 
и к 
. Конечно, тёмная материя напрямую не наблюдается, однако масштабные соотношения наблюдаются через свойства барионов, хотя экспоненты в степенном законе этих соотношений не в точности соответствуют модели для гало.
Чаще всего на практике используется масштабное соотношение скорости и светимости, более известное как зависимость Талли — Фишера. Это эмпирически полученное соотношение, связывающее массу (светимость) спиральной галактики и скорость её вращения. Барионная физика очень сложна, она учитывает много факторов, которые могут повлиять и исказить все масштабные соотношения. Например, активное ядро галактики может перераспределить барионы, а в процессе затянуть в распределение барионов тёмную материю, из-за чего все вышеуказанные соотношения искажаются.
Хотя часто упоминается соотношение скорости вращения и светимости, но вот соотношению скорости вращения и радиуса до сих пор уделялось не так много внимания. Возможно, здесь ситуация усложняется трудностью в измерении радиуса по радиальной шкале.
В новой работе учёные применили для измерения масштабного соотношения для 
не радиальную шкалу, как в предыдущих работах, а внешний радиус галактики — и показали, что в этом случае наблюдается практически линейное соотношение 
.
Круговая скорость вращения соотносится с радиусом по всем наблюдаемым галактикам, которые отличаются по размерам и круговой скорости вращения в 30 раз: от карликовых неправильных галактик до гигантских спиральных.
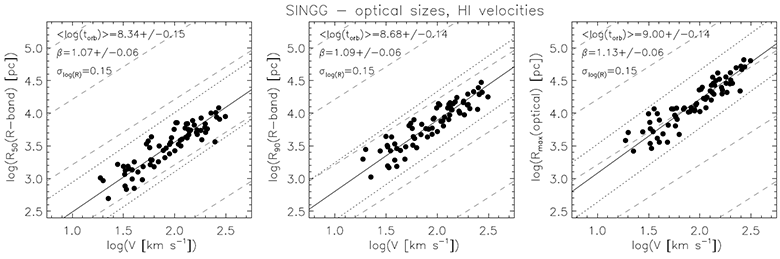
Соотношение радиуса и круговой скорости на логарифмической шкале
Другими словами, все дисковые галактики действительно работают как часы, совершая оборот примерно за 1 миллиард лет, если измерять по самому краю их дисков.
«Обнаружение такой закономерности в галактиках помогает лучше понять механику их вращения — вы не найдете быстро вращающуюся плотную галактику, в то время как другая галактика такого же размера, но меньшей плотности вращается медленнее», — говорит профессор Герхардт Мейрер (Gerhardt Meurer) из Университета Западной Австралии.
Правда, исследователи делают оговорку, что для подтверждения этого универсального закона следует провести измерения по более широкому набору дисковых галактик, чтобы полностью исключить предвзятость при отборе.
Кроме того, учёные обращают внимание, что на внешней границе галактического диска находятся не только плотные скопления молодых звёзд и межзвёздного газа, но и большое количество намного более старых звёзд, смешанных с молодыми и межзвёздным газом. У галактического диска довольно чёткая граница. Зная скорость вращения, можно вычислить радиус и быстрее обнаружить эту границу.
Авторы научной работы говорят, что после долгожданного вступления в строй радиотелескопа Square Kilometer Array (SKA) в их распоряжение поступит огромный массив данных о галактиках. Тогда точная наводка, где искать границы галактики, поможет при обработке этого большого количества информации.
Научная работа опубликована 9 марта 2018 года в журнале The Monthly Notices of the Royal Astronomical Society (doi: 10.1093/mnras/sty275, pdf).
Автор: Анатолий Ализар
