В этой статье я представлю вам результаты исследований, которые проводил я сам. Алгоритмы или алгоритмические композиции использовались в создании музыки многие столетия. Например, западный контрапункт иногда может быть сведен к алгоритмической избыточности. Почему бы не использовать быстро обучаемые компьютеры, производящие миллиарды вычислительных операций в секунду, по назначению – для выполнения алгоритмов? В этой статье я этим и займусь, используя машинное обучение и цепь Маркова второго порядка.
Граф представляет матрицу переходов цепи Маркова (будет объяснена позднее) с разученными 8 композициями
Цепь Маркова?
Цепь Маркова, названа в честь Маркова Андрея Андреевича, и представляет собой псевдослучайный процесс перехода из одного состояния в другое. Переход происходит без запоминания предыдущего состояния (такой переход называется «марковостью»), и зависит только от текущего состояния и вероятностей, которые представлены в так называемой матрице переходов. Короче говоря, переход из одного состояние в другое – это случайный процесс, носящий вероятностный характер.
Основная идея
Цепь Маркова идеально подходит для создания алгоритмических музыкальных композиций. Ноты (128 из них) – это вероятностные состояния. Для реализации всего процесса я буду использовать цепь Маркова второго порядка, а это означает, что следующее состояние системы будет строиться на основании двух предыдущих (нот). Все вероятности хранятся в матрице размерностью 2^14x2^7. На входе синтезатор получает два целых числа (0 <= n, m <= 127), выступающих в качестве начальных нот. На их основании алгоритм вычисляет/генерирует следующую ноту и продолжает процесс вычисления до бесконечности (до тех пор, пока вы его не остановите). Для упрощения задачи, громкость звучания всех нот будет одинаковой (127), как и временной интервал между ними (300 мс).
Вычисление вероятностей и весов для матрицы переходов цепи Маркова второго порядка
Для вычисления матрицы переходов цепи Маркова используется матрица весов. Как я уже говорил, в алгоритме используется цепь Маркова второго порядка, поэтому в процессе вычислений участвуют три ноты. Для каждой комбинации из трех нот первые две всегда являются «начальным» состоянием, а третья «конечным»; результатом всегда является инкрементация соответствующего поля в матрице весов [первая нота*127+вторая нота][третья нота].
Разумеется, это всего лишь начало всего процесса. После расстановки всех весов в соответствии с нотами, матрица весов «нормализуется» (или конвертируется) в матрицу переходов путем замены целых чисел на их процентное отношение к сумме всех значений в строке. Отрывки кода ниже реализуют оба описанных процесса. Две матрицы сведены в одну, названную scoreMatrix.
Генерация матрицы весов:
public static void updateWeight(int n1, int n2, int n3) {
scoreMatrix[n1*127+n2][n3]++;
}
Нормализация матрицы весов/генерация матрицы переходов:
public static int sumAll(int pos) {
int sum = 0;
for(int i = 0; i < 128; sum+=scoreMatrix[pos][i++]);
return sum;
}
public static void normalizeMatrix() {
for(int i = 0; i < 128*128; i++) {
int sum = sumAll(i);
if(sum != 0)
for(int j = 0; j < 128; j++)
scoreMatrix[i][j] /= sum;
}
}
Непосредственно процесс обучения
Процесс обучения возвращает матрицу весов, которая после его завершения конвертируется в матрицу переходов. Алгоритм, описываемый в этой статье, использует для обучения MIDI-файлы (с расширением .mid). Алгоритм обрабатывает аудиофайл нота за нотой, параллельно обновляя матрицу весов, как было описано выше. Пошаговая обработка MIDI-файла обеспечивается за счет встроенного инструмента Java под названием Sequencer.
public Learn(String midiName) {
try {
Sequence sequence = MidiSystem.getSequence(new File(midiName));
int id[] = {0, 0, 0};
int nArr[][] = new int[2][2];
for(Track track : sequence.getTracks()) {
for(int i = 0; i < track.size(); i++) {
MidiEvent event = track.get(i);
MidiMessage message = event.getMessage();
if(message instanceof ShortMessage) {
ShortMessage sm = (ShortMessage) message;
if(sm.getCommand() == NOTE_ON) {
int key = sm.getData1();
for(int j = 0; j < 2; j++) {
if(id[j] == 2) {
id[j] = 0;
Score.updateWeight(nArr[j][0], nArr[j][1], key);
} else {
nArr[j][id[j]++] = key;
}
}
}
}
}
}
cnt++;
} catch(InvalidMidiDataException|IOException e) {
e.printStackTrace();
}
}
Выбор правильной ноты
Ура! Мы дошли до самой важной части! Все строки кода, представленные выше, будут бесполезны, если мы не найдём способ генерировать правильную ноту. Процесс довольно прост и основан на случайных величинах: текущем состоянии (последние две ноты последовательности) и матрице переходов, полученной ранее. Вероятность генерируется случайно, с помощью функции Java Math.random(). Затем алгоритм просматривает матрицу переходов и возвращает ту вероятность, которая совпала (или оказалась наиболее близка) с вероятностью, сгенерированной функцией Math.random().
public static int nextNote(int n1, int n2) {
double rnd = Math.random();
double sum = 0.0;
for(int i = 0; i < 128; i++) {
sum += scoreMatrix[n1*127+n2][i];
if(sum >= rnd)
return i;
}
return (int) (rnd*127); /* In an off chance that no states are found (all have 0.0 probability of transition), the algorithm continues randomly */
}
Воспроизведение результата
Результат воспроизводится с помощью Synthesizer – встроенного инструмента Java, ноты для которого выбираются «на лету» из матрицы переходов по алгоритму, описанному выше. По большому счету, результат определяется двумя начальными нотами, сгенерированными случайным образом или выбранными пользователем.
try {
Synthesizer synth = MidiSystem.getSynthesizer();
synth.open();
final MidiChannel[] channels = synth.getChannels();
int fn, sn, nn;
fn = n1;
sn = n2;
while (!this.isInterrupted()) {
nn = Score.nextNote(fn, sn);
int octave = (nn/12)-1;
String noteName = NOTE_NAMES[nn%12];
channels[0].noteOn(nn, Info.NOTE_VELOCITY);
Thread.sleep(Info.NOTE_PAUSE);
channels[0].noteOff(nn);
fn = sn;
sn = nn;
}
} catch(Exception e) {}
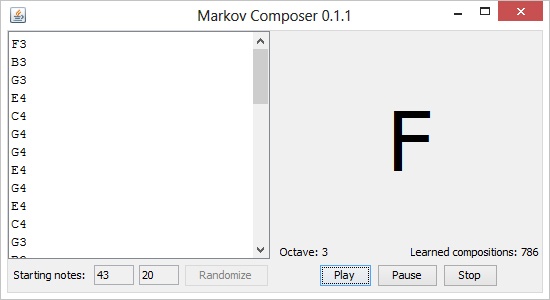
Конечный продукт (альфа-версия)
На изображении ниже представлен интерфейс приложения:
Сэмплы
Вот примеры композиций, созданных программой Markov composer. На основании проведенных экспериментов, должен сказать, что она способна создавать более длительные и интересные композиции.
Кода
Хотя это просто эксперимент, на выходе программы получается не полная дисгармония, а некоторые начальные комбинации могут привести к удивительным, приятно звучащим композициям.
Полный код программы, включая графический интерфейс, доступны в моем репозитории на GitHub.
Автор: Audioman







