В своей последней статье я рассматривал вопрос того, как нужно строить музыкальную теорию на основании эмпирического наблюдения за людьми – на базе их вкусов и музыкальных предпочтений. Также для построения музыкальной теории можно попытаться понять, что же происходит у нас в голове. Этот вопрос рассмотрел Дэниел Уилкерсон (Daniel Shawcross Wilkerson) в своей статье «Разъяснение гармонии: По пути прогресса к научной теории музыки». Это эссе имеет второе очаровательное старомодное название:
Мажорная гамма, стандартная терминология и различия в восприятии минорных и мажорных трезвучий, которые объясняются основными принципами физики и математики. Несостоятельность теории Гельмгольца, а также обоснование теории Терхардта и других.
Уилкерсон начинает с замечания о том, что книги по теории музыки читаются как медицинские тексты средних веков и «в них полно необоснованных суждений с забавными символами, приукрашенными фразами на латыни». Мы можем писать их понятнее.
Уилкерсон предполагает, что теорию гармонии необходимо выстраивать на понимании работы , а в частности того, как он обрабатывает аудиосигналы. В ходе нашей эволюции мы приобрели способность распознавать звуки с естественными гармониками, потому что обычно они поступают из известных нам источников, примером могут служить глотки других животных. Музыкальная гармония – это придуманный нами способ порадовать свои распознаватели гармонических рядов.
Насколько хорошо мы можем воспринимать гармоники звука? Настолько хорошо, что если мы слышим отрывки ряда обертонов, мы с легкостью и абсолютно бессознательно можем дополнить его отсутствующими обертонами. Например, если мы слышим гармонический ряд, в котором отсутствует основной тон, то мы автоматически дополняем им последовательность. В частности, когда мы слышим созвучие нескольких тонов, то мы можем вычислить наибольший общий делитель их частот и будем считать его общим тоном. Этот феномен «мнимого тона» дает возможность различать басовую партию, слушая музыку в крошечных наушниках. Даже при том, что размер динамика недостаточно велик для воспроизведения баса, мы экстраполируем его из обертонов.
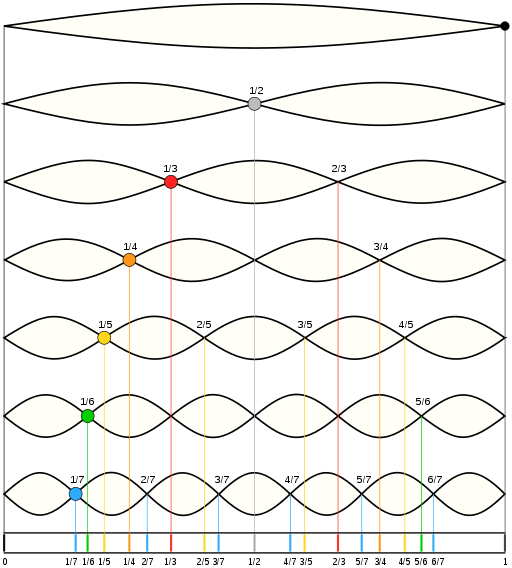
Идея состоит в том, что наш обладает специальными детекторами гармонического ряда, которые помогают различать равнозначность октав.
В то время как тональности различных гармонических рядов различаются, отношение их частот к основной частоте остается постоянным всегда. Поэтому мы считаем, что проводит нормализацию тонов путем их деления и получает некоторые их соотношения. Обработка звука требует проведения анализа частот, отличающихся друг от друга на несколько порядков. Если эти частоты могут быть полностью проанализированы, то у нас появляется возможность использовать эти знания повторно. Рассмотрим концептуально простой процесс, когда сокращает или увеличивает вдвое частоту волны, пока это значение не попадет в определённый диапазон.
Теперь нужно что-то для распознавания тонов гармонического ряда в диапазоне частот, не превышающих тон в два раза, а не на всем звуковом спектре. Таким образом, проблема разбивается на две подзадачи, где первая – это нормализация, а вторая – это непосредственно распознавание, что значительно упрощает конструкцию результирующего распознавателя. Поэтому мы считаем, что, вполне вероятно, наш нормализует тона, сокращая вдвое или удваивая их до тех пор, пока они не попадут в определенный диапазон частот, разнящихся на два порядка. Также вполне вероятно, что делит пополам или удваивает частоты на различные степени двойки параллельно, а затем проводит одновременное их распознавание. Если какая-нибудь частота совпадает [с базовым диапазоном], нужная гармоника найдена.
Так почему же нам нравится гармония? Уилкерсон говорит, что она сводится к искусственному усилению естественного ряда обертонов. Слышать аккорд – все равно что слышать волшебный голос с более сильными и чистыми гармониками, чем у отдельного [естественного] источника звука. Уилкерсон как-то выразился, что гармония для нас «слаще сладкого».
Ниже представлена иллюстрация того, что имел в виду Уилкерсон. На рисунке изображена спектрограмма двух нот, сыгранных на скрипке: нота С («до») слева и G («соль») справа.
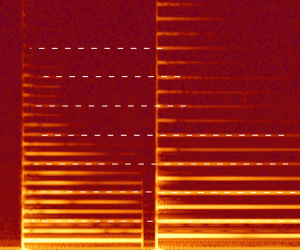
Пунктирными линиями отмечены ноты, которые имеют практически одинаковый спектр. Каждому обертону из C можно найти похожий в ноте G. Если вы проиграете эти ноты одновременно, то гармонический распознаватель в вашем тут же активизируется и отметит поразительное соответствие.
Это хорошее объяснение созвучия. Но мы также любим и не консонантные гармонии. Что думает Уилкерсон на этот счет? Он списывает это на нашу врождённую любовь к повествованиям, сравнив последовательность аккордов с сюжетом произведения.
Если понимать и прогнозировать сюжетную линию рассказа довольно легко, то история кажется скучной, а если слишком сложно, то история получается сумбурной. Если удерживать сюжет между двумя этими крайностями, получается интересная история. Простота исходит от «темы» рассказа, его основной мысли, а неоднозначность – это отсутствие простого объяснения или «темы», вследствие чего возникают сложности.
Раскрыть тему в самом начале – способ избавиться от сложности еще в зародыше. Вероятно, ответвления от темы и необъяснимая остаточная сложность «считываются» нашим с помощью «обработчика ожиданий». Искусство управления гармонией – это, по большей части, просто игра с обработчиком ожиданий, когда вы даете ему такое количество сложности, чтобы начальная информация оставалась в интересной зоне: между чем-то очевидным и чем-то бессмысленным.
Далее давайте посмотрим, что думает Уилкерсон о том, как мы получаем простую диатоническую гармонию из естественного ряда обертонов. Мы начинаем с поиска идеального гармонического ряда состоящего из одной ноты, скажем C4 – «до» четвертой октавы («до» первой октавы на пианино) и соотносим его с целой октавой путем деления частоты по мере необходимости.
Я последую условностям Уилкерсона и буду считать фундаментальной первую гармонику:
- Вторая гармоника имеет частоту вдвое большую, чем С4, получается нота С5 – «до» второй октавы.
- Третья гармоника с частотой втрое большей, чем С4 – это G5. Когда вы делите её частоту на два, вы получаете G4 – чистую квинту «до»-«соль» первой октавы.
- Четвертая гармоника с частотой, в четыре раза превышающей С4 – это С6. На самом деле, все четные гармоники – это просто нота С («до»), транспонированная на две октавы выше.
- Пятая гармоника с частотой, в пять раз превышающей С4 – это E6. Нормализовав её, получаем E4 – большую терцию «до»-«ми» первой октавы.
Итак, первые несколько естественных гармоник содержат большую терцию и ноты C, E, G («до», «ми», «соль»), плюс ноту «до», транспонированную на несколько октав выше. Выбрав в качестве фундаментальной другую гармонику, вы получите те же самые соотношения между частотами.
Далее, Уилкерсон просит нас построить другое мажорное трезвучие, основанное на ноте в серии обертонов, наиболее близких к основному тону. Первая нота, которую вы получаете из гармоник ноты С (не считая С на октаву выше) – это G («соль»). Если вы строите мажорное трезвучие на основании ноты G, вы получаете ноты G, B и D («соль», «си» и «ре»). Затем Уилкерсон хочет, чтобы мы построили мажорное трезвучие от ближайшей ноты, у которой третьей гармоникой является нота С. Этой нотой является F («фа») и её мажорное трезвучие воспроизводится из серии обертонов F, A и C («фа», «ля» и «до»). Проранжировав все эти ноты в соответствии с частотой, вы получите последовательность C, D, E, F, G, A, B – то есть всем известную мажорную гамму.
Как только вы получаете этот набор нот, вы можете вывести из них все виды других интересных аккордов и гамм. Используя ноты D, E или A («ре», «ми» или «ля») в качестве базиса, вы получите минорные трезвучия. Наша эмоциональная реакция на минорные аккорды более сложная, чем просто «Ага!», как в случае с узнаванием мажорных. Минорное трезвучие A («до»-«ми»-«ля») обладает теми же парными интервалами гармонического ряда: квинтой между A и E («ля» и «ми») и большой терцией между C и E. Но мы не слышим сам гармонический ряд. Уилкерсон считает, что мы находим минорные аккорды более интересными, из-за того, что мы узнаем их лишь частично, и они дразнят наш внутренний распознаватель гармонических рядов.
В дальнейшем теория подкрепилась тем, что существует только один мажорный ряд, в то время как минорных рядов множество. Напомню, что в мажорном ряду, построенном из мажорного трезвучия, все звучит понятно для человеческого уха, тогда как звучание минорных рядов, построенных из минорного трезвучия, часто кажется неправильным и неоднозначным.
На устранение неоднозначности расходуется множество наших умственных ресурсов – это, в сущности, поиск наиболее вероятного и логичного объяснения расплывчатой и противоречивой информации о мире. В этом мы отличаемся от компьютеров и превосходим их в некоторых жизненных ситуациях. Музыка дразнит участок нашего , отвечающий за разрешение неоднозначных ситуаций, вызывая у нас легкоузнаваемые образы с неочевидными значениями.
Уилкерсон уподобляет сложную гармонию рисункам в стиле кубизма:
Части объекта могут быть изображены достаточно достоверно, так что их легко распознать, однако объект в целом нарисован непонятно. Возникает интересный эффект: мы распознаем объект по отдельным особенностям, которые улавливает наше восприятие, однако у нас все равно возникает чувство, что мы видим предмет не в своей естественной форме, а в форме беспорядочной, неуместной или неясной.
Что же насчет более сложных аккордов? Уилкерсон говорит, что здесь применима логика, которой мы воспользовались при объяснении влияния минорных аккордов.
хочет слышать определённую гармоническую последовательность. Если мы будем «пропускать» [в нашей последовательности] все больше и больше нот, а будет стараться восполнить все больше и больше пропусков, то достаточно скоро настанет такой момент, когда воспроизводимых нот будет едва хватать, чтобы распознать гармонический ряд. Что если сыгранных нот окажется недостаточно, чтобы его определить? Значит ли это то, что пропуски гармонических рядов можно будет заполнить более, чем одним способом?
Некоторые аккорды неоднозначны и поэтому неустойчивы. Если у будет более, чем один альтернативный вариант заполнения пропусков, то звук будет «нестабилен» до тех пор, пока исполнитель не предоставит достаточное количество нот, способных «сломать несоразмерность» и неоднозначность ряда.
Если вы слышите ноты C, F и G («до», «фа» и «соль»), вы слышите что-то похожее на какой-то естественный ряд обертонов. Но на который из них? Как C («до»), так и F («фа») могут выступать в качестве основного тона. Музыканты называют такие ситуации «подвешенным аккордом», что довольно точно описывает ситуацию. Вы как бы находитесь в подвешенном состоянии между двумя допустимыми ситуациями, в которых или C или F могут выступать в качестве основных нот. Если заменить F на E («ми»), то ситуация будет разрешена в пользу C, а если G заменить на A («ля»), то в пользу F. В более современной музыке такая ситуация может не разрешиться вообще.
Идея неоднозначности отлично объясняет любой из экзотических аккордов. Когда вы слышите увеличенное или уменьшенное трезвучие или джазовый аккорд с множеством «дополнительных» нот, то вам слышатся парные интервалы, которые созвучны с рядом обертонов. Но вы не слышите законченный обертоновый ряд, а, возможно, слышите более одного такого ряда. Результат доставляет меньше удовольствия, чем мажорный аккорд, но он все равно звучит как что-то значительное, нужно просто приложить усилие, чтобы понять, что происходит.
Вероятно, имеет один модуль разрешения многозначности, который работает и в вербальном общении, и в других ситуациях, как в случае с музыкой. Таким образом, несмотря на то, что аккорды могут звучать странно по отдельности, музыкальная тема, предваряющая эти аккорды, может привнести в них определенный смысл. Вспомните стандартную структуру шутки: история (создание темы), а затем изюминка. Изюминка не будет смешной без контекста, который дает нам история, но мы связываем саму шутку именно с изюминкой, и не учитываем историю, которая сделала эту шутку возможной.
Теория Уилкерсона и стандарты классической теории согласуются в том, что гармонический ряд – это сердце и душа гармонии. Тем не менее, есть несколько моментов, в которых эти теории расходятся. Например, Уилкерсон отвергает квинтовый круг как метод достижения гармонии, но не отвергает всего, что освещает принципы природы музыки.
Квинтовый круг – это отвлекающий маневр, который не дает людям, понять гармонию, осознать, насколько хорошо она звучит.
Мне очень нравится теория Уилкесона, но в одном месте он сильно ошибается – речь идет о его анализе тритона.
Звучание нот C и F# («до» и «фа-диез») на фортепиано просто ужасно. Этот интервал также называется тритоном, так как расстояние между C и F# – это три целых тона (где под словом «тон» имеется в виду расстояние из двух полутонов – в совокупности три тона – это шесть полутонов). Мы можем проанализировать, почему этот интервал звучит так неустойчиво: отношение между [частотами] F# и C не соответствует ни одной гармонике гармонического ряда. Этот интервал заслуженно получил свое название «интервал дьявола».
Уилкерсон проделал большую работу, чтобы оградить свои взгляды от влияния Евроцентрического музыкального окультуривания, но здесь он позволил себе немного отклониться. Те из нас, кто любит блюз и его музыкальных наследников, не станут называть звучание тритона ужасным. Его звук, конечно, не столь приятный, как у квинты или большой терции, но чуть менее приятный звук – не значит плохой. Уилкерсон мог бы объяснить тритон лучше, прибегнув к собственным идеям о неоднозначности и сложности. Тритон – более «взрослый» звук, и его нельзя найти в рамках ряда обертонов, но можно легко получить из интервала, который может там находиться. В до-мажоре существует тритон между F и B («фа» и «си»).
Как один из множества музыкальных теоретиков, Уилкерсон может много что рассказать о гармонии и почти ничего не говорит про ритм. Но у него можно найти вот этот замечательный маленький абзац:
Недавно, слушая вечером звуки, издаваемые насекомым, я был поражен тем, как в них появлялся ритм по мере «наслаивания» угасающей музыкальной «темы» на новую, более сложную последовательность звуков. Сначала я слышал простой предсказуемый ритм, и вдруг, вопреки ожиданиям, ритм сменился, зазвучав «поверх» основной темы. Явления повествования, прогнозирования и предсказания темы можно отнести как к гармонии, так и к ритму. Феномен ожидания как бы обобщает входные данные, и поэтому ожидание гармонии должно работать в схожей манере с ритмическим ожиданием.
Как гармония – идеализированная абстракция человеческого голоса, так и ритм – идеализированная абстракция физических движений, танцев. Я бы хотел продвинуть теорию Уилкерсона на шаг дальше. Нота – это просто очень быстрый ритм, а аккорды – это очень быстрые полиритмы. Как ритм является основой музыки в целом, так и наша теория ритма должна быть основой нашей теории музыки.
Автор: dmitrykabanov
