Пару лет назад мне попалась интересная статья о взаимосвязи цен на золото и нефть.
И я решил немного расширить модель и провести собственное исследование.
Прежде всего — взять не два товара, а некий более существенный набор.
После долгих поисков по интернету, я нашел этот сайт, с которого скачал архив цен (скачать XLS) на товары за 35 лет.
Все данные я обрабатывал в MATLAB.
xls = xlsread('data.xls'); %загружаем данные из файла XLS
time = 1:399; %индекс
real_time = 1979 + time/12; %реальная дата
data = xls(time,1:22);
% получаем данные:
oil = data(:,1); % нефть
gold = data(:,2); % золото
iron = data(:,3); % железная руда
logs = data(:,4); % бревно
maize = data(:,5); % кукуруза
beef = data(:,6); % говядина
% и все остальные товары
% добавляем в матрицу те товары, которые будем подвергать анализу:
all_goods = [oil gold logs maize beef chicken gas tea tobacco wheat sugar soy rice cotton copper coffee coal];
goods_count = size(all_goods, 2); % количество товаров
В качестве относительной цены для более чем двух товаров можно использовать цену, деленную на среднее геометрическое:
geom_average = ones(size(time))'; % для транспонирования в Матлабе используется символ '
%, но Хабр воспринимает его как начало строки
for i = 1:goods_count
geom_average = geom_average .* all_goods(:,i);
end
geom_average = geom_average .^ (1/goods_count); % среднее геометрическое
all_goods_rel = zeros(size(all_goods));
all_goods_norm = zeros(size(all_goods));
mean_ = zeros(1,goods_count);
std_ = zeros(1,goods_count);
percent_std_ = zeros(1,goods_count);
for i = 1:goods_count
all_goods_rel(:,i) = all_goods(:,i) ./ geom_average; % относительные цены товаров
mean_(i) = mean(all_goods_rel(:,i)); % среднее по времени
all_goods_norm(:,i) = all_goods_rel(:,i) / mean_(i); % относительные цены, нормированные на среднее по времени
std_(i) = std(all_goods_rel(:,i)); % стандартное отклонение по времени
percent_std_(i) = 100*std_(i)/mean_(i); % стандартное отклонение в процентах
end
Графики нормированных цен:
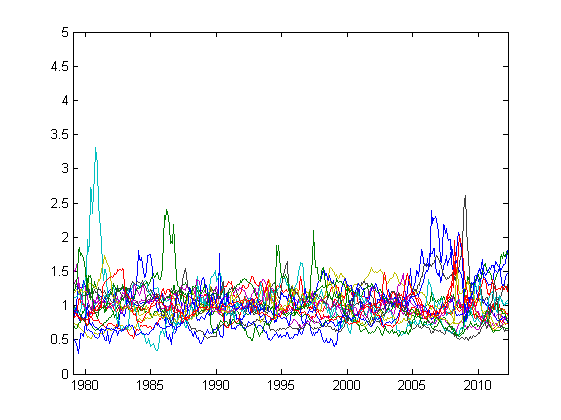
Стандартные отклонения относительных цен в процентах от среднего по времени:
| Сырая нефть | 37,77% | Газ | 32,18% | Рис | 19,71% |
| Золото | 21,57% | Чай | 25,18% | Хлопок | 24,52% |
| Бревно | 20,33% | Табак | 20,55% | Медь | 36,24% |
| Кукуруза | 15,71% | Пшеница | 14,58% | Кофе | 37,08% |
| Говядина | 19,39% | Сахар | 37,91% | Уголь | 21,68% |
| Куриное мясо | 25,47% | Соя | 12,68% |
Теперь попробуем составить диверсифицированный продукт (ДП).
Пусть x — вектор относительного количества товаров, sum(xi) = 1;
A — матрица ковариаций нормированных цен.
Тогда дисперсия диверсифицированного продукта вычисляется как X'*A*X;
Нам нужно ее минимизировать.
Типичная задача на условный экстремум, решается методом множителей Лагранжа.
Не буду вдаваться в подробности, решается так:
A = cov(all_goods_rel); % матрица ковариаций
cond = ones(1, goods_count);
B = [2*A cond']; %'
B = [B; [cond 0]];
b = [zeros(1, goods_count) 1]';
x = (B^-1)*b;
Состав ДП получается следующий:
| Сырая нефть | 0,0035 баррелей | Газ | 23,2 тыс. БТЕ | Рис | 310,3 г |
| Золото | 9,627 мг | Чай | 76,3 г | Хлопок | 98,1 г |
| Бревно | 0,353 куб. дм | Табак | 45,69 г | Медь | 45,79 г |
| Кукуруза | 970,2 г | Пшеница | 514,2 г | Кофе | 40,7 г |
| Говядина | 64,2 г | Сахар | 538,8 г | Уголь | 3,5 кг |
| Куриное мясо | 148,8 г | Соя | 416,5 г |
Вычислим стоимость ДП:
DP = all_goods_rel*x(1:goods_count); % стоимость относительно среднего геометрического
USD_per_DP = all_goods*x(1:goods_count); % стоимость в долларах
Построим графики:
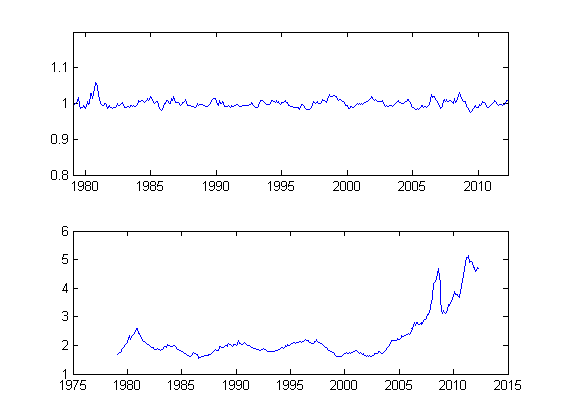
Сверху — график относительной стоимости, внизу — стоимость в долларах.
Стандартное отклонение относительной стоимости ДП за более чем 30 лет — всего 1.06%!
Но его стоимость в долларах выросла (соответственно покупательная способность доллара упала).
Так от чего же эта покупательная способность может зависеть?
Когда-то мне попадались данные о государственном долге США.
Здесь (стр. 143-144) я нашел подробные данные о государственном долге и перегнал их в файл XLS.
Получим данные из таблицы:
debt_xls = xlsread('usa_debt.xls');
debt_time = debt_xls(:,1);
end_index = size(debt_time,1);
start_index = (1:end_index)*(debt_time == 1978);
debt_time = debt_time(start_index:end_index);
debt_usd = debt_xls(start_index:end_index,2);
debt_percent = debt_xls(start_index:end_index,3);
debt_time = debt_time + 1; % данные о долге даны на конец года, что равносильно началу следующего
И попробуем построить графики:
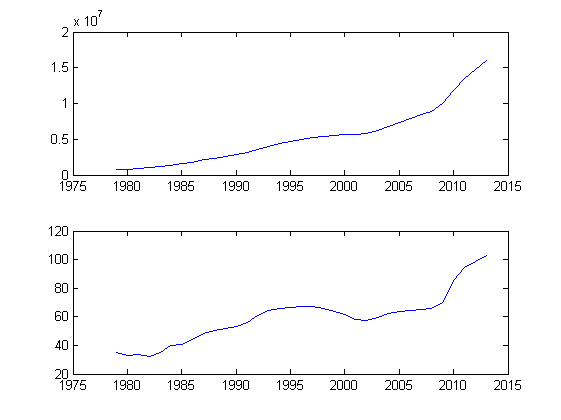
Верхний график — объем государственного долга США в миллионах долларов, нижний — в процентах от ВВП.
Можно заметить некоторое сходство в поведении объема долга в % ВВП и стоимости диверсифицированного продукта.
Так почему бы не попробовать наложить эти два графика друг на друга?
Для этого сгладим стоимость ДП скользящим средним, и интерполируем объем долга на весь временной интервал, а так же поделим на среднее по времени:
a = 1;
b = ones(1,24)/24;
debt_interp = interp1(debt_time, debt_percent, real_time, 'cubic')'; %'
USD_per_DP_mov_av = filter(b, a, USD_per_DP);
debt_and_DP = [USD_per_DP_mov_av/mean(USD_per_DP_mov_av) debt_interp/mean(debt_interp)];
debt_DP_corr = corr2(debt_and_DP(:,1),debt_and_DP(:,2))
figure;
plot(real_time, debt_and_DP);
Получаем следующую картину:
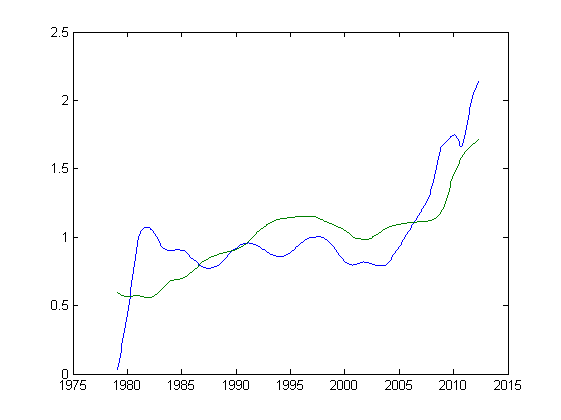
Можно так же вычислить коэффициент корреляции между стоимостью ДП в долларах и объемом долга, он равен 0.7165 или 71.65% — цифра довольно существенная.
Полностью matlab-скрипт можно посмотреть на github.
Послесловие
Как устроена экономика сегодня?
Как известно, большинство международных сделок совершается в долларах США.
Рубль так же привязан к доллару — ЦБ может эмитировать в экономику ровно столько рублей, сколько долларов поступило от экспорта, умножая эту сумму на курс доллара к рублю.
Что можно сделать?
Ввести понятие сбалансированной денежной единицы (СДЕ) и привязывать ее не к некоторой иностранной валюте, а к диверсифицированному продукту.
Реализовать это можно так:
Допустим имеется СДЕ и валюта некоторого иностранного государства V.
Курс СДЕ по отношению к V индексируется как стоимость ДП в валюте V, умноженная на некоторый коэффициент q.
Рассмотрим операции экспорта и импорта.
Допустим, 1V = 20СДЕ.
Экспорт.
Вариант 1.
Внешний покупатель закупает товар на сумму 1000V или 20000СДЕ в валюте V.
1000V «оседает» в ЦБ, 20000СДЕ эмитируется в экономику.
Вариант 2.
Внешний покупатель занимает у ЦБ 20000СДЕ и покупает на них товар.
То есть, по сути, обязуется в будущем вернуть равнозначное количество товара.
Импорт.
Вариант 1.
Внутренний покупатель закупает извне товар на сумму 1000V или 20000СДЕ в валюте V.
Центробанк выдает 1000V из своих резервов, 20000СДЕ из экономики изымается.
Вариант 2.
Внутренний покупатель закупает извне товар в СДЕ.
Заключение: введение СДЕ в теории позволяет практически избежать инфляции и ввести процентные ставки по кредитам, близкие к нулевым.
Автор: jatx






