Этот небольшой ликбез я опубликовал довольно давно в своем ЖЖ, но подумал, что здесь он найдет больше заинтересованных читателей.
Decentralized and Fixed-Structure H-infinity Control in MATLAB — так называется статья двух авторов (Pascal Gahinet и Pierre Apkarian), о которой я хочу рассказать здесь коротко.
Раз я решил писать для относительно широкой аудитории, предположим, что мы не знаем, что такое система управления. Тем, кому интересна сама тема поста — прокрутите, пожалуйста, текст до второй картинки.
От частного к общему сначала. Представим, что вам нужно наполнить ванну водой. Но такой, чтобы вам не было невыносимо холодно и обжигающе горячо. Предположим, что у вас шаровый смеситель, и вы просто поднимаете качалку вверх до упора, включая максимальный напор воды. Одной рукой вы начинаете проверять температуру воды. А другой двигать качалку влево-вправо, чтобы нужную температуру обеспечить себе. Вот это всё вместе — вы, ваш кран и температура воды — и есть система управления. У вас в голове есть представление о нужной вам температуре воды. Вы «измеряете» рукой ту, которую вам сейчас выдает кран. И другой рукой пытаетесь сделать так, чтобы разница между желаемой температурой и температурой воды из крана была минимальна. На картинке это можно изобразить так:
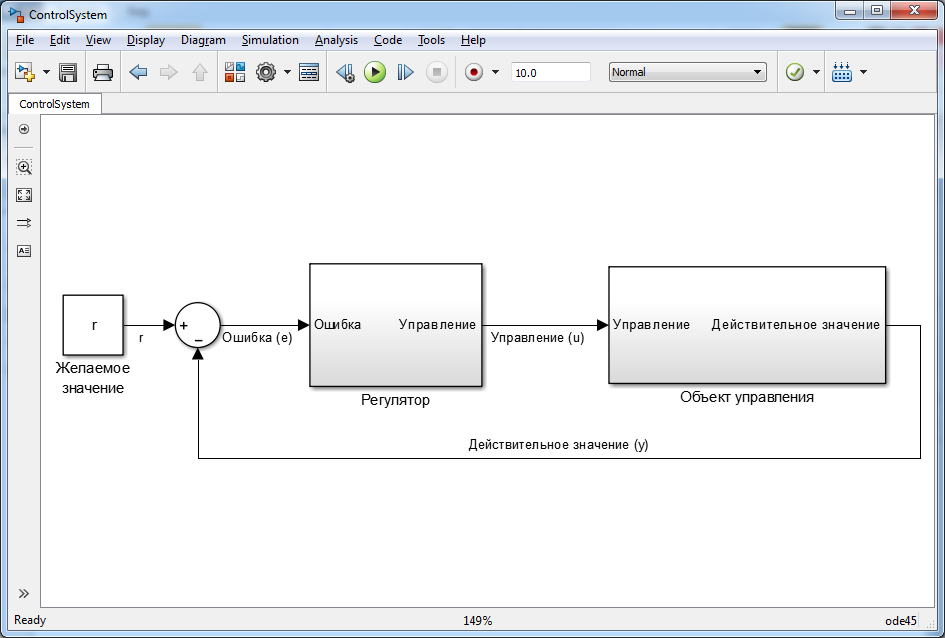
Рис. 1. Система управления в общем виде.
На самом деле, то, что мы нарисовали выше, фундаментальное представление системы управления с обратной связью. И на место объекта управления (в нашем случае — смеситель) может быть что угодно. И на месте регулятора (в нашем случае — человек) может быть что угодно.
На картинке для простоты датчик (в нашем случае — рука человека) не выносилась в отдельный блок, а включена в блок «Объект управления». Сам по себе объект не будет просто так говорит, какое у него сейчас значение параметра, который мы хотим менять. Также для простоты мы не стали выносить в отдельный блок исполнительное устройство (то, что нам помогает как-то воздействовать на объект управления — в нашем случае другую руку). Сам по себе объект тоже не станет просто так меняться: на него нужно чем-то влиять. Желаемое значение температуры мы берем из головы и называем его «теплая», хотя можем уточнить и сказать, что это, например, 20 градусов Цельсия. И вычитать из 20 то значение температуры, которое получаем при помощи датчика (нашей руки под струей воды). Так мы получим значение, называемое «ошибкой»: то, на сколько отличается температура воды из-под крана от нужной нам. И, при помощи регулятора (нашего , где мы понимаем, делать теплее или холоднее) будем делать так, чтобы этой разницы не было.
Когда-то люди подумали, что стоять у крана с водой (на самом деле это было довольно давно, и объектом было что-то другое) — не слишком интересное занятие. И решили как-то автоматизировать получение нужного значения (в нашем случае температуры, но мы помним, что это может быть что угодно). Поэтому стали появляться датчики (в начале механические — как, например, поплавок в, простите, сливном бачке унитаза, который «знает», сколько в бачке воды), потом электрические (например, термодатчик, который будет значение температуры преобразовывать в напряжение). А раз у нас есть какое-то электрическое значение, то почему бы не передать его в компьютер, который будет сам думать, как управлять чем-то. Мы ему просто скажем, какое значение мы хотим, а датчик будет ему говорить, какое на самом деле.
Так вот, немного закругляясь с ликбезом, задача человека, который разрабатывает систему управления, придумать такие правила для этого компьютера, чтобы желаемое значение за короткое время и без лишних колебаний приходило к нужному. Так как управлять иногда приходится не только температурой воды в кране, но и автомобилями, вертолетами, то это бывает довольно трудно сделать, поэтому просто логикой (поверни туда, если) не обойтись. А раз придется придумывать сложные уравнения для регулятора, то не плохо было бы такие уравнения иметь и для объекта (математическую модель объекта).
Совсем бывает сложно, когда управляемых величин много (много выходов), и возможностей управления много (много входов). Именно так, как в нашем примере.
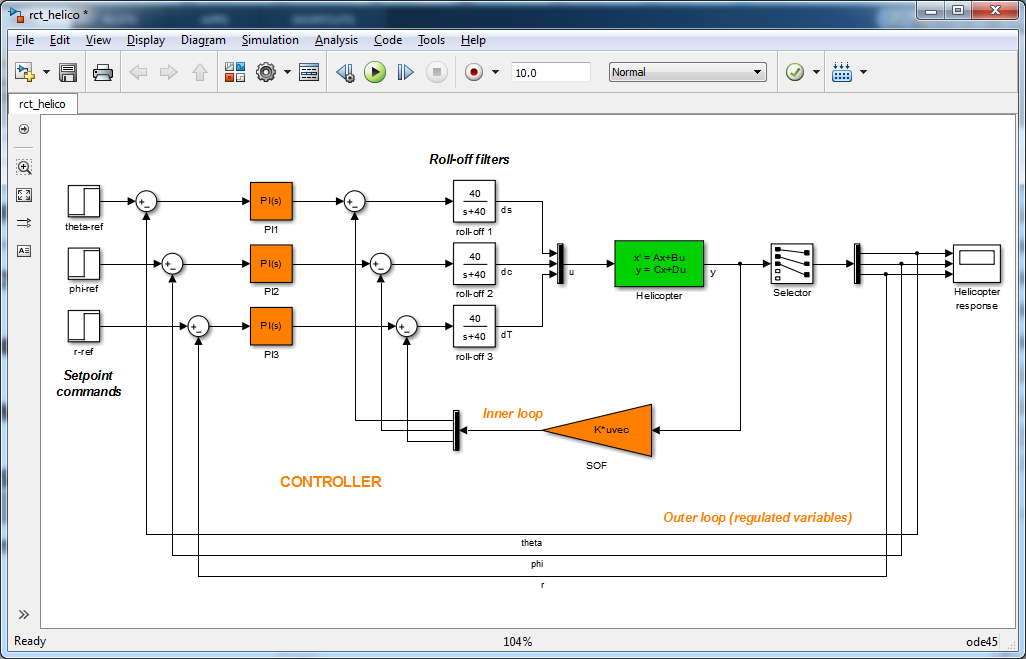
Рис. 2. Многоконтурная система управления вертолетом.
Здесь мы уже переходим к статье, на которую я дал ссылку в начале поста. У нас есть объект управления — вертолет (пожалуйста, посмотрите раздел 6 статьи, если интересно подробное описание). У нас есть три входных сигнала (на рис. 2 они показаны одной линией перед зеленым блоком State Space с названием u. И пять выходных сигналов (линия после зеленого блока с названием y). Мы выбрали такую структуру системы управления, что у нас есть три ПИ регулятора для управления тремя внешними контурами (оранжевые блоки PI с числительным в названии). И внутренний контур управления — для развязки каналов — с матрицей SOF (оранжевый треугольник).
Теперь дело за малым — задать требования к системе управления и как-то подобрать 21 параметр нашей системы управления. Авторы статьи предлагают технику, основанную на H-infinity. Но при этом инженеру для постановки задачи не требуется знать, что такое H-infinity (если совсем упрощенно). Мы задаем требования в частотной области, говорим, что настраивать нужно такие-то блоки в такой-то модели, что у нас есть управляющие сигналы и сигналы с датчиков. И запускаем алгоритм, который подробно описан в статье.
В MATLAB 2012a (и 2011b, но не в 2012b) есть пример, наглядно иллюстрирующий происходящее (фактически, мы можем повторить всё то, что происходит в статье). Чтобы открыть скрипт, можно исполнить команду edit helico_demo. Я позволил себе записать видео о том, как это работает и какие результаты мы получаем (опять же, просто повторив то, что указано в статье).
В итоге мы настраиваем 21 параметр и получаем устойчивую систему, которая решает поставленную задачу (развязка каналов и качество переходных процессов). Вставлять графики сюда не буду — посмотрите, пожалуйста, статью.
Буду рад комментариям.
Автор: URURU





