Данный материал создан ввиду прошедшей защиты выпускной квалификационной работы бакалавра, учитывающей некоторые замечания по объекту управления. Материал создаётся в качестве первоначального задела под возможную магистерскую диссертацию по той же тематике.
Современные системы магнитной левитации находят всё более и более широкое применение: высокоскоростные пассажирские поезда, изоляция чувствительных к вибрациям механизмов, магнитные подшипники, левитация расплавленного металла в индукционных печах, а также левитирование металлических заготовок. В последнее время эффект магнитной левитации также используют в бытовых устройствах.
Наиболее значимое применение, пожалуй, нашлось в поездах с системой левитации на сверхпроводниках. И это обусловлено такими преимуществами, как большая надёжность (из-за отсутствия трения), относительно низкое энергопотребление, способность развить большую скорость.
Однако из-за нелинейных уравнений движения объекта, описывающих его динамику, сложно воспроизводить процесс управления объектом. Речь пойдёт именно про положение (расстояние) объекта относительно нулевой отметки.
Если коротко, то магнитная левитация – это устойчивое положение объекта на определенном расстоянии в гравитационном поле, когда, как правило, ускорение свободного падения компенсируется ускорением объекта, которое создаётся магнитным полем. При этом возникает подъёмная сила.
Магнитная левитация реализуется с помощью диамагнетиков, систем вихревых токов и сверхпроводников, а также с помощью сервомеханизмов.
В текущем материале (под катом) будет рассмотрено модальное управление для линеаризованной системы магнитной левитации, а также реализация модального управления для нелинейной модели системы.
Математическая модель
Рассмотрим простую схему магнитной левитации.
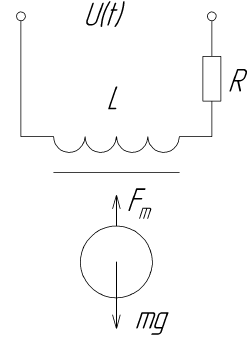
На данной схеме приведён электромагнит, который взаимодействует с магнитным полем объекта управления, который представляет собой шарик-постоянный магнит. Через изменение силы притяжения электромагнита и будет достигаться эффект левитации.
В выпускной работе рассматривался объект второго порядка, где в вектор состояния не был включён один важный компонент — ток в катушке. На этот раз данная компонента будет введена в рассмотрение.
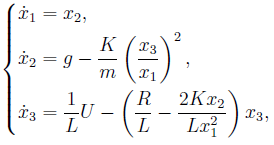
где 
— положение объекта;
— скорость изменения положения объекта;
— ускорение свободного падения;
— константа;
— масса объекта-шарика;
— ток в катушке;
— индуктивность катушки;
— входное напряжение;
— активное сопротивление катушки.
Значения некоторых приведённых выше переменных сведены в таблицу.
| K | m, кг | L, Гн | R, Ом |
| — | -------| ------|--------|
|0.000659|0.0106|0.109|31.3|
Чтобы получить линейную модель, следует провести линеаризацию системы уравнений.
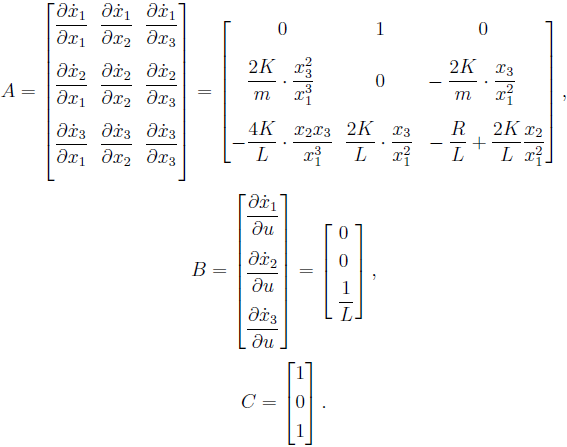
Вид матрицы 
можно обосновать тем, что рассмотрению подвержены такие переменные вектора состояния, как положение (
) и ток (
).
В таком виде полученные матрицы всё ещё не годятся для моделирования. Для этого зададимся начальными условиями.
Подставим теперь полученные данные и 
для нахождения значения входного сигнала в начальный момент времени:
Моделирование
Теперь можно синтезировать управление. Для исследований был выбран пакет Matlab. Ниже приведён код получения коэффициентов регулятора по состоянию:
matlab
g = 9.81;
K = 0.659*10^-3;
m = 0.0106;
L = 0.109;
R = 31.1;
x10 = 0.005;
x20 = 0;
x30 = sqrt(g*m/K)*x10;
u = R*x30;
A = [0 1 0;
2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2);
-4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)];
B = [0; 0; 1/L];
C = [1 0 0];
W = ctrb(A, B); % Матрица управляемости
detW = det(W);
poles = [-10 -10 -10]; % Полюса
K = acker(A, B, poles); % Регулятор
system = ss(A - B*K, B, C, 0); % Сборка модели
figure(1)
step(system) % тестовое воздействие
km = 1/dcgain(system); % масштабирующий коэффициент
system_m = ss(A - B*K, B*km, C, 0);
figure(2)
step(system_m)Чтобы понять, можно ли синтезировать управление для полученной системы, нужно знать матрицу управляемости, по определителю которой и делается вывод:
matlab
>> detW
detW =
-7.5351e+07Определитель отличен от нуля, следовательно, линеаризованная система управляема.
Вектор poles — это вектор, который содержит в себе желаемые полюса линеаризованной системы магнитной левитации.
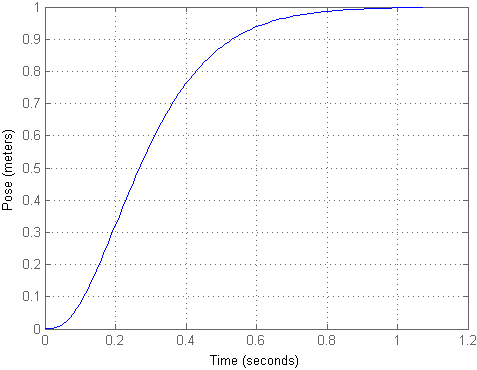
При подаче тестового воздействия в виде единичной ступеньки получаем следующий результат:
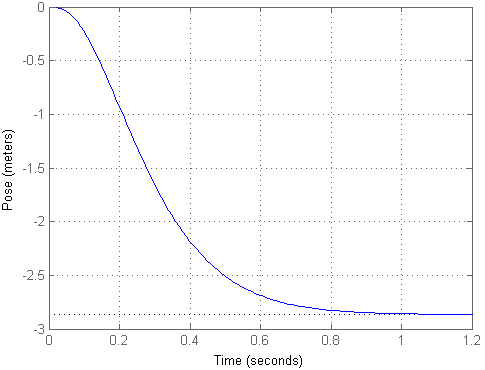
Как видно, получается, что объект улетел на довольно большое расстояние при небольшом воздействии, хотя и остался в одном положении. Чтобы вход соответствовал выходу, можно подсчитать масштабирующий коэффициент km и домножить на него входной сигнал, что и реализовалось во второй модели. Тогда переходный процесс будет выглядеть следующим образом:
Получающееся положение всё равно велико для подобной установки. Пока оставим без внимания ток и перейдём непосредственно к моделям Simulink, где рассмотрим оставшиеся вещи.
Масштабируем входной сигнал так, чтобы выходные значения было удобно представлять в сантиметрах. Подадим на вход несколько тестовых воздействий, чтобы проверить, как выглядят переходные процессы в системе, а также протекающий ток.
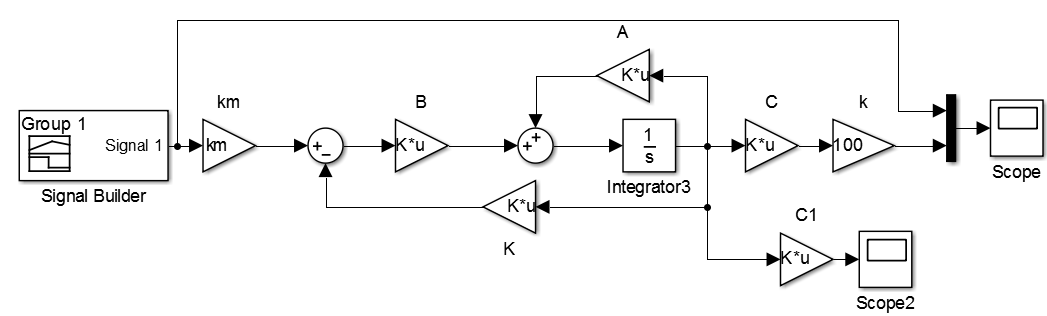
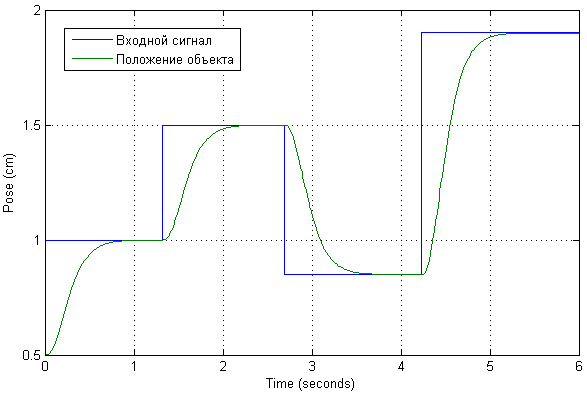
Получается, что величина тока при таких положениях объекта не столь значительна. Сами переходные процессы по положению имеют апериодический характер, без перерегулирования и статической ошибки. Собственно, так и было задано желаемыми полюсами скорректированной системы.
Однако это приближение в рабочей точке может некорректно сработать с исходной нелинейной моделью. Проверим это. Нелинейная модель системы с подключённым регулятором приведена ниже.
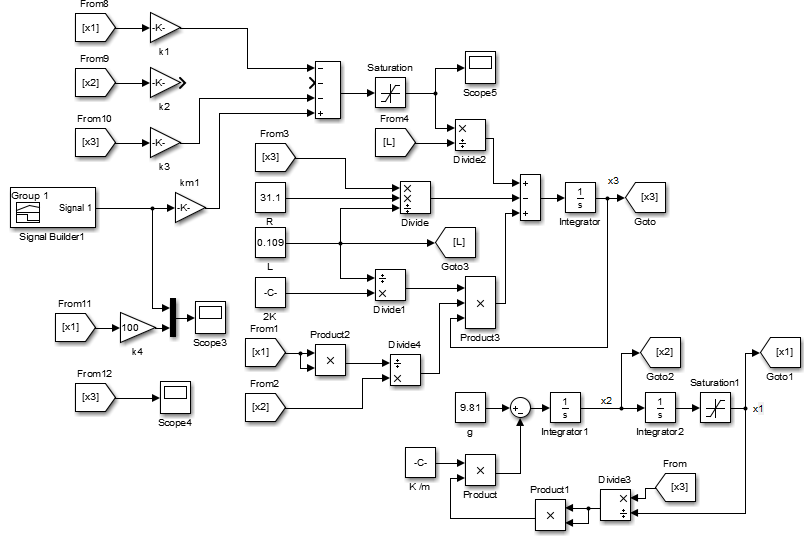
Это уже окончательный вариант, оставленный после всех экспериментов. Были установлены ограничения на входное напряжение (0-12В) и само положение объекта (0-4см). Вторая составляющая регулятора была исключена, поскольку с ней переходный процесс был неустойчив:
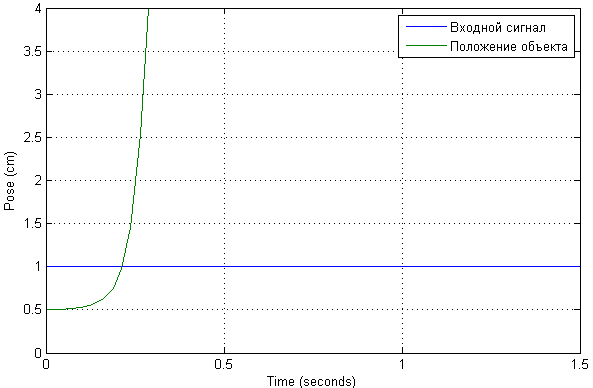
После изменений в схеме переходные процессы теперь выглядят так:
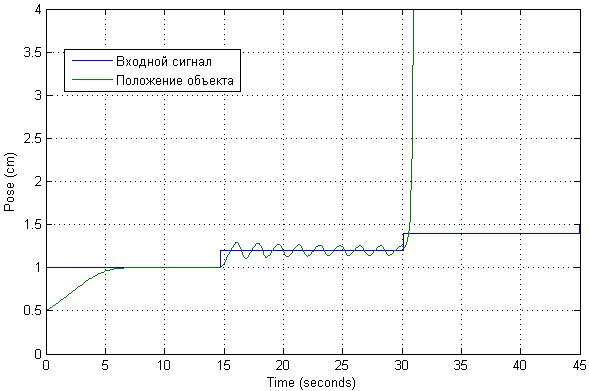
Был сразу проверен возможный диапазон работы такой системы. Можно увидеть, что нужное положение будет достигаться при незначительных отклонениях от начальной точки. При этом возможно проявление существенной колебательности.
При этом величина тока выглядит следующим образом:
Раз уже была проверка для нелинейной модели объекта, то можно и взглянуть, каким может быть максимальное значения положения для объекта, при котором он ещё не теряет устойчивости.
Проведя моделирование с разными входными сигналами, было замечено, что у линеаризованной модели всё очень даже хорошо. Так что здесь будут продемонстрированы переходные процессы по изначальному входному сигналу, увеличенному в 10 раз.
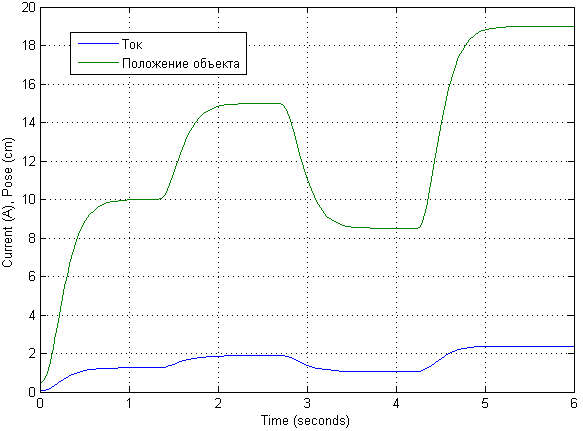
Сама математическая модель могла бы выглядеть несколько иначе. Её описание взято из описания математической [модели](http://www.ijens.org/Vol_13_I_01/136801-4747-IJECS-IJENS.pdf).
Заключение
Модальное управление для нелинейного объекта совсем не годится для каких-либо практических нужд. Следует рассмотреть иные реализации для данной системы магнитной левитации.
По части бакалаврской работы автором была реализована простенькая установка по левитации, о которой будет отдельно расписано в дальнейшем.
Автор: AlexEra
