Линеаризованная расходная характеристика паровой турбины. Часть 2. Пример построения для турбины ПТ-80 в MATLAB

Предисловие к первой части

Моделирование паровых турбин — повседневная задача сотен людей в нашей стране. Вместо слова модель принято говорить расходная характеристика. Расходные характеристики паровых турбин используют при решении таких задач, как вычисление удельного расхода условного топлива на электроэнергию и тепло, производимые ТЭЦ; оптимизация работы ТЭЦ; планирование и ведение режимов ТЭЦ.

Мною разработана новая расходная характеристика паровой турбины — линеаризованная расходная характеристика паровой турбины. Разработанная расходная характеристика удобна и эффективна в решении указанных задач. Однако на текущий момент она описана лишь в двух научных работах:

1. Оптимизация работы ТЭЦ в условиях оптового рынка электроэнергии и мощности России;
2. Вычислительные методы определения удельных расходов условного топлива ТЭЦ на отпущенную электрическую и тепловую энергию в режиме комбинированной выработки.

И сейчас в своем блоге мне бы хотелось:

• во-первых, простым и доступным языком ответить на основные вопросы о новой расходной характеристике (см. Линеаризованная расходная характеристика паровой турбины. Часть 1. Основные вопросы);
• во-вторых, предоставить пример построения новой расходной характеристики, который поможет разобраться и в методе построения, и в свойствах характеристики (см. ниже);
• в-третьих, опровергнуть два известных утверждения относительно режимов работы паровой турбины (см. Линеаризованная расходная характеристика паровой турбины. Часть 3. Развенчиваем мифы о работе паровой турбины).

1. Исходные данные

Исходными данными для построения линеаризованной расходной характеристики могут быть

1. фактические значения мощностей Q₀, N, Q_п, Q_т измеренные в процессе функционирования паровой турбины,
2. номограммы q_т брутто из нормативно-технической документации.

Конечно, фактические мгновенные значения Q₀, N, Q_п, Q_т являются идеальными исходными данными. Сбор таких данных трудоемок.

В тех случаях, когда фактические значения Q₀, N, Q_п, Q_т недоступны, можно обработать номограммы q_т брутто. Они, в свою очередь, были получены на основании измерений. Подробнее об испытаниях турбин читайте в Горнштейн В.М. и др. Методы оптимизации режимов энергосистем.

2. Алгоритм построения линеаризованной расходной характеристики

Алгоритм построения состоит из трех шагов.

1. Перевод номограмм или результатов измерений в табличный вид.
2. Линеаризация расходной характеристики паровой турбины.
3. Определение границ регулировочного диапазона работы паровой турбины.

При работе с номограммами q_т брутто первый шаг осуществляется быстро. Такую работу называют оцифровкой (digitizing). Оцифровка 9 номограмм для текущего примера заняла у меня около 40 минут.

Второй и третий шаг требуют применения математических пакетов. Я люблю и много лет использую MATLAB. Мой пример построения линеаризованной расходной характеристики выполнен именно в нем. Пример можно скачать по ссылке http://mbureau.ru/sites/default/files/Chuchueva-PT-80-linear-characteristic-curve.rar, запустить и самостоятельно разобраться в методе построения линеаризованной расходной характеристики.

Расходная характеристика для рассматриваемой турбины строилась для следующих фиксированных значений параметров режима:

• одноступенчатый режим работы,
• давление пара среднего давления = 13 кгс/см2,
• давление пара низкого давления = 1 кгс/см2.

Содержание архива Chuchueva-PT-80-linear-characteristic-curve.rar.

1) Номограммы удельного расхода q_т брутто на выработку электроэнергии (отмеченные красные точки оцифрованы — перенесены в таблицу):

• PT80_qt_Qm_eq_0_digit.png,
• PT80_qt_Qm_eq_100_digit.png,
• PT80_qt_Qm_eq_120_digit.png,
• PT80_qt_Qm_eq_140_digit.png,
• PT80_qt_Qm_eq_150_digit.png,
• PT80_qt_Qm_eq_20_digit.png,
• PT80_qt_Qm_eq_40_digit.png,
• PT80_qt_Qm_eq_60_digit.png,
• PT80_qt_Qm_eq_80_digit.png.

2) Результат оцифровки (каждому файлу csv соответствует файл png):

• PT-80_Qm_eq_0.csv,
• PT-80_Qm_eq_100.csv,
• PT-80_Qm_eq_120.csv,
• PT-80_Qm_eq_140.csv,
• PT-80_Qm_eq_150.csv,
• PT-80_Qm_eq_20.csv,
• PT-80_Qm_eq_40.csv,
• PT-80_Qm_eq_60.csv,
• PT-80_Qm_eq_80.csv.

3) Скрипт MATLAB с расчетами и построением графиков:

• PT_80_linear_characteristic_curve.m

4) Результат оцифровки номограмм и результат построения линеаризованной расходной характеристики в табличном виде:

• PT_80_linear_characteristic_curve.xlsx.

Шаг 1. Перевод номограмм или результатов измерений в табличный вид

1. Обработка исходных данных

Исходными данными для нашего примера являются номограммы q_т брутто.

Для перевода в цифровой вид множества номограмм нужен специальный инструмент. Я многократно использовала web-приложение http://arohatgi.info/WebPlotDigitizer/app/ для этих целей. Приложение просто, удобно, однако не имеет достаточной гибкости для автоматизации процесса. Часть работы приходится делать вручную.

На данном шаге важно оцифровать крайние точки номограмм, которые задают границы регулировочного диапазона работы паровой турбины.

Работа состояла в том, чтобы в каждом файле png при помощи приложения http://arohatgi.info/WebPlotDigitizer/app/ отметить точки расходной характеристики, скачать полученный csv и собрать все данные в одной таблице. Результат оцифровки можно найти в файле PT-80-linear-characteristic-curve.xlsx, лист «PT-80», таблица «Исходные данные».

2. Приведение единиц измерения к единицам мощности

Далее на листе «PT-80» рассчитываем значения Q₀ по формуле

$$display$$begin{equation} Q_0 = frac {q_T cdot N} {1000} + Q_П + Q_Т qquad (1) end{equation}$$display$$

и приводим все исходные величины к МВт. Расчеты реализованы средствами MS Excel.

Полученная таблица «Исходные данные (ед. мощности)» является результатом первого шага алгоритма.

Шаг 2. Линеаризация расходной характеристики паровой турбины

1. Проверка работы MATLAB

На данном шаге требуется установить и открыть MATLAB версии не ниже 7.3 (это старая версия, текущая 8.0). В MATLAB открыть файл PT_80_linear_characteristic_curve.m, запустить его и убедиться в работоспособности. Все работает корректно, если по итогам запуска скрипта в командной строке вы увидели следующее сообщение:

Значения считаны из файла PT_80_linear_characteristic_curve.xlsx за 1 сек
Коэффициенты: a(N) = 2.317, a(Qп) = 0.621, a(Qт) = 0.255, a0 = 33.874
Средняя ошибка = 0.006, (0.57%)
Число граничных точек регулировочного диапазона = 37

Если у вас возникли ошибки, то разберитесь самостоятельно, как их исправить.

2. Вычисления

Все вычисления реализованы в файле PT_80_linear_characteristic_curve.m. Рассмотрим его по частям.

1) Укажем название исходного файла, лист, диапазон ячеек, содержащий полученную на предыдущем шаге таблицу «Исходные данные (ед. мощности)».

XLSFileName = 'PT_80_linear_characteristic_curve.xlsx';
XLSSheetName = 'PT-80';
XLSRange = 'F3:I334';

2) Считаем исходные данные в MATLAB.

sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange);
N = sourceData(:,1);
Qm = sourceData(:,2);
Ql = sourceData(:,3);
Q0 = sourceData(:,4);
fprintf('Значения считаны из файла %s за %1.0f секn', XLSFileName, toc);

Используем переменную Qm для расхода пара среднего давления Q_п, индекс m от middle — средний; аналогично используем переменную Ql для расхода пара низкого давления Q_n, индекс l от low — низкий.

3) Определим коэффициенты α_i.

Вспомним общую формулу расходной характеристики

$$display$$begin{equation} Q_0 = f(N, Q_П, Q_Т) qquad (2) end{equation}$$display$$

и укажем независимые (x_digit) и зависимые (y_digit) переменные.

x_digit = [N Qm Ql ones(size(N,1),1)];        % электроэнергия N, промышленный пар Qп, теплофикационный пар Qт, единичный вектор
y_digit = Q0;                                 % расход острого пара Q0

Если вам непонятно, зачем в матрице x_digit единичный вектор (последний столбец), то читайте материалы по линейной регрессии. На тему регрессионного анализа рекомендую книгу Draper N., Smith H. Applied regression analysis. New York: Wiley, In press, 1981. 693 p. (есть на русском языке).

Уравнение линеаризованной расходной характеристики паровой турбины

$$display$$begin{equation} Q_0 = alpha_N cdot N + alpha_П cdot Q_П + alpha_Т cdot Q_Т + alpha_0 qquad (3) end{equation}$$display$$

является моделью множественной линейной регрессии. Коэффициенты α_i определим при помощи «большого блага цивилизации» — метода наименьших квадратов. Отдельно отмечу, что метод наименьших квадратов разработан Гауссом в 1795 году.

В MATLAB это делается одной строчкой.

A = regress(y_digit, x_digit);
fprintf('Коэффициенты: a(N) = %4.3f, a(Qп) = %4.3f, a(Qт) = %4.3f, a0 = %4.3fn',...
    A);

Переменная A содержит искомые коэффициенты (см. сообщение в командной строке MATLAB).

Таким образом, полученная линеаризованная расходная характеристика паровой турбины ПТ-80 имеет вид

$$display$$begin{equation} Q_0 = 2.317 cdot N + 0.621 cdot Q_П + 0.255 cdot Q_Т + 33.874 qquad (4) end{equation}$$display$$

4) Оценим ошибку линеаризации полученной расходной характеристики.

y_model = x_digit * A;
err = abs(y_model - y_digit) ./ y_digit;
fprintf('Средняя ошибка = %1.3f, (%4.2f%%)nn', mean(err), mean(err)*100);

Ошибка линеаризации равна 0,57% (см. сообщение в командной строке MATLAB).

Для оценки удобства использования линеаризованной расходной характеристики паровой турбины решим задачу вычисления расхода пара высокого давления Q₀ при известных значениях нагрузки N, Q_п, Q_т.

Пусть N = 82.3 МВт, Q_п = 55.5 МВт, Q_т = 62.4 МВт, тогда

$$display$$begin{equation} Q_0 = 2.317 cdot 82,3 + 0.621 cdot 55,5 + 0.255 cdot 62,4 + 33.874 = 274,9 qquad (5) end{equation}$$display$$

Напомню, что средняя ошибка вычислений составляет 0,57%.

Вернемся к вопросу, чем линеаризованная расходная характеристика паровой турбины принципиально удобнее номограмм удельного расхода q_т брутто на выработку электроэнергии? Чтобы понять принципиальную разницу на практике, решите две задачи.

1. Вычислите величину Q₀ с указанной точностью с использованием номограмм и ваших глаз.
2. Автоматизируйте процесс расчета Q₀ с использованием номограмм.

Очевидно, что в первой задаче определение значений q_т брутто на глаз чревато грубыми ошибками.

Вторая задача громоздка для автоматизации. Поскольку значения q_т брутто нелинейны, то для такой автоматизации число оцифрованных точек в десятки раз больше, чем в текущем примере. Одной оцифровки недостаточно, также необходимо реализовать алгоритм интерполяции (нахождения значений между точками) нелинейных значений брутто.

Шаг 3. Определение границ регулировочного диапазона работы паровой турбины

1. Вычисления

Для вычисления регулировочного диапазона воспользуемся другим «благом цивилизации» — методом выпуклой оболочки, convex hull.

В MATLAB это делается следующим образом.

indexCH = convhull(N, Qm, Ql, 'simplify', true);
index = unique(indexCH);
regRange = [N(index) Qm(index) Ql(index)];
regRangeQ0 = [regRange ones(size(regRange,1),1)] * A;
fprintf('Число граничных точек регулировочного диапазона = %dnn', size(index,1));

Метод convhull() определяет граничные точки регулировочного диапазона, заданного значениями переменных N, Qm, Ql. Переменная indexCH содержит вершины треугольников, построенных при помощи триангуляции Делоне. Переменная regRange содержит граничные точки регулировочного диапазона; переменная regRangeQ0 — значения расхода пара высокого давления для граничных точек регулировочного диапазона.

Результат вычислений можно найти в файле PT_80_linear_characteristic_curve.xlsx, лист «PT-80-result», таблица «Границы регулировочного диапазона».

Линеаризованная расходная характеристика построена. Она представляет собой формулу (4) и 37 точек, задающих границы (оболочку) регулировочного диапазона в соответствующей таблице.

2. Проверка

При автоматизации процессов расчета Q₀ необходимо проверять, находится ли некоторая точка со значениями N, Q_п, Q_т внутри регулировочного диапазона или за его пределами (режим технически не реализуем). В MATLAB это можно делать следующим образом.

Задаем значения N, Q_п, Q_т, которые мы хотим проверить.

n = 75;
qm = 120;
ql = 50;

Проверяем.

in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2));
in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3));
in = in1 && in2;
if in
    fprintf('Точка N = %3.2f МВт, Qп = %3.2f МВт, Qт = %3.2f МВт находится внутри регулировочного диапазонаn', n, qm, ql);
else
    fprintf('Точка N = %3.2f МВт, Qп = %3.2f МВт, Qт = %3.2f МВт находится снаружи регулировочного диапазона (технически недостижима)n', n, qm, ql);
end

Проверка осуществляется в два шага:

• переменная in1 показывает, попали ли значения N, Q_п внутрь проекции оболочки на оси N, Q_п;
• аналогично переменная in2 показывает, попали ли значения Q_п, Q_т внутрь проекции оболочки на оси Q_п, Q_т.

Если обе переменные равны 1 (true), то искомая точка находится внутри оболочки, задающей регулировочный диапазон работы паровой турбины.

Иллюстрация полученной линеаризованной расходной характеристики паровой турбины

Наиболее «щедрые блага цивилизации» нам достались в части иллюстрации результатов расчетов.

Предварительно нужно сказать, что пространство, в котором мы строим графики, т. е. пространство с осями x – N, y – Q_т, z – Q₀, w – Q_п, называем режимным пространством (см. Оптимизация работы ТЭЦ в условиях оптового рынка электроэнергии и мощности России

). Каждая точка этого пространства определяет некоторый режим работы паровой турбины. Режим может быть

• технически реализуемым, если точка находится внутри оболочки, задающей регулировочный диапазон,
• технически не реализуемым, если точка находится за пределами этой оболочки.

Если говорить о конденсационном режиме работы паровой турбины (Q_п = 0, Q_т = 0), то линеаризованная расходная характеристика представляет собой отрезок прямой. Если говорить о турбине Т-типа, то линеаризованная расходная характеристика представляет собой плоский многоугольник в трехмерном режимном пространстве с осями x – N, y – Q_т, z – Q₀, который легко визуализировать. Для турбины ПТ-типа визуализация наиболее сложная, поскольку линеаризованная расходная характеристика такой турбины представляет плоский многоугольник в четырехмерном пространстве (пояснения и примеры см. в Оптимизация работы ТЭЦ в условиях оптового рынка электроэнергии и мощности России, раздел Линеаризация расходной характеристики турбины).

1. Иллюстрация полученной линеаризованной расходной характеристики паровой турбины

Построим значения таблицы «Исходные данные (ед. мощности)» в режимном пространстве.

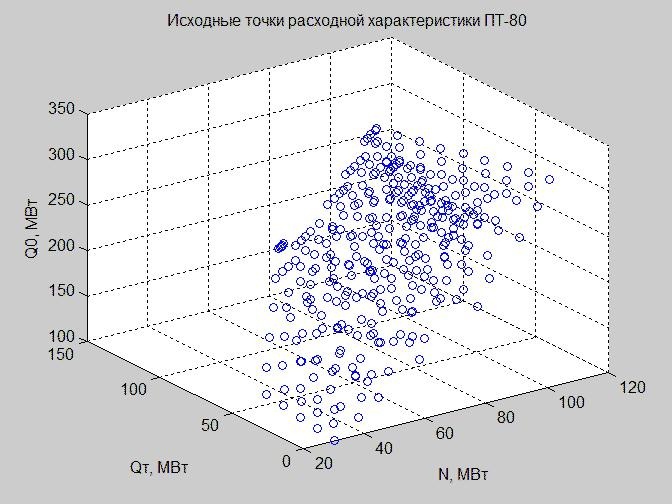
Рис. 3. Исходные точки расходной характеристики в режимном пространстве с осями x – N, y – Q_т, z – Q₀

Поскольку построить зависимость в четырехмерном пространстве мы не можем, до такого блага цивилизации еще не дошли, оперируем значениями Q_п следующим образом: исключаем их (рис. 3), зафиксируем (рис. 4) (см. код построения графиков в MATLAB).

Зафиксируем значение Q_п = 40 МВт и построим исходные точки и линеаризованную расходную характеристику.

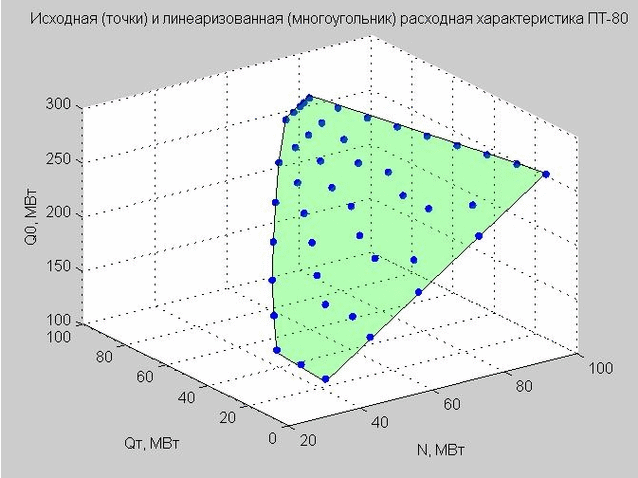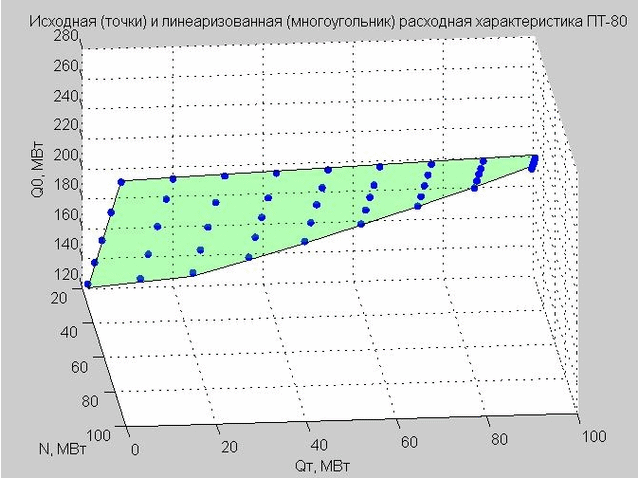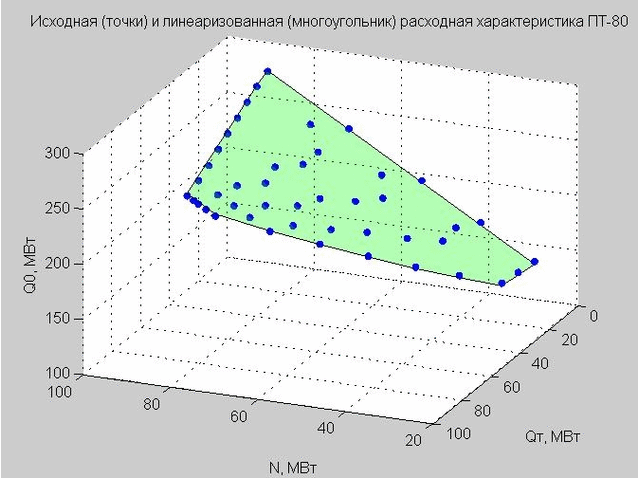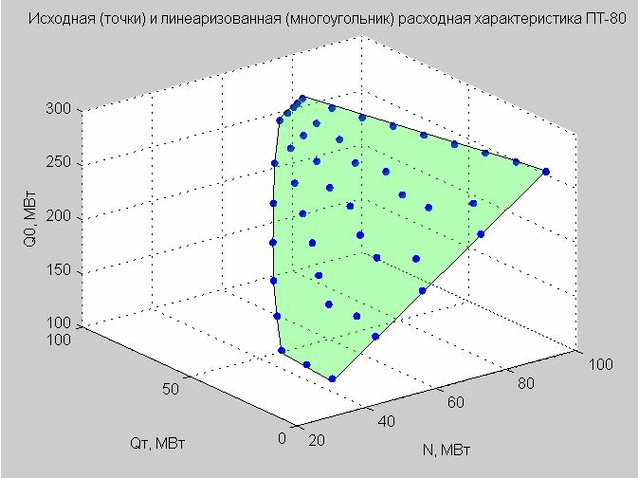
Рис. 4. Исходные точки расходной характеристики (синие точки), линеаризованная расходная характеристика (зеленый плоский многоугольник)

Вернемся к полученной нами формуле линеаризованной расходной характеристики (4). Если зафиксировать Q_п = 40 МВт МВт, то формула будет иметь вид

$$display$$begin{equation} Q_0 = 2.317 cdot N + 0.255 cdot Q_Т + 58.714 qquad (6) end{equation}$$display$$

Данная модель задает плоский многоугольник в трехмерном пространстве с осями x – N, y – Q_т, z – Q₀ по аналогии с турбиной Т-типа (его мы и видим на рис. 4).

Много лет назад, когда разрабатывали номограммы q_т брутто, на этапе анализа исходных данных совершили принципиальную ошибку. Вместо применения метода наименьших квадратов и построения линеаризованной расходной характеристики паровой турбины по неведомой причине сделали примитивный расчет:

$$display$$begin{equation} Q_0(N) = Q_э = Q_0 - Q_Т - Q_П qquad (7) end{equation}$$display$$

Вычли из расхода пара высокого давления Q₀ расходы паров Q_т, Q_п и отнесли полученную разницу Q₀(N) = Q_э на выработку электроэнергии. Полученную величину Q₀(N) = Q_э поделили на N и перевели в ккал/кВт·ч, получив удельный расход q_т брутто. Данный расчет не соответствует законам термодинамики.

Дорогие читатели, может, именно вы знаете неведомую причину? Поделитесь ею!

2. Иллюстрация регулировочного диапазона паровой турбины

Посмотрим оболочку регулировочного диапазона в режимном пространстве. Исходные точки для его построения представлены на рис. 5. Это те же самые точки, которые мы видим на рис. 3, однако теперь исключен параметр Q₀.

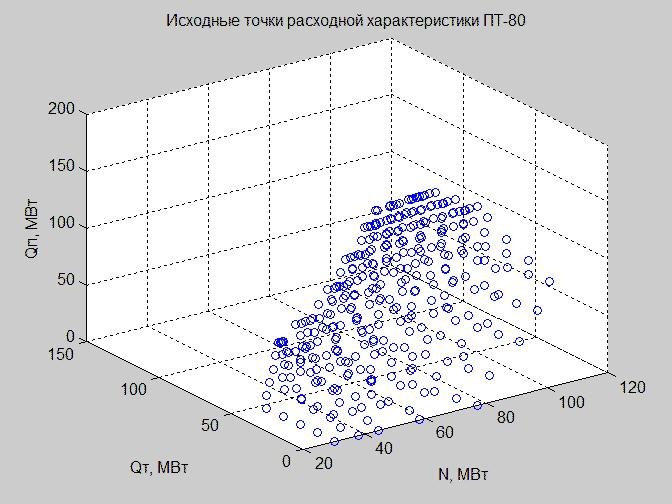
Рис. 5. Исходные точки расходной характеристики в режимном пространстве с осями x – N, y – Q_п, z – Q_т

Множество точек на рис. 5 является выпуклым. Применив функцию convexhull(), мы определили точки, которые задают внешнюю оболочку этого множества.

Триангуляция Делоне (набор связанных треугольников) позволяет нам построить оболочку регулировочного диапазона. Вершины треугольников являются граничными значениями регулировочного диапазона рассматриваемой нами паровой турбины ПТ-80.

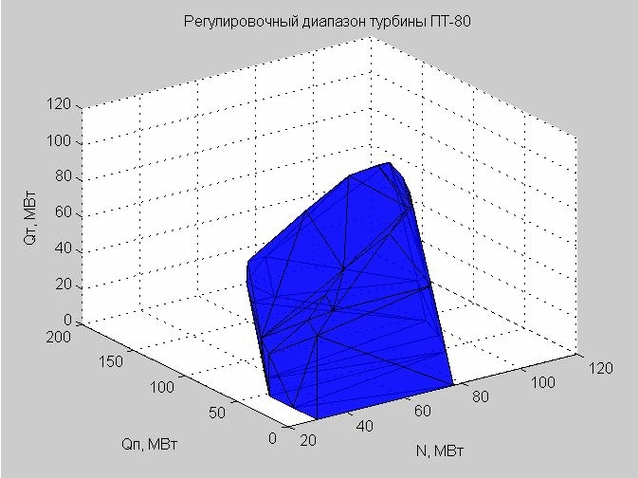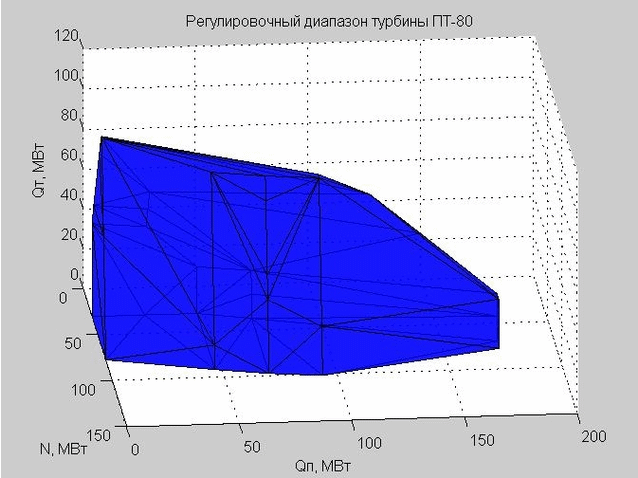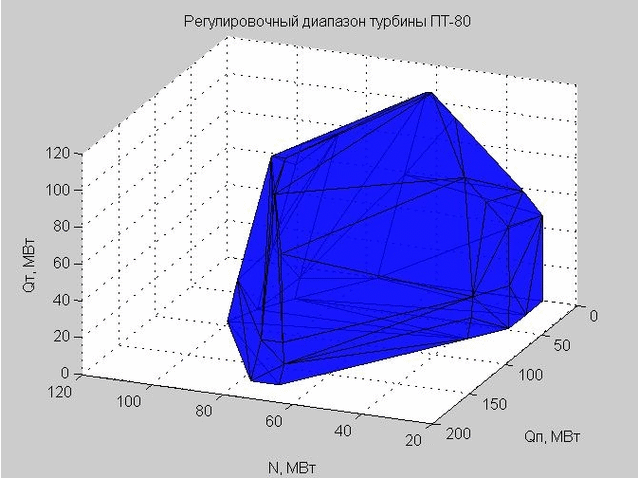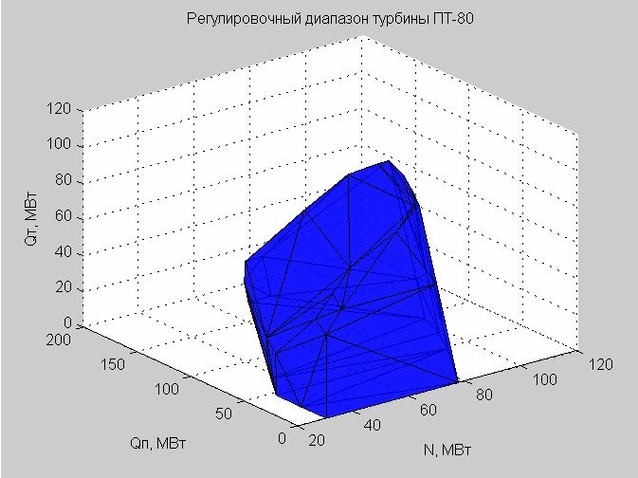
Рис. 6. Оболочка регулировочного диапазона, представленная множеством треугольников

Когда мы делали проверку некоторой точки на предмет попадания внутрь регулировочного диапазона, то мы проверяли, лежит ли эта точка внутри или снаружи полученной оболочки.

Все представленные выше графики построены средствами MATLAB (см. PT_80_linear_characteristic_curve.m).

Перспективные задачи, связанные с анализом работы паровой турбины при помощи линеаризованной расходной характеристики

Если вы делаете диплом или диссертацию, то могу предложить вам несколько задач, научную новизну которых вы легко сможете доказать всему миру. Кроме того, вы сделаете отличную и полезную работу.

Задача 1

Покажите, как изменится плоский многоугольник при изменении давления пара низкого давления Q_т.

Задача 2

Покажите, как изменится плоский многоугольник при изменении давления в конденсаторе.

Задача 3

Проверьте, можно ли представить коэффициенты линеаризованной расходной характеристики в виде функций дополнительных параметров режима, а именно:

$$display$$begin{equation} alpha_N = f(p_{0},...); \ alpha_П = f(p_{П},...); \ alpha_Т = f(p_{Т},...); \ alpha_0 = f(p_{2},...). end{equation}$$display$$

Здесь p₀ — давление пара высокого давления, p_п — давление пара среднего давления, p_т — давление пара низкого давления, p₂ — давление отработанного пара в конденсаторе, все единицы измерения кгс/см2.

Обоснуйте результат.

Ссылки

Чучуева И.А., Инкина Н.Е. Оптимизация работы ТЭЦ в условиях оптового рынка электроэнергии и мощности России // Наука и образование: научное издание МГТУ им. Н.Э. Баумана. 2015. № 8. С. 195-238.

• Раздел 1. Содержательная постановка задачи оптимизации работы ТЭЦ в России
• Раздел 2. Линеаризация расходной характеристики турбины
• Раздел 3. Формальная постановка задачи краткосрочной оптимизации работы ТЭЦ в условиях рыночной электроэнергетики
• Раздел 4. Вычислительный эксперимент
• Список литературы с комментариями
• Сравнение оптимизационных задач 1 и 2 при определении оптимального состава включенного оборудования

Чучуева И.А. Вычислительные методы определения удельных расходов условного топлива ТЭЦ на отпущенную электрическую и тепловую энергию в режиме комбинированной выработки // Наука и образование: научное издание МГТУ им. Н.Э. Баумана. 2016. № 2. С. 135-165.

• Раздел 1. Постановка задачи
• Раздел 2. Обзор методов
• Раздел 3. Новый метод расчета удельных расходов условного топлива
• Раздел 4. Сравнение методов
• Список литературы

Линеаризованная расходная характеристика паровой турбины.

• Часть 1. Основные вопросы
• Часть 2. Пример построения для турбины ПТ-80 в MATLAB
• Часть 3. Развенчиваем мифы о режимах работы паровой турбины

Автор: mbureau

Источник