Всем привет! В этой статье речь пойдет о реализации быстрого преобразования Фурье в формате с плавающей точкой на ПЛИС. Будут показаны основные особенности разработки ядра от самой первой стадии до готового конфигурируемого IP-ядра. В частности, будет проведено сравнение с готовыми ядрами фирмы Xilinx, показаны преимущества и недостатки тех или иных вариантов реализации. В статье будет рассказано о главной особенности ядра БПФ и ОБПФ — об отсутствии необходимости переводить данные в натуральный порядок после БПФ и ОБПФ для их совместной связки. В этой статье я постараюсь отразить всё тонкости реализации проекта под названием FP23FFTK, приведу реальные примеры использования готового ядра. Проект написан на языке VHDL и заточен под FPGA фирмы Xilinx последних семейств.
Введение
В цифровой обработке сигналов, без всякого сомнения, основным инструментом анализа является быстрое преобразование Фурье (БПФ). Алгоритм находит применение практически во всех областях науки и техники. Простейшим физическим примером преобразования Фурье может служить восприятие звука человеком. Всякий раз, когда мы слышим звук, ушная раковина автоматически выполняет сложное вычисление, проделать которое человек способен лишь после нескольких лет обучения математике. Суть явления заключается в том, что слуховой орган представляет звук в виде спектра последовательных значений громкости для тонов различной высоты, а превращает получаемую информацию в воспринимаемый звук.
В вопросах радиотехники алгоритмы БПФ находят применение в свёртке и при проектировании цифровых корреляторов, используется при обработке изображений, а также в аудио- и видеотехнике (эквалайзеры, спектроанализаторы, вокодеры). Кроме того методы БПФ лежат в основе всевозможных алгоритмов шифрования и сжатия данных (jpeg, mpeg4, mp3), а также при работе с длинными числами. БПФ используется в гидроакустических системах для обнаружения надводных кораблей и подводных лодок, в радиолокационных системах для получения информации о скорости, направлении полета и расстоянии до целей.
Различные модули БПФ имеются в наличии практически в любом пакете прикладных программ, предназначенных для научных исследований, например в Maple, MATLAB, GNU Octave, MathCAD, Mathematica. Специалист должен понимать процесс преобразования Фурье и уметь грамотно его применять для решения поставленных задач, где это необходимо.
Первая программная реализация алгоритма БПФ была осуществлена в начале 60-х годов XX века в вычислительном центре IBM Джоном Кули под руководством Джона Тьюки. В 1965 году ими же была опубликована статья, посвященная алгоритму быстрого преобразования Фурье. Данный метод лег в основу многих алгоритмов БПФ и получил название по фамилиям разработчиков – Cooley-Tukey. С тех пор было выпущено достаточно много различных публикаций и монографий, в которых разрабатываются и описываются различные методы и алгоритмы БПФ, снижающие количество выполняемых операций, уменьшающие энергетические затраты и ресурсы и т.д. На сегодняшний день БПФ – это название не одного, а большого ряда различных алгоритмов, предназначенных для быстрого вычисления преобразования Фурье.
Теория
Я не буду подробно рассказывать теорию из курса радиотехнического факультета типа «Цифровая обработка сигналов». Вместо этого я приведу подборку самых полезных источников, где можно познакомиться как с теоретическими изысканиями, так и с практическими выкладками и особенностями реализации тех или иных алгоритмов БПФ.
Статьи на Хабре:
- Простыми словами о преобразовании Фурье
- Практическое применение преобразования Фурье
- Преобразование Фурье в действии…
- Фурье-обработка цифровых изображений
- Matlab и быстрое преобразование Фурье
- Спектральный анализ сигналов
Книги:
- Э.С. Айфичер, Барри У. Дервис., Цифровая обработка сигналов. Практический подход
- Рабинер Л., Голд Б., Теория и применение цифровой обработки сигналов
Сайт DSPLIB:
- БПФ с прореживанием по времени
- БПФ с прореживанием по частоте
- Быстрое преобразование Фурье. Принцип построения
- Полифазное БПФ
Алгоритм
Узел БПФ выполнен по алгоритму Кьюли-Туки с основанием 2. Все вычисления для такой реализации сводятся к многократному выполнению базовой операции «бабочка». Метод преобразования – по конвейерной схеме с частотным прореживанием (для БПФ) и временным прореживанием (для ОБПФ). В алгоритме применяется схема двукратного параллелизма. Такой подход позволяет производить обработку непрерывного потока комплексных отсчетов с АЦП, частота дискретизации которого в 2 раза выше тактовой частоты обработки. То есть «бабочка» БПФ за один такт производит вычисление сразу для двух комплексных отсчетов. Если использовать 4- или 8-кратный параллелизм, то возможна обработка потока данных от АЦП или любого другого источника на частоте в 4 и 8 раз выше, чем частота обработки. Такие схемы часто применяются в задачах полифазного преобразования Фурье (Polyphase FFT) и представляют особый интерес.
Для экономии RAMB памяти в кристалле ПЛИС, начиная с определенной стадии БПФ (при NFFT > 4096 точек) применяется линейная интерполяция поворачивающих коэффициентов – разложение в ряд Тейлора до первой производной. Это позволяет вместо хранения всего набора коэффициентов использовать лишь часть из них, а остальные получать путем приближенного вычисления из исходного набора. Жертвуя ресурсами примитивов DSP48, производится экономия ресурсов блочной памяти RAMB, что для узлов БПФ является критичным местом в любой аппаратной реализации на ПЛИС. Об этом подробнее будет рассказано далее.
Структурная схема
В структуре реализованного узла БПФ можно выделить 3 функциональных узла: преобразование данных из целочисленного типа в специальный формат с плавающей точкой, входной буфер для записи отсчетов сигнала и ядро БПФ, которое содержит различные законченные узлы специального назначения.
Схематический вид синтезированного проекта: Input buffer + FP converters + FFT Core
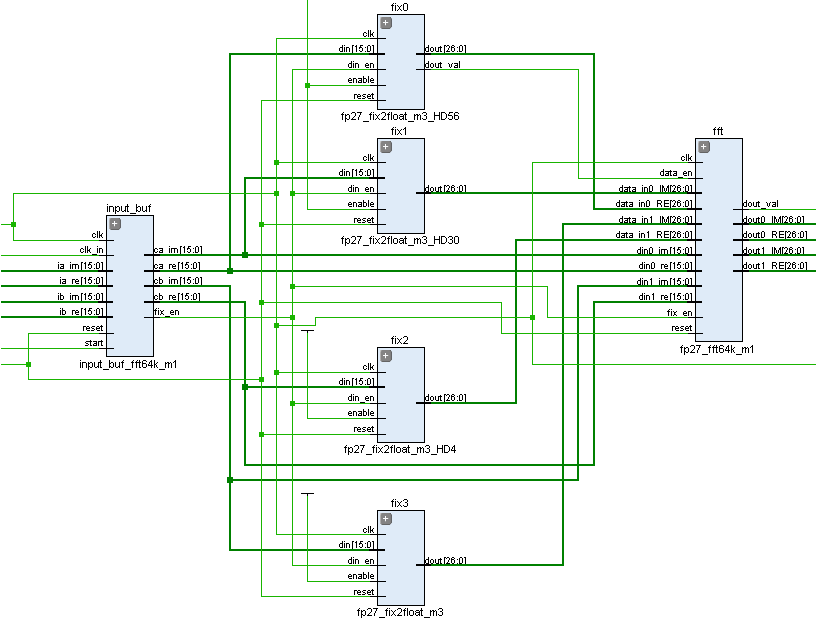
Для увеличения эффективности все вычисления проводятся в специальном 23-битном формате с плавающей запятой FP23. Это прогрессивная реализация алгоритмов FP18 и FP27, на базе которых построена вся логика. Для формата FP23 характерны следующие особенности: разрядность слова – 23 бит, мантиссы – 16, экспоненты – 6 и знака – 1. Формат FP23 специально адаптирован к архитектуре ПЛИС и учитывает внутренние особенности работы блоков кристалла, таких как универсальный блок цифровой обработки DSP48 и блоки памяти RAMB18. Применение формата с плавающей запятой обеспечивает высокую точность обработки сигналов с АЦП вне зависимости от их амплитуды и позволяет избежать вычислительной ошибки при масштабировании данных, свойственной системам с целочисленным аппаратным вычислением с ограничением по разрядности вычислений. Почитать о нём можно в моей предыдущей статье.
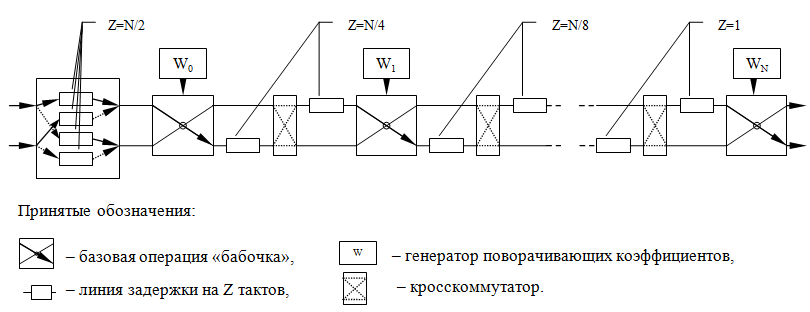
На следующем рисунке изображена конвейерная схема вычисления БПФ для последовательности длины N=2^n. Она содержит:
- Входной буфер – осуществляет первичную подготовку данных на входе БПФ (перестановка отсчетов в зависимости от реализации и используемой схемы АЦП),
- Генераторы поворачивающих коэффициентов – узлы распределенной и блочной памяти, в которых хранятся отсчеты синуса и косинуса,
- Бабочка – базовая операция ядра БПФ (с децимацией по частоте и по времени),
- Линии задержки и кросскоммутаторы — обеспечивают поступление на вход «бабочек» элементов обрабатываемого массива с нужными индексами.
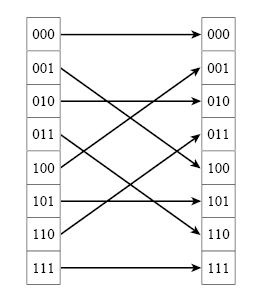
Конвейер ядра БПФ построен так, что данные на его вход должны поступать в естественном порядке, а на выходе БПФ формируется поток данных в разрядо-инверсном порядке. Для ОБПФ все наоборот – данные на входе в двоично-инверсном порядке, а на выходе в естественном или натуральном порядке. В этом состоит главное преимущество этой связки БПФ и ОБПФ по сравнению с готовыми ядрами от Xilinx, для которых данные на входе должны быть строго в натуральном порядке, а данные на выходе зависят от включенной опции.
Что такое двоично-инверсный порядок и как он получается из натурального порядка наглядно демонстрирует следующая картинка (для последовательности N = 8 отсчетов):
Входной буфер
Строится на распределенной или внутренней памяти кристалла ПЛИС. В последней реализации представляет собой память, на вход которой поступает N комплексных отсчетов, а на выходе формируется две пачки N/2 отсчетов, причем в первой пачке содержатся отсчеты [0; N/2 -1], а во второй пачке [N/2; N-1]. По сути входной буфер является нулевой линией задержки для узла БПФ и в нём происходит первичная перестановка данных.
Исходный код на VHDL для реализации памяти буфера или линий задержки достаточно прост и по сути осуществляет работу двухпортовой памяти:
PR_RAMB: process(clk) is
begin
if (clk'event and clk = '1') then
if (enb = '1') then
ram_dout <= ram(conv_integer(addrb));
end if;
if (ena = '1') then
if (wea = '1') then
ram(conv_integer(addra)) <= ram_din;
end if;
end if;
end if;
end process;
Генераторы поворачивающих коэффициентов
Для каждой стадии вычисления бабочки нужно разное количество коэффициентов. Например, для первой стадии нужен всего 1 коэффициент, для второй стадии 2, для третьей 4 и т.д. пропорционально степени двойки. В связи с этим поворачивающие коэффициенты реализуются на базе распределенной (SLICEM) и внутренней (RAMB) памяти FPGA в виде ROM-памяти, которая хранит отсчеты синуса и косинуса. Для экономного хранения используется приём, позволяющий сократить ресурсы памяти. Он заключается в том, что с помощью четверти периода синуса и косинуса можно построить весь период гармонического сигнала, используя лишь операции со знаком и направлением счета адреса памяти. При необходимости можно хранить лишь восьмую часть коэффициентов, а остальные участки получать путём переключения источника данных гармонических сигналов между собой и изменением направления счетчика. В текущей реализации это не приносит выигрыша производительности и незначительно экономит ресурс блочной памяти, причем существенно увеличивает объем занимаемых логических ресурсов кристалла.
Пример фомирования косинуса:
- Первая четверть: счетчик адреса +1, отсчеты cos,
- Вторая четверть: счетчик адреса +1, отсчеты -sin,
- Третья четверть: счетчик адреса -1, отсчеты -sin,
- Четвертая четверть: счетчик адреса -1, отсчеты cos,
Нехитрая логика на мультиплексорах счетчика адреса и данных позволяет в 4 раза сэкономить память ПЛИС.
Коэффициенты хранятся в целочисленном формате разрядностью 16 бит и уже после извлечения из памяти они переводятся в формат FP23. Мной была проведена оценка производительности для схем с целочисленным форматом и с форматом в плавающей точке. Практика показала, что первый вариант в 1.5 раза экономит память кристалла, при этом никак не ухудшается производительность всего ядра, а добавленная задержка на преобразование форматов на некоторых стадиях даже вносит некоторые преимущества (выравнивание задержек по данным и коэффициентам для бабочки с децимацией по частоте).
Хранение поворачивающих коэффициентов для малых длин БПФ осуществляется в распределенной памяти ПЛИС в ячейках SLICEM до стадии, когда необходимо хранить 512 комплексных отсчетов с суммарной разрядностью 32 бит. При больших длинах БПФ используется блочная память кристалла RAMB18, причем для хранения 1024 пар отсчетов необходимо использовать всего 2 блока RAMB18, что эквивалентно 36*1K = 16*2*1K = 18K * 2. Отметим, что 1024 коэффициента преобразуются в 2048 с помощью описанного ранее метода частичного хранения данных, а с учётом двукратного параллелизма Radix-2, это позволяет обслуживать БПФ длиной NFFT = 4096 отсчетов.
Для длин БПФ NFFT > 4096 отсчетов применяется разложение коэффициентов в ряд Тейлора до первой производной, что позволяет с достаточно высокой точностью рассчитывать поворачивающие коэффициенты и дополнительно экономить память ПЛИС. Опустим некоторые теоретические выкладки и перейдем непосредственно к практическим особенностям вычисления.
Для больших значений NFFT поворачивающие коэффициенты хранятся не напрямую в блочной памяти ПЛИС, а получаются путём расчета по методу Тейлора. Расчётные формулы для действительной и мнимой части поворачивающих коэффициентов в упрощенном виде приведены ниже:
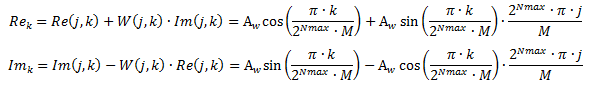
В этих формулах:
Aw – амплитуда поворачивающих коэффициентов (как правило, Aw = 216),
2Nmax – максимальное число поворачивающих коэффициентов, ограничивающее использование блочной памяти ПЛИС (в текущей реализации, 2Nmax = 2048, то есть Nmax=12),
k – счетчик всех значений коэффициентов на текущей стадии БПФ, k = 0 … 2Nmax∙M-1,
j – счетчик промежуточных значений коэффициентов на текущей стадии БПФ, j = 0 … M-1,
M – число, зависящее от стадии вычисления, определяется как M=2stage, где stage – номер стадии БПФ.
Rek, Imk – расчётные значения поворачивающих коэффициентов.
На рисунке приведена упрощенная схема реализации вычислений коэффициентов по схеме Тейлора (счетчик адреса используется для извлечения коэффициентов из памяти и математических операций с данными)
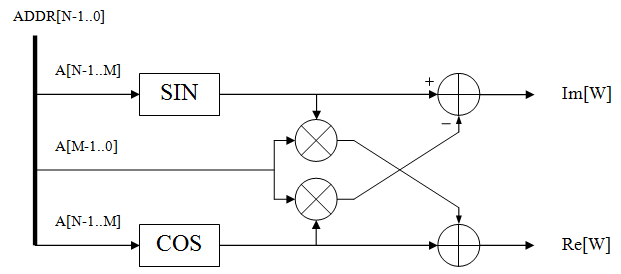
Так как вычисления поворачивающих коэффициентов производятся с помощью математических действий и извлечения данных из блочной памяти, то каждая стадия хранения коэффициентов занимает ресурсы DSP48 и RAMB18. Для представленных расчетных формул был написан алгоритм, использующий 2 операции умножения гармонических функций и 1 операцию умножения на значение счетчика, что эквивалентно 3 блокам DSP48.
Если бы в ядре не использовалась схема Тейлора, то для каждой следующей стадии ресурсы блочной памяти росли бы пропорционально степени 2. Для 4096 отсчетов затрачивается 4 примитива RAMB, для 8192 отсчетов — 8 примитивов и т.д. При использовании алгоритма Тейлора, количество примитивов блочной памяти всегда остается фиксированным и равным 2.
Код для создания коэффициентов синуса и косинуса строится на базе VHDL-функции (необходимо использовать пакет MATH). Функция синтезируема и успешно преобразует данные в 32-битный вектор данных в целочисленном формате.
function rom_twiddle(xx : integer) return std_array_32xN is
variable pi_new : real:=0.0;
variable re_int : integer:=0;
variable im_int : integer:=0;
variable sc_int : std_array_32xN;
begin
for ii in 0 to 2**(xx-1)-1 loop
pi_new := (real(ii) * MATH_PI)/(2.0**xx);
re_int := INTEGER(32768.0*COS( pi_new));
im_int := INTEGER(32768.0*SIN(-pi_new));
sc_int(ii)(31 downto 16) := STD_LOGIC_VECTOR(CONV_SIGNED(im_int, 16));
sc_int(ii)(15 downto 00) := STD_LOGIC_VECTOR(CONV_SIGNED(re_int, 16));
end loop;
return sc_int;
end rom_twiddle;Таблица ресурсов для реализации поворачивающих коэффициентов:
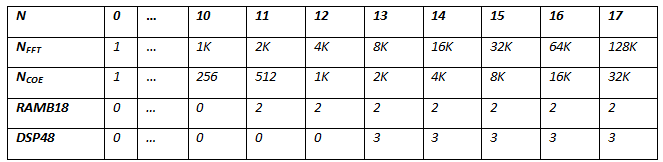
Бабочка
Каждая бабочка для БПФ и ОБПФ использует 4 умножителя и 6 сумматоров-вычитателей, реализуя функцию комплексного умножения и сложения / вычитания. Из представленных функциональных блоков только умножители используют ячейки DSP48, по 1 штуке каждый. Отсюда следует, что на одну бабочку БПФ приходится всего 4 примитива DSP48. Формулы для вычисления бабочки с прореживанием по частоте и по времени приведены в источниках выше. Реализуются бабочки достаточно просто. Ресурсов блочной памяти бабочка не занимает. Подводный камень здесь простой и легко обходится: следует учитывать задержки на вычисления в процессе расчета данных и выгрузки поворачивающих коэффиицентов Wn. Для БПФ и ОБПФ эти задержки — разные!
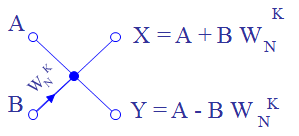
Линии задержки
Кросс-коммутаторы и линии задержки реализуют перестановку данных в требуемый порядок для каждой стадии БПФ. Самое подробное описание алоритма перестановки приведено в книге Рабинера и Голда! Используют распределенную или блочную память ПЛИС. Никаких трюков для экономии памяти здесь, к сожалению, провести нельзя. Это самый неоптимизируемый блок и реализуется как есть.
Таблица ресурсов для реализации линий задержки в общем виде:
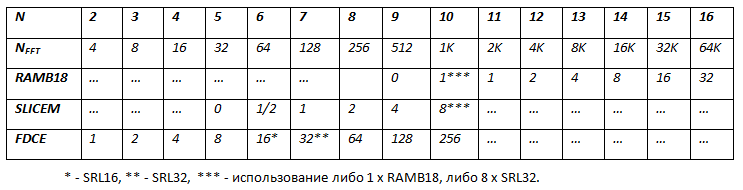
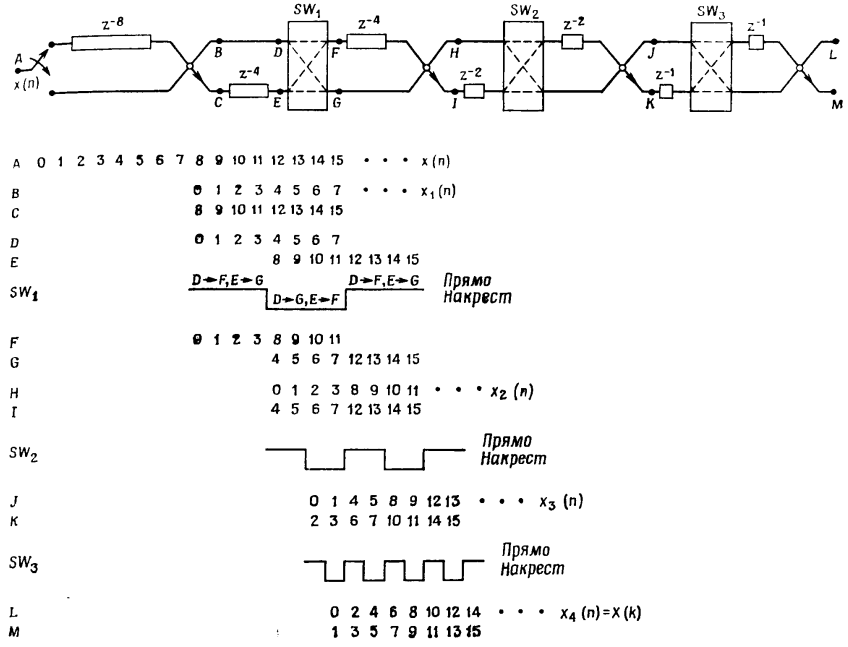
Позволю себе вытащить картинку из книги, в которой показан процесс двоичной перестановки в линиях задержки на разных стадиях для NFFT = 16.
На C++ этот алгоритм реализуется так:
for (int cnt=1; cnt<stages+1; cnt++)
{
int CNT_ii = pow(2.0,(stFFT-cnt));
int CNT_jj = pow(2.0,(cnt-1));
for (int jj=0; jj<CNT_jj; jj++)
{
for (int ii=0; ii<CNT_ii; ii++)
{
int jN = ii+jj*(N_FFT/pow(2.0,cnt-1));
int iN = N_FFT/(pow(2.0,cnt));
int xx = jj*N_FFT/pow(2.0,cnt); // mix data
// -------- A, B, WW, IND[A], IND[B], IND[W] -------- //
ButterflyFP(Ax, Bx, CFW, jN, jN+iN, ii*CNT_jj);
}
}
}На бабочку поступают отсчеты A и B с номерами jN и jN+iN, а коэффициенты WW поступают с номерами ii*CNT_jj. Для полного понимания процесса достаточно взглянуть на схему двоичной перестановки и пример из книги.
Общий объем ресурсов
Дальнейшие действия достаточно просты — все узлы необходимо правильно соединить между собой, учесть задержки на выполнение различных операций (математика в бабочках, выгрузка коэффициентов для разных стадий). Если все сделать правильно, в конечном результате у вас получится готовое рабочее ядро.
В следующей таблице представлен расчет ресурсов для ядра БПФ FP23FFTK и для ядра БПФ от Xilinx (опции Floating point, Radix-2, Pipelined Streaming I/O). В таблице для ядра Xilinx приведены две колонки ресурсов для блочной памяти: (1) — без преобразования порядка из двоично-инверсного в натуральный (bitreverse output data) и (2) — с преобразованием (natural output data).
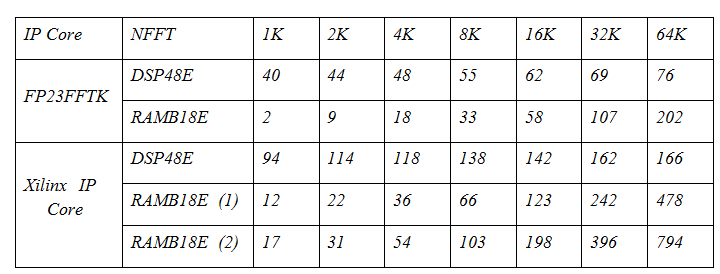
Как видно из таблицы, ядро FP23FFTK занимает в 2.5 раза меньше примитивов DSP48 при NFFT = 64K, что обусловлено в первую очередь форматом данных с урезанной мантиссой и экспонентой (FP23 vs FP32). Кроме того, ядро занимает в 2.5 раза меньше компонентов блочной памяти для опции bitreverse и в 4 раза меньше для опции natural в ядре Xilinx. Обосновать это можно усеченным форматом данных, но он дает выигрыш лишь в 1.5 раза. Остальные улучшения связаны с особенностями хранения поворачивающих коэффициентов и использованием алгоритма Тейлора.
Пример: ядро БПФ от Xilinx обязано принимать данные на входе в натуральном порядке (особенность ядра!), поэтому для связки БПФ + ОБПФ ядер Xilinx при NFFT = 64K потребуется ~1600 ячеек блочной памяти, а для той же связки в формате FP23FFTK всего лишь ~400 ячеек RAMB, поскольку для ОБПФ не требуется переводить данные в естественноую форму, а на его выходе данные уже в натуральном порядке. Эта особенность позволяет строить компактные фильтры сжатия (связка БПФ+ОБПФ) на быстрых свертках в небольших кристаллах ПЛИС без потери производительности!
Ниже приведен лог синтеза ядра БПФ для NFFT = 65536 точек:
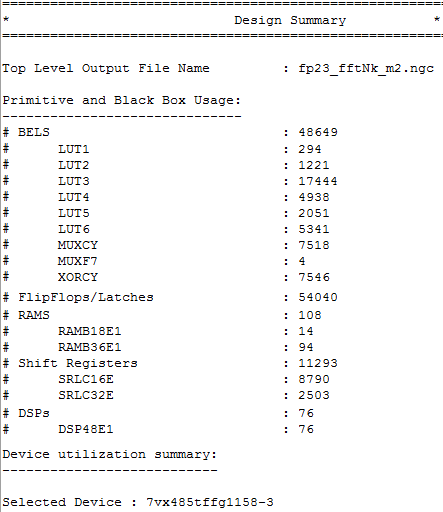
Примеры реализации на ПЛИС
1. 4 канала прямого БПФ. ПЛИС: Virtex-6 SX315T (~1300 RAMB, ~1400 DSP48). 4x FP23FFTK, NFFT = 16K
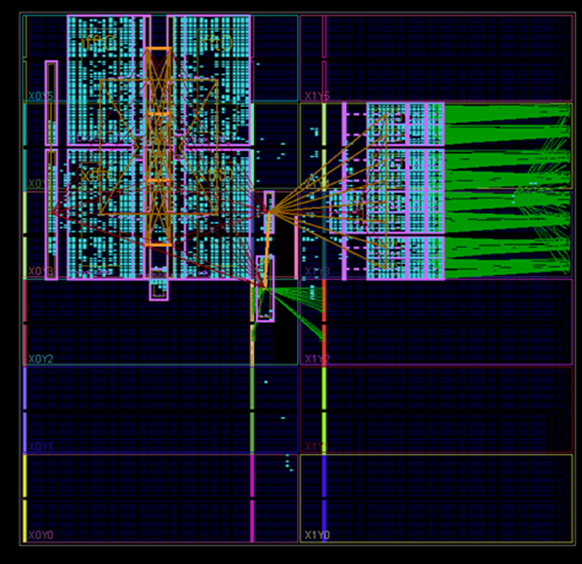

3. БПФ + ОБПФ 64К (большой фильтр сжатия). ПЛИС: XC7VX1140TFLG-2 (~3700 RAMB, ~3600 DSP48).
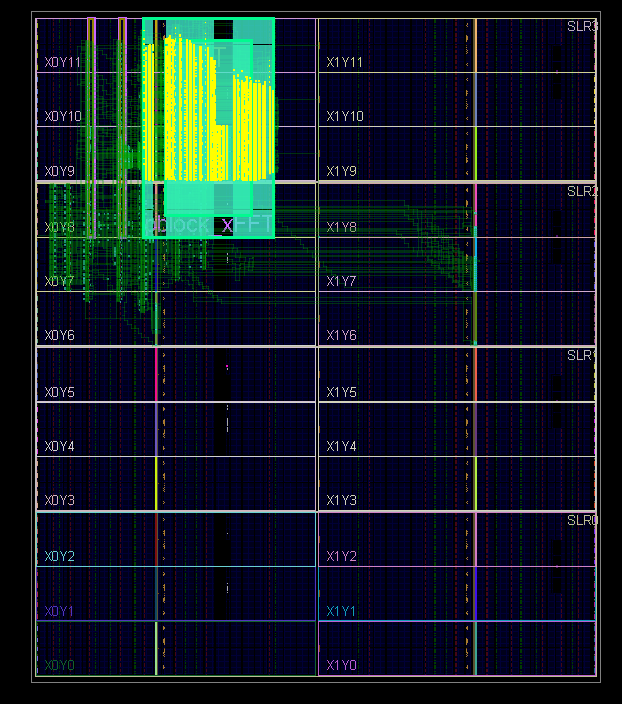
4. Рисунок случайной разводки БПФ (напоминает бабочку):
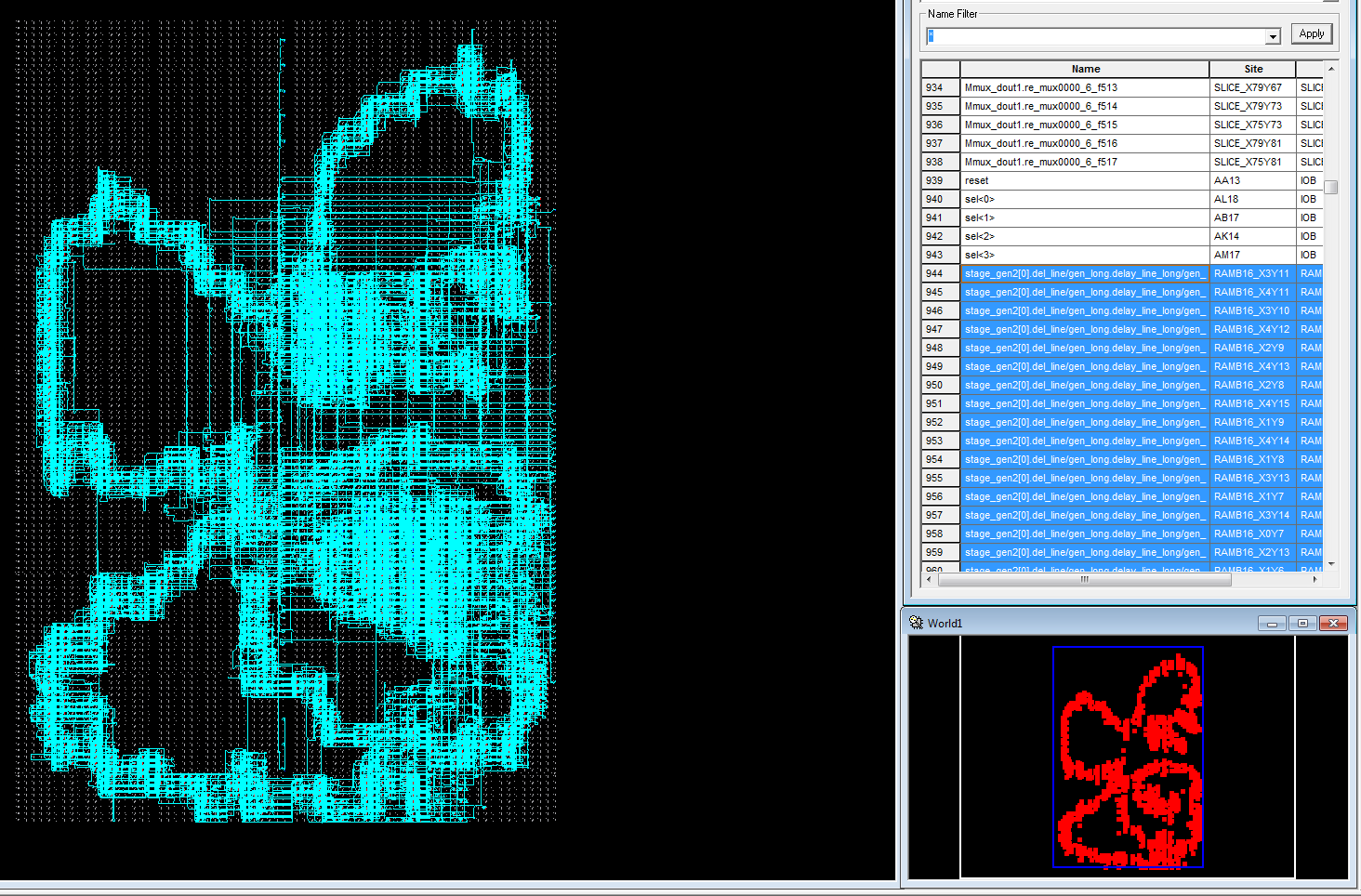
Проверка ядра
Для моделирования и отладки ядра БПФ в формате с плавающей точкой на ПЛИС применялись разные средства разработки.
А) Тестирование RTL-модели ядра БПФ проводилось с помощью САПР Xilinx Vivado и Aldec Active-HDL. Несмотря на высокую производительность Vivado, она имеет несколько недостатков, один из которых – плохие средства редактирования кода. Вроде бы продукт постоянно развивается, но некоторые полезные примочки до сих пор отсутствуют в программе, поэтому исходный код написан в Notepad++, настроенный под работу с VHDL/Verilog файлами. В отличие от Vivado, Active-HDL моделирует намного быстрее, а также позволяет сохранять временные диаграммы после выхода из приложения. Modelsim в работе не применялся за неимением лицензии :)
Б) Тестирование программной модели ядра БПФ было проведено в Microsoft Visual Studio, для чего на языке C++ было написано приложение, повторяющее RTL-модель, но без задержек и тактовых частот, что позволило достаточно быстро и эффективно отлаживаться на разных стадиях проектирования (генераторы поворачивающих коэффициентов, перестановочные коммутационные узлы, математические операции, реализация алгоритма Тейлора и полное законченное ядро БПФ).
В) Полное тестирование проводилось в Matlab / GNU Octave. Для отладки были созданы скрипты с различными тестовыми сигналами, но идеальным для визуального моделирования оказался простейший ЛЧМ-сигнал с различными настройками девиации, амплитуды, смещения и других параметров. Он позволяет проверить работу БПФ на всем участке спектра, в отличие от гармонических сигналов. При тестировании синусоидальными сигналами, я несколько раз попадал в ловушку, которую устраняет применение ЛЧМ-сигнала. Если подать синусоидальный сигнал определенной частоты на вход БПФ, то на выходе я получал хорошую гармонику на нужной частоте, но стоило мне изменить период входной синусоиды – возникали ошибки. Природу этих ошибок в процессе отладки RTL-кода отследить было непросто, но затем я нашёл ответ: неправильные задержки в узлах бабочек и поворачивающих коэффициентов на некоторых стадиях вычислений. Использование ЛЧМ-сигнала устранило эту проблему и позволило подобрать правильные задержки на каждой стадии вычисления БПФ. Также с помощью m-скриптов проводилось сравнение работы C++ и RTL-моделей, а также проверялась разница в вычислениях в формате с плавающей точкой FP23 и в формате float/double.
Алгоритм тестирования
Этот процесс может показаться несколько рутинным, но именно в такой последовательности мне удалось добиться правильности работы всех узлов БПФ. Возможно, он поможет и вам, если вы будете пользоваться ядром в своих проектах.
1. Запустить скрипт Matlab / Octave для создания эталонного сигнала. Вы можете управлять следующими переменными:
- NFFT – длина БПФ/ОБПФ, количество точек преобразования,
- Asig – амплитуда входного сигнала (0-32767),
- Fsig – частота входного сигнала,
- F0 – начальная частота ЛЧМ (фаза сигнала),
- Fm – частота огибающей ЛЧМ сигнала (для непрямоугольной огибающей),
В результате создается два файла (для действительной и мнимой компоненты), которые используются в C++ и RTL-моделях.
2. Создать проект в Microsoft Visual Studio, взяв исходные коды на C++ в соответствующем каталоге.
3. Собрать и запустить проект. Вы можете задавать следующие переменные в h-файле:
- NFFT – длина БПФ/ОБПФ (зависит от выбора в п.1),
- SCALE – масштабирующий фактор, определяющий диапазон чисел после преобразования данных из формата FP23 в формат INT16. Диапазон значений от 0 до 0x3F.
- _TAY (0/1) – использование расчёта коэффициентов по алгоритму Тейлора (для NFFT > 4096).
4. Создать HDL-проект в среде Vivado или Active-HDL, взяв исходные файлы на VHDL.
5. Запустить моделирование с помощью файла из каталога testbench. Вы можете задать следующие опции в этом файле:
- NFFT – длина БПФ/ОБПФ (зависит от выбора в п.1),
- SCALE – масштабирующий фактор, определяющий диапазон чисел после преобразования данных из формата FP23 в формат INT16. Диапазон значений от 0 до 0x3F.
- USE_SCALE (TRUE/FALSE) – использование расчёта коэффициентов по алгоритму Тейлора или расчёт коэффициентов напрямую (для NFFT > 4096). Обратная величина для переменной _TAY из п.3.
- USE_FLY_FFT (TRUE/FALSE) – использование бабочек в ядре БПФ. В целях отладки опция осталась, практической пользы не несет.
- USE_FLY_IFFT (TRUE/FALSE) – использование бабочек в ядре ОБПФ.
6. Повторно запустить m-скрипт (из п.1) для проверки работы C++ / RTL-ядер БПФ и ОБПФ.
После проведения этих магических действий на экране отразятся графики входного сигнала, и графики прохождения сигнала через узлы БПФ и ОБПФ. Для тестирования только одного узла БПФ необходимо взять другой m-скрипт из каталога math и сделать некоторые изменения в исходных файлах.
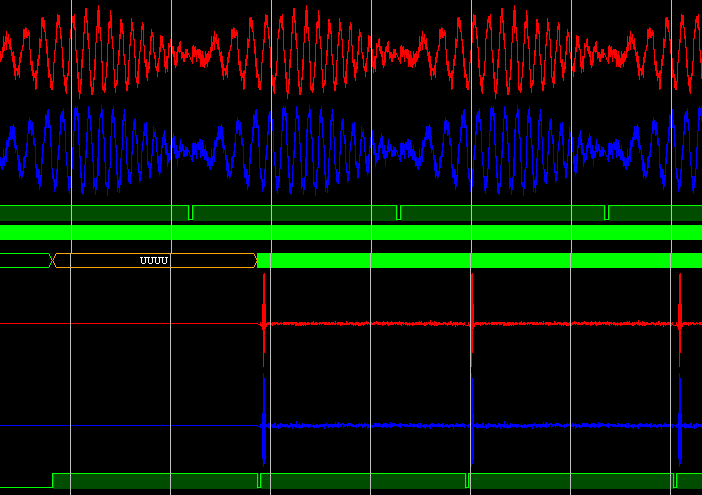
Визуальная проверка C++ и RTL-модели (связка БПФ + ОБПФ):
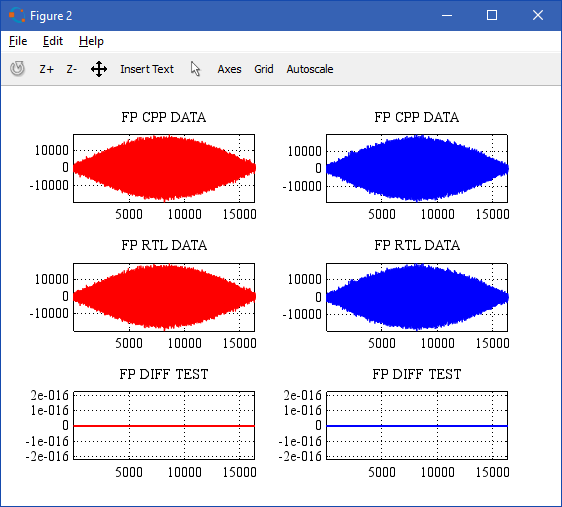
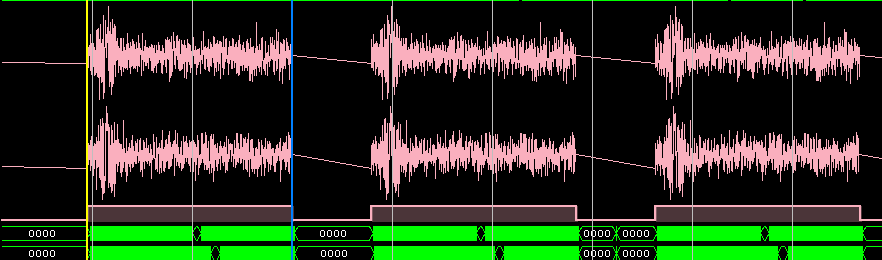
БПФ входного сигнала:
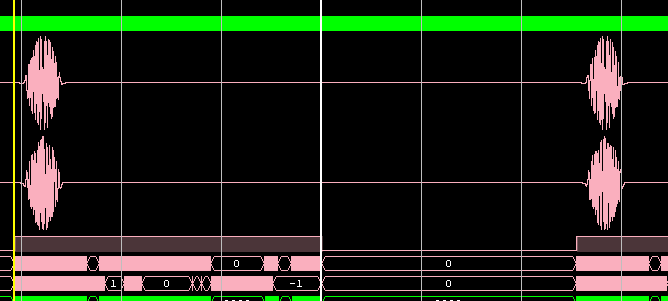
Еще один пример тестирования (входной сигнал и результат БПФ):
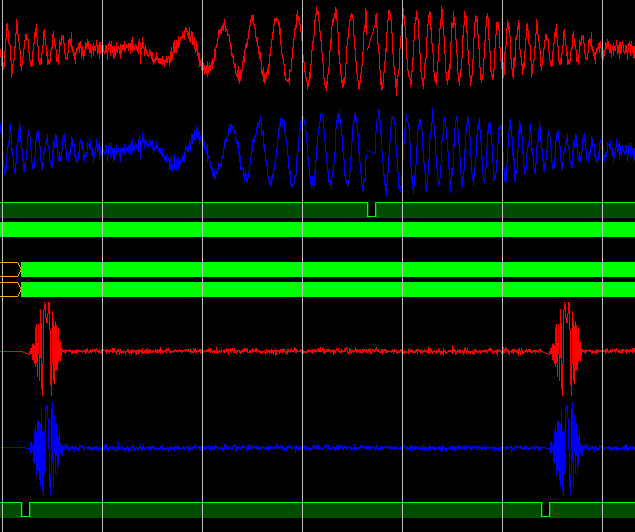
Тестирование в железе (отладка в ChipScope) на ПЛИС Kintex-7:
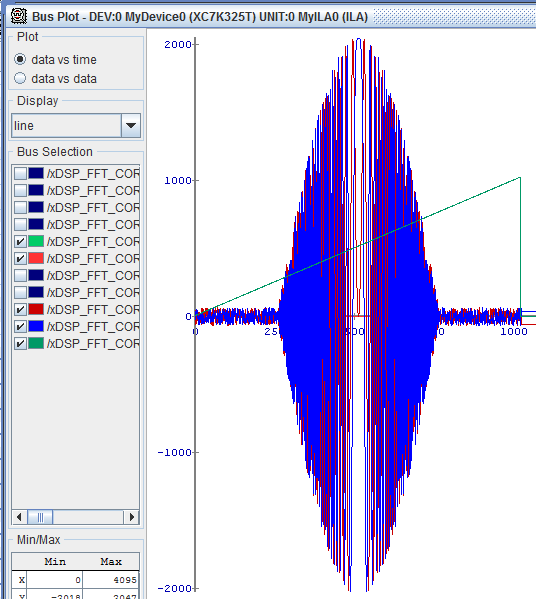
Работа фильтра — сжатый ЛЧМ-импульс (в исходных кодах реализации фильтра сжатия нет):
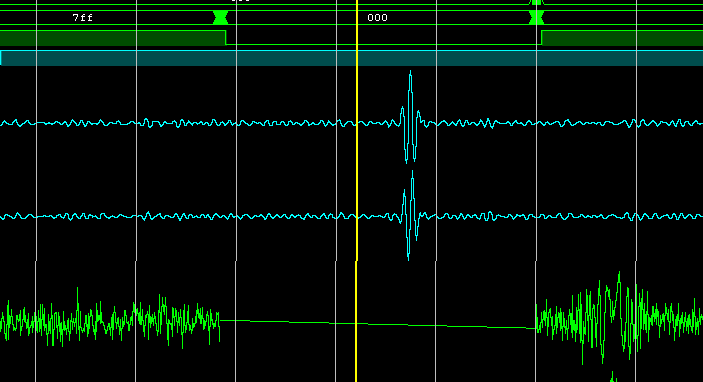
Особенности ядра БПФ FP23FFTK
- Реализация на уровне вентилей и примитивов Xilinx.
- Язык описания – VHDL.
- Длина преобразования NFFT = 8-256K точек.
- Гибкая настройка длины преобразования NFFT.
- Специализированный формат чисел в плавающей точке FP23, (разрядность мантиссы – 16 бит).
- Масштабирование выходных данных при переводе в формат с фиксированной точкой.
- Компактное хранение поворачивающих коэффициентов через разложение в ряд Тейлора до первой производной.
- Хранение четверти периода коэффициентов в распределенной и блочной памяти.
- Бабочка для БПФ – децимация по времени, для ОБПФ – по частоте.
- БПФ: данные на входе – в прямом порядке, на выходе в двоично-инверсном.
- ОБПФ: данные на входе в двоично-инверсном порядке, на выходе – в прямом.
- Конвейерная схема обработки с двухкратным параллелизмом. Radix-2
- Минимальная длина пачки данных равна NFFT отсчетов в непрерывном или блочном режиме.
- Высокая скорость вычислений и небольшой объем занимаемых ресурсов.
- Реализация на последних кристаллах ПЛИС (Virtex-6, 7-Series, Ultrascale)
- Отсутствие необходимости затратной операции bitreverse для связки БПФ+ОБПФ
- Открытый исходный код.
Исходный код
Все исходники ядра БПФ FP23FFTK на VHDL (включая базовые операции в формате FP23), модель для проверки на С++ и m-скрипты для Matlab / Octave доступны в моем профиле на гитхабе.
Дальнейшие планы
Разумеется, развитие проекта на этом не заканчивается. В моих планах на базе уже созданных моделей сделать много интересного и нового, например:
- Для увеличения точности вычислений при больших длинах БПФ реализовать формат FP32 (аналогичный IEEE-754) с учетом особенностей ПЛИС, длина мантиссы — 25 бит.
- Узлы БПФ и ОБПФ в формате FP32, длина NFFT = 256K и выше на примере фильтра сжатия.
- Полифазные БПФ по схеме Radix-4, Radix-8, что позволит в конвейерном режиме обрабатывать потоки данных от АЦП на очень высоких частотах.
- Схема Ultra-long FFT (на базе 2D-FFT) с применением внешней памяти для NFFT = 1M-256M точек.
Переписать исходники на SystemVerilog. Надо ли?
Заключение
На получение стабильного результата в железе и полную реализацию этого проекта я потратил несколько лет (чистое время не считал, увы). Проект создавался урывками, вечерами, выходными, периодически забрасывался и частично или полностью менялся подход к различным узлам. Часто некоторые идеи отбрасывали назад или сильно забрасывали вперед, причем иногда чисто случайно. Один из главных вывод, который я сделал в процессе этой работы — необходимость тщательной проверки каждой стадии проектирования независимыми средствами. Например, без модели на С++ мне иногда вообще не удавалось продвинуться в реализации, поэтому пришлось написать множество небольших тестов и отлаживать каждый кусок отдельно перед общим тестированием узла.
Надеюсь, это ядро кому-то поможет в задачах ЦОС и найдет применение в ваших проектах. Некоторые моменты я деликатно опустил и не стал делать на них акцент (расчет интегральной ошибки преобразования, шумы квантования в формате FP23 и т.д.). Выражаю благодарность dsmv2014, который всегда приветствовал мои идеи и положительно воспринимал мои авантюрные начинания по реализации тех или иных задач цифровой обработки сигналов на ПЛИС.
Спасибо за внимание!
Автор: capitanov





