Урок Maxima
Введение
Maxima — свободная система компьютерный алгебры (Computer algebra system — CAS), основанная на Commmon Lisp. В своих функциональных возможностях она едва уступает другим современным платным CAS, таким как Mathcad, Mathematica, Maple; может проводить аналитические (символьные) вычисления, численные расчеты, строить графики (при помощи gnuplot). Имеется возможность написания скриптов и даже трансляции их в код на Common Lisp с последующей компиляцией. В виду того, что maxima писалась из разрабатывалась программистами lisp, ее синтаксис может показаться несколько запутанным, поскольку язык является сразу и императивным и функциональным. Я попытаюсь разъяснить именно эти моменты и доступно изложить суть функционального подхода, и совсем не буду акцентировать внимания на конкретных математических функциях: их довольно легко освоить самостоятельно. В данной статье рассматривается именно особенности исчисления и синтаксических конструкций maxima.
Оболочки
Разумеется, вызывать интерпретатор maxima из консоли не очень удобно. Мы хотим смотреть на красивые формулы, которые отрендерены с помощью latex. Поэтому, для начинающих, я бы посоветовал поставить оболочку wxMaxima. Если вы увлекаетесь TeXmacs — можете настроить и его в качестве оболочки (если честно, я не пробовал). Ну и для любителей emacs есть imaxima, для работы в буфере. Ставится он буквально из коробки.
Знакомство
На первый взгляд все просто: вводим выражение, заканчивающееся точкой с запятой, получаем ответ. Можете испробовать maxima в качестве калькулятора, вычислить сумму двух чисел, подсчитать синус угла и т.п. Копнем глубже, что же происходит.
Атомы
Символы, числа и логические константы true и false представляют собой простейшие объекты системы. Из них выстраиваются все остальные выражения и структуры языка, поэтому их называют атомарными (неделимыми) или просто атомами.
Переменные

В системе различают свободные и означенные переменные. Означенные переменные — связанные переменные, переменные к которым приписано какое то значение. При интерпретации имя переменной заменяется на ее значение. Задать переменную можно с помощью знака ":". Свободные переменные не связаны не с каким значением и мы можем оперировать с ними абстрактно, например, складывать два символьных выражения.
Контекст вычисления
При вычислении каждой команды формируется ее вычислительный контекст. Он представляет собой совокупность связей между именами переменных и их значениями, а так же некоторые параметры интерпретации. Различают два вычислительных контекста: локальный и глобальный. Глобальный контекст — общий для всех интерпретируемых команд, определяет текущее состояние интерпретатора. Локальный контекст создается на время выполнения одной команды, и действителен только для нее. Наиболее приоритетными являются связи и параметры локального контекста.

Здесь значение переменной a берется из глобального контекста, а для локального устанавливается опция развертывания произведений, т.е. дальше произведения не будут развертываться сами по себе.
Блокировка вычислений

Попробуем сложить две переменные. А теперь поставим перед ними символ одинарной ковычки. Это оператор блокировки вычислений. Если мы поставим его перед именем переменной — в результате получим имя этой переменной, перед вызовом функции — символьное выражение вызова функции. Зачем? Иногда вам может потребоваться с помощью одной функции обработать выражение другой функции и на выходе получить функцию или число, например вычисление неопределенного интеграла. Другими словами вы имеете возможность представлять выражение как данные и манипулировать с ним. Однако если вы попробуете остановить вычисление суммы двух чисел, то вычисления не прекратятся. Это связано с тем, что оператор одинарной кавычки не останавливает простейшего упрощения выражения (простые операции над числами, сокращение дробей). Так же вычисления не остановятся, если вы попытаетесь посчитать значение функции рационального (float) аргумента.
И так, система Maxima не различает функции алгоритмические и функции математические, в ней они являются одним языковым элементом. В терминологии самого интерпретатора, операторы которые могут быть вычислены называются verb, те операторы, которые так остаются в невычесленом виде называются noun. Для инициирования вычисления всех noun необходимо в контексте вычислений выставить опцию nouns.

Вычисления
Мы узнали, что интерпретатор различает понятия символьного выражения и его вычисления. В каких случаях происходит вычисление? Самый очевидный случай — когда мы пытаемся посчитать какое то выражение (2+3, например). Ввели выражение — получили его значение. Посчитали функцию от аргумента — получили значение. Ввели имя переменной — получили ее значение. Мы узнали, что значением у переменной может быть как атом, так и символьное выражение. Когда еще происходит вычисление? Вычисление происходит при присваивание переменной значения. Значение стоящее справа от двоеточия вычисляется перед присвоением, поэтому при присвоении переменной символьного выражения мы ставим кавычку, что бы остановить это вычисление. Есть особенный вид присвоения (оператор два двоеточия), когда вычисляется как выражение справа, так и выражение слева. Так же перед вычислением функции вычисляются все ее аргументы.

Результатом вычисления переменной a слева оказывается переменная b.
Пример
Рассмотрим простой пример — построение множества всех подмножеств. Как оказалось, Maxima имеет встроенные типы для работы с множествами, а такой функции, увы, нет. Напишем ее.
Для начала разберемся что есть множества. По видимому, множества в Maxima основаны на другой структуре данных — односвязных списках. Что такое список понимают все. Они имеют три основные функции для работы с ними: получение элемента в голове списка (first), получение списка состоящего из исходного без первого элемента (rest), добавление нового элемента в начало (cons) и объединение двух списков (append). Аналогичные функции имеются и в любой реализации lisp, но чаще всего, называются немного по другому: car, cdr, cons, append соответственно.
Как вы обычно представляли себе алгоритм для решения такой задачи? Можно было бы представить подмножества в виде характеристического вектора и перебрать их все. Однако покажем именно функциональный подход. Нетрудно заметить, что каждый элемент входит ровно в половину подмножеств. Этого простого факта уже достаточно для того, что бы построить рекурсивный алгоритм. Выкинем один элемент a из множества A. Множество всех подмножеств A будет состоять из объединения множества всех подмножеств Aa и множества всех подмножества Aa, где к каждому элементу добавлено a. С помощью последнего утверждения можно сколько угодно рекурсивно понижать размерность задачи, сведя ее к тривиальному случаю. Для реализации нам необходима дополнительная функция от двух параметров (элемента и множества множеств), которая добавляла бы указанный элемент в каждое множество.

Обратим внимание, что объявление функции происходит почти как и в математике. Следует обратить внимание, что при определении правая часть после знака равно не вычисляется. (Для того что бы определить функцию так, что бы ее определение вычислялось необходимо использовать форму define). Здесь появляется новая вычислительная форма if. Она работает так же как и в императивных языках. При выполнении условия вычисляется выражение после then, при невыполнении — после else. Теперь запишем искомую функцию.
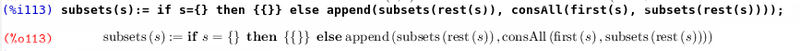
Попробуем что нибудь посчитать.
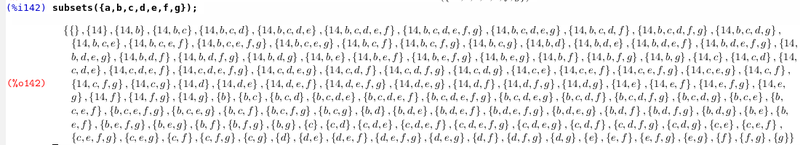
Конец
Ну вот и все. В следующей статье было бы неплохо описать реализацию наискорейшего градиентного спуска.
Автор: IVaigult





