Что такое робастный контроллер и зачем нам усложнять себе жизнь? Чем нас не устраивает стандартный, всеми узнаваемый, ПИД-регулятор?
Ответ кроется в самом названии, с англ. «robustness» — The quality of being strong and not easy to break (Свойство быть сильным и сложно сломать). В случае с контролером это означает, что он должен быть «жестким», неподатливым к изменениям объекта управления. Например: в мат. модели DC мотора есть 3 основных параметра: сопротивление и индуктивность обмотки, и постоянные Кт Ке, которые равны между собой. Для расчета классического ПИД регулятора, смотрят в даташит, берут те 3 параметра и рассчитывают коэффициенты ПИД, вроде все просто, что еще нужно. Но мотор — это реальная система, в которой эти 3 коэффициента не постоянные, например в следствии высокочастотной динамики, которую сложно описать или потребуется высокий порядок системы. Например: Rдаташит=1 Ом, а на самом деле R находиться в интервале [0.9,1.1] Ом. Так во показатели качества в случае с ПИД регулятором могут выходить за заданные, а робастный контроллер учитывает неопределенности и способен удержать показатели качества замкнутой системы в нужном интервале.
На этом этапе возникает логические вопрос: А как найти этот интервал? Находится он с помощью параметрической идентификации модели. На Хабре недавно описали метод МНК («Параметрическая идентификация линейной динамической системы»), однако дает одно значение идентифицируемого параметра, как в даташите. Для нахождения интервала значений мы использовали «Sparse Semidefinite Programming Relaxation of Polynomial Optimization Problems» дополнение для матлаба. Если будет интересно, могу написать отдельную статью как пользоваться данным пакетом и как произвести идентификацию.
Надеюсь, сейчас стало хоть не много понятнее зачем робастное управление нужно.
Не буду особо вдаваться в теорию, потому что я ее не очень понял; я покажу этапы, которые необходимо пройти, чтобы получить контроллер. Кому интересно, можно почитать «Essentials Of Robust Control, Kemin Zhou, John C. Doyle, Prentice Hall» или документацию Matlab.
Мы будем пользоваться следующей схемой системы управления:
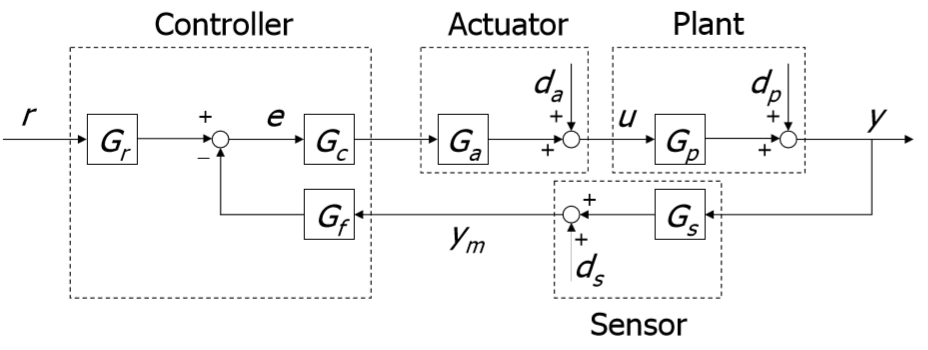
Рис 1: Блок схема системы управления
Думаю, здесь все понятно (di – возмущения).
Постановка задачи:
Найти: Gc(s) и Gf(s) которые удовлетворяют все заданные условия.
Дано: 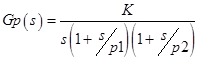 – обьект управления c неопределенностями, которые заданы интервалами:
– обьект управления c неопределенностями, которые заданы интервалами: 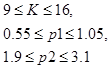
Для дальнейших расчетов будем использовать номинальные значения, а неопределенности учтем дальше.
Kn=(16+9)/2=12.5,p1n=0.8,p2n=2.5, соответственно получил номинальный объект управления:
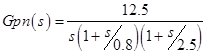
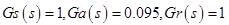
Типы возмущений:
-
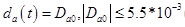 — ступенчатое возмущения усилителя с амплитудой D_a0
— ступенчатое возмущения усилителя с амплитудой D_a0 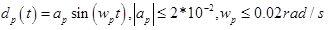 — синусоидальное возмущения обьекта управления с амплитудой a_p и частотой w_p
— синусоидальное возмущения обьекта управления с амплитудой a_p и частотой w_p-
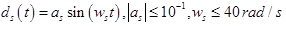 — синусоидальное возмущения сенсора с амплитудой a_s и частотой w_s
— синусоидальное возмущения сенсора с амплитудой a_s и частотой w_s
Или другими словами это характеристики шума элементов системы.
- Коэффициент усиления системы управления Kd=1
- Установившееся ошибка при входном воздействии Ramp R0=1:
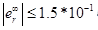
- Установившееся ошибка в присутствии da:
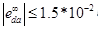
- Установившееся ошибка в присутствии dp:
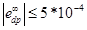
- Установившееся ошибка в присутствии ds:
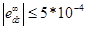
- Перерегулирование
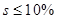
- Время регулирования
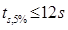
- Время нарастания
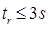
Решение
Очень детально расписывать не буду, только основные моменты.
Одним из ключевых шагов в H∞ методе это определение входных и выходных весовых функций. Эти весовые функции используются для нормирования входа и выхода и отражения временных и частотных зависимостей входных возмущений и рабочих характеристик выходных переменных (ошибок) [1]. Честно говоря, мне это практически ни о чем не говорит, особенно если впервые сталкиваешься с данным методом. В двух словах, весовые функции используются для задания нужный свойств системы управления. Например, в обратной связи стоит сенсор, который имеет шум, обычно высокочастотный, так вот, весовая функция будет своего рода границей, которую контролер не должен пересекать, что бы отфильтровать шум сенсора.
Ниже будем выводить эти весовые функции на основе рабочих характеристик.
-
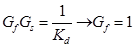 Здесь все просто
Здесь все просто - В этом пункте нам нужно определить сколько полюсов в нуле необходимо иметь для контролера (обозначим µ) чтобы удовлетворить Условие 2. Для этого воспользуемся таблицей:
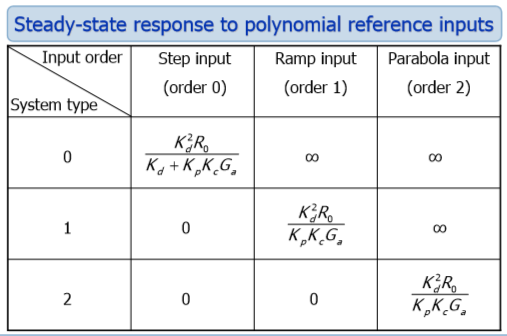
Рис 2: Ошибки по положению, скорости и ускоренияSystem type или астатизм (p) – обозначает количество полюсов в нуле, объекта управления, в нашем случае p=1 (система с астатизмом первого порядка). Так как наш объект управления и есть система с астатизмом 1 порядка, в таком случае полюсов в нуле у контроллера быть не должно. Воспользуемся формулой:
μ+p=h
Где h – порядок входного сигнала, для ramp h=1;
μ=h-p=1-1=0
Теперь воспользуемся теоремой конечных значений, чтобы найти e_r∞
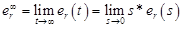
Где e_r – ошибка слежения,
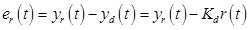
yr – действительный выход (см. Рис 1), уd – желаемый выход
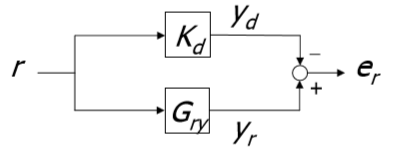
Рис 3: Определение ошибки слеженияВ итоге получим такое:
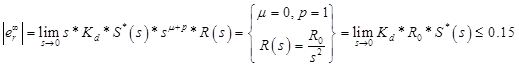
Это формула установившейся ошибки, неизвестная в данном уравнении S (Sensitivity function)
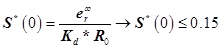
Где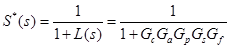 – sensitivity function, L(s) – loop function. Без понятия как они переводятся на русский, оставлю английские названия. Также complementary sensitivity function
– sensitivity function, L(s) – loop function. Без понятия как они переводятся на русский, оставлю английские названия. Также complementary sensitivity function 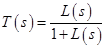 (как видно из формул, в состав S и T входят Gc – рассчитываемый контроллер, соответственно границы для S и T мы найдем из ошибок и рабочих характеристик, весовые функции определим из S и T, а матлаб из весовых функций найдёт желаемый контроллер.)
(как видно из формул, в состав S и T входят Gc – рассчитываемый контроллер, соответственно границы для S и T мы найдем из ошибок и рабочих характеристик, весовые функции определим из S и T, а матлаб из весовых функций найдёт желаемый контроллер.)
В двух словах об S и T [1].- Sensitivity function, S(s), описывает выход y(s) как функцию возмущения da и dp, также связывает ошибку слежения и входное воздействие (для низких частот)
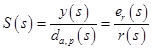
- Complementary sensitivity function, T(s), связывает выход системы с входным воздействием, а также показывает на сколько шум сенсора ds влияет на выход системы (для высоких частот).
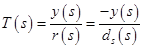
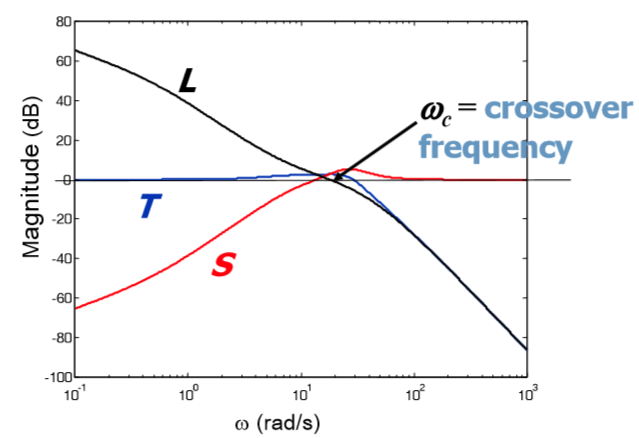
Рис 4: Диаграмма Боде для S,T и LИз графика видно что S ослабляем низкочастотные возмущения, в то время как Т ослабляет высокочастотные возмущения.
- Sensitivity function, S(s), описывает выход y(s) как функцию возмущения da и dp, также связывает ошибку слежения и входное воздействие (для низких частот)
- Воспользуемся теоремой конечных значений для e_da
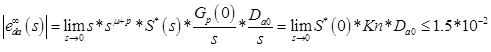
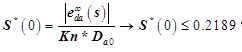
Так как у нас получилось два неравенства найдем условие удовлетворяющее обоих:
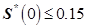
Это условие говорит, где Sensitivity function должна пересекать 0 dB axis на диаграмме Боде.
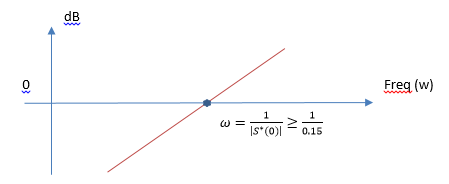
Рис 5: Боде для S - Dp у нас гармоническое возмущение, низкочастотное. Создадим маску для S в районе частот wp
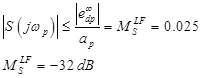
Это значение показывает что S должен находиться ниже -32 dB для частот wp, что бы отфильровать возмущения
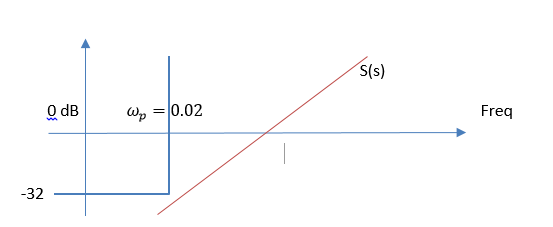
Рис 6: Маска для S - Ds также гармоническое возмущение высоких частот, здесь свою роль будет выполнять T
Выполним тоже самое:
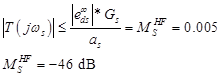
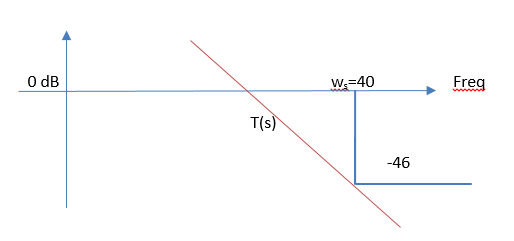
Рис 7: Маска для ТКомплексный порядок весовых функций определяется из условии маски и частоты пересечения с 0 осью. В нашем случаи от wp до w примерно одна декада, а так как у нас есть -32 dB то S должен быть минимум 2 порядка. Тоже самое касается и Т.
В итоге схематически ограничение имеют следующий вид для S и Т соответственно:
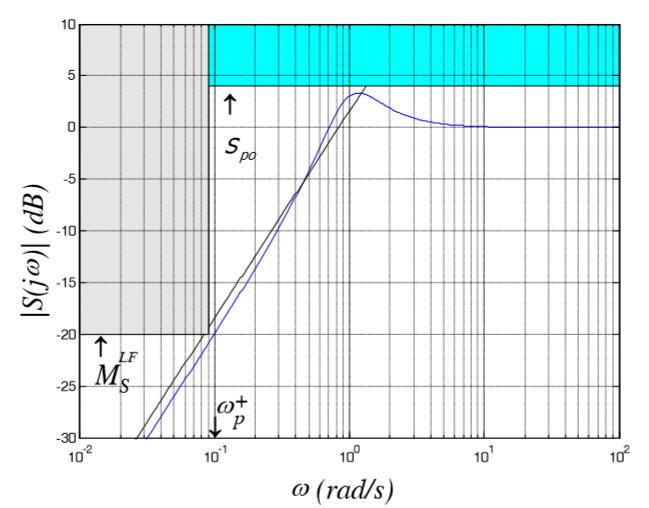
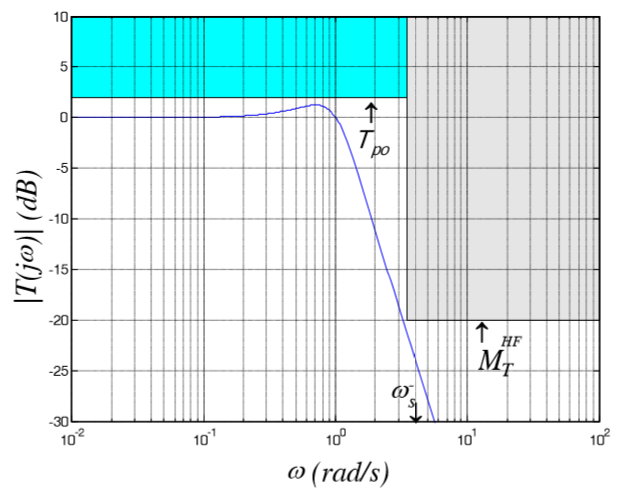
Рис 8: Все маски для S и T - Для перевода временных характеристик воспользуемся графиками
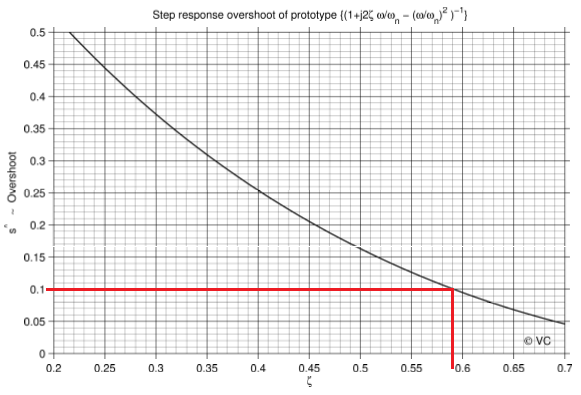
Рис 9: График зависимости коеффициента демпфирования от переригулированияЗная переригулирование найдем коеффициент демфирования для 10% ->
ξ=0.59
Зная коеффициент демфирования найдем (резонансное) максимально допустимое значение для S и T
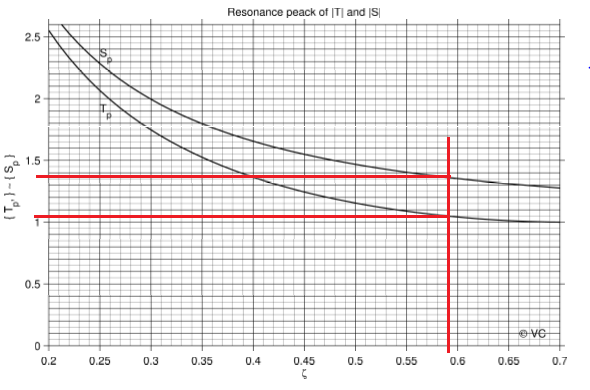
Рис 10: График зависимости S_p0 и T_p0 от коеффициента демфированияS_p0=1.35
T_p0=1.05 - Из времени регулирования и настраивания найдем насколько быстрая должна быть система управления
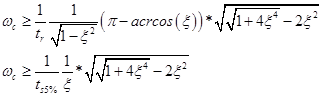
Далее найдем натуральную частоту для S
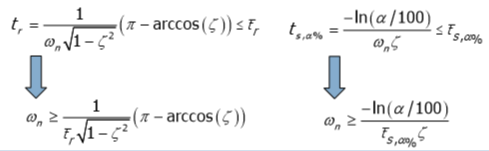
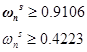
Натуральная частота для T находим по диаграмме Боде. По условию 5 в частоте 40 rad/s T должен находиться ниже -46 dB, а значит при наклоне в -40 dB/дек натуральная частота должна находиться ниже 4 rad/s. Строя Боде, подбираем оптимальное значение, я получил что:
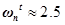
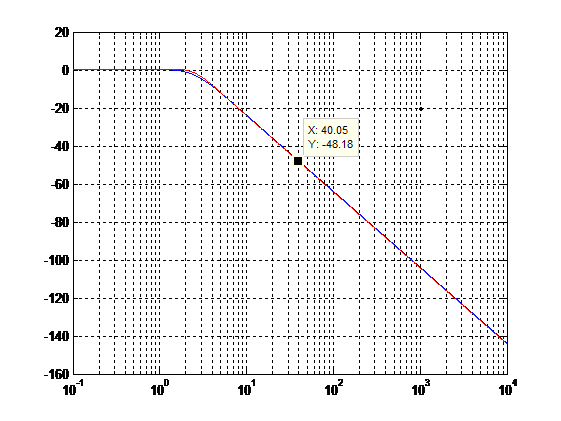
Рис 11: Боде T-функцииПосле этого у нас есть все данные для построения S T, которые потом трансформируем в весовых функций. S T имеют следующую форму:
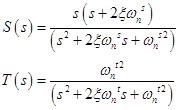
Обычно для построения весовых функций используют Butterworth коэффициенты
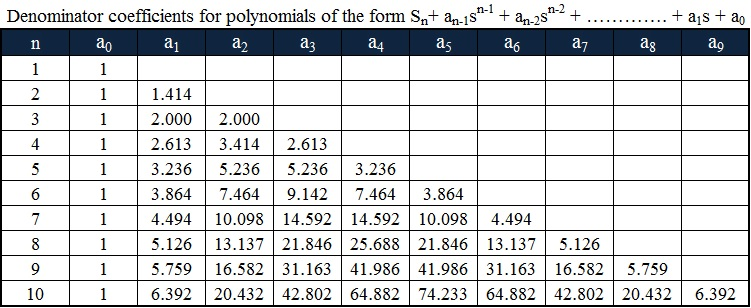
Весовые функции имеют вид:
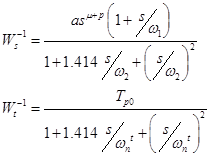
Для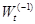 все просто, и нас есть все необходимое, что бы подставить в формулу. Для
все просто, и нас есть все необходимое, что бы подставить в формулу. Для 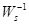 нужно еще несколько расчетов.
нужно еще несколько расчетов.
Так как рабочие характеристики дают нам граничные условия в рамках которых наш контроллер будет выполнять все условия. Весовые функции объединяют в себе все условия и потом используются как правая и левая граница в которых находиться контроллер удовлетворяющий все условия.
Для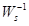
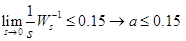 этот параметр называют generalized DC gain, он отображает поведения для низких частот (s=0)
этот параметр называют generalized DC gain, он отображает поведения для низких частот (s=0)
-
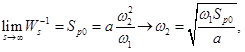 , w1 выбираем примерно возле частоты возмущения или на одну декаду ниже (поставим в 0,0005 rad/s)
, w1 выбираем примерно возле частоты возмущения или на одну декаду ниже (поставим в 0,0005 rad/s)
- • LMI solver не воспринимает нули функции(zero in origine), поэтому s заменим на нуль возле начала координат (s+0.0005)
В итоге получим:
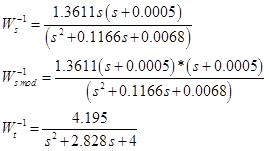
Generalized plant
Hinf метод или метод минимизации бесконечной нормы Hinfinity относится к общей формулировке проблемы управления которая основывается на следующей схеме представления системы управления с обратной связью:
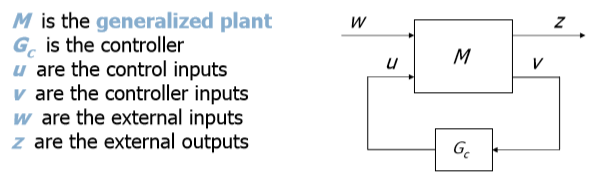
Рис 12: Обобщенный схема системы управления
Перейдем к пункту расчета контроллера и что для этого нужно. Изучение алгоритмов расчета нам не объясняли, говорили: «делайте вот так и все получиться», но принцип вполне логичен. Контроллер получается в ходе решения оптимизационной задачи:
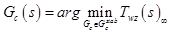
 – замкнутая передаточная функция от W к Z.
– замкнутая передаточная функция от W к Z.
Сейчас нам нужно составить generalized plant (пунктирный прямоугольник рис ниже). Gpn мы уже определили, это номинальный объект управления. Gc — контроллер который мы получим в итоге. W1 = Ws(s), W2 = max (WT(s),Wu(s)) – это весовые функции определенные ранее. Wu(s) – это весовая функция неопределенности, давайте ее определим.
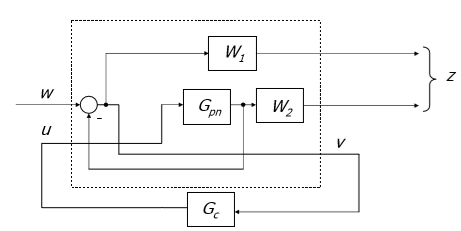
Рис 13: Раскрытая схемы управления
Wu(s)
Предположим что имеем мультипликативные неопределенности в объекте управления, можно изобразить так:
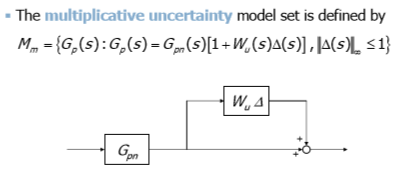
Рис 14: Мультипликативная неопределенность
И так для нахождения Wu воспользуемся матлаб. Нам нужно построить Bode все возможных отклонений от номинального объекта управления, и потом построить передаточную функцию которая опишет все эти неопределенности:
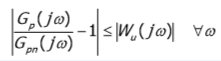
Сделаем примерно по 4 прохода для каждого параметра и построим bode. В итоге получим такое:
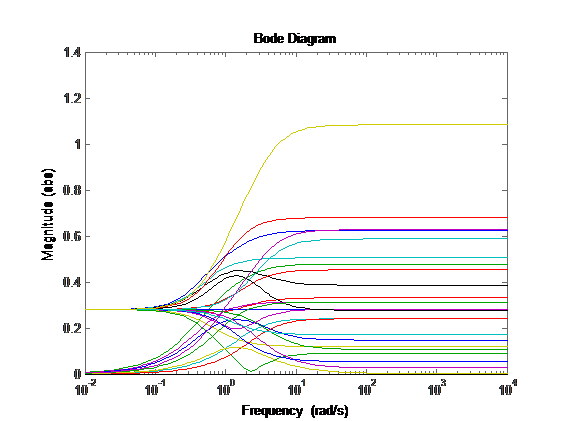
Рис 15: Диграмма Боде неопределенностей
Wu будет лежать выше этих линий. В матлаб есть tool который позволяем мышкой указать точки и по этим точкам строит передаточную функцию.
magg = vpck(mf(:,2),mf(:,1));
Wa = fitmag(magg);
[A,B,C,D]=unpck(Wa);
[Z,P,K]=ss2zp(A,B,C,D);
Wu = zpk(Z,P,K)
После введения точек старится кривая и предлагается ввести степень передаточной функции, введем степень 2.
Вот что получилось:
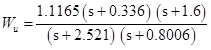
Теперь определим W2, для этого построим Wt и Wu:
Из графика видно что Wt больше Wu значит W2 = Wt.
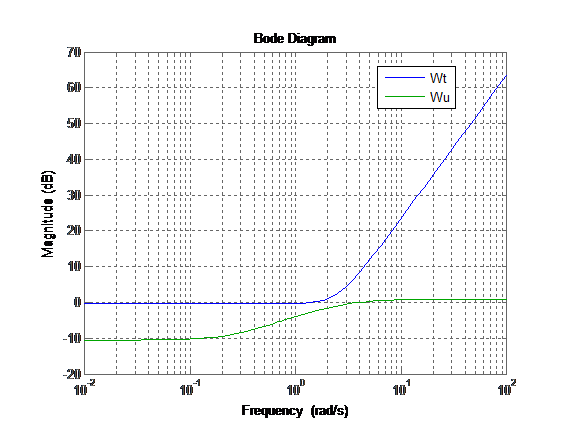
Рис 16: Опредиление W2
Дальше нам нужно в симулинке построить generalized plant как сделано ниже:
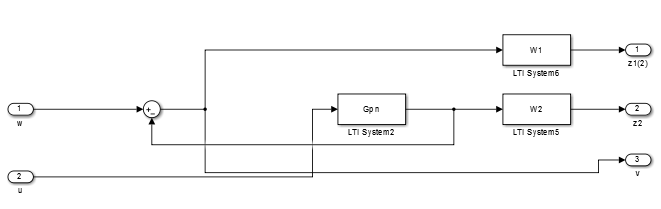
Рис 17: Блок схема Generalized plant в simulink
И сохранить под именем, например g_plant.mdl
Один важный момент:
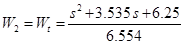 — not proper tf, если мы ее оставим так то нам выдаст ошибку. По этому заменяем на
— not proper tf, если мы ее оставим так то нам выдаст ошибку. По этому заменяем на 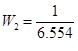 и потом добавим два нуля к выходу z2 с помощью “sderiv“.
и потом добавим два нуля к выходу z2 с помощью “sderiv“.
[Am,Bm,Cm,Dm] = linmod('g_plant');
M = ltisys(Am,Bm,Cm,Dm);
M = sderiv(M,2,[1/p 1]);
M = sderiv(M,2,[1/p 1]);
[gopt,Gcmod] = hinflmi(M,[1 1],0,0.01,[0,0,0]);
[Ac,Bc,Cc,Dc] = ltiss(Gcmod);
[Gc_z,Gc_p,Gc_k] = ss2zp(Ac,Bc,Cc,Dc);
Gc_op = zpk(Gc_z,Gc_p,Gc_k)
После выполнения этого кода получаем контроллер:
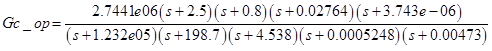
В принципе можно так и оставить, но обычно удаляют низко- и высокочастотные нули и полюсы. Таким образом мы уменьшаем порядок контроллера. И получаем следующий контроллер:
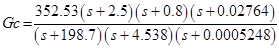
получим вот такой Hichols chart:
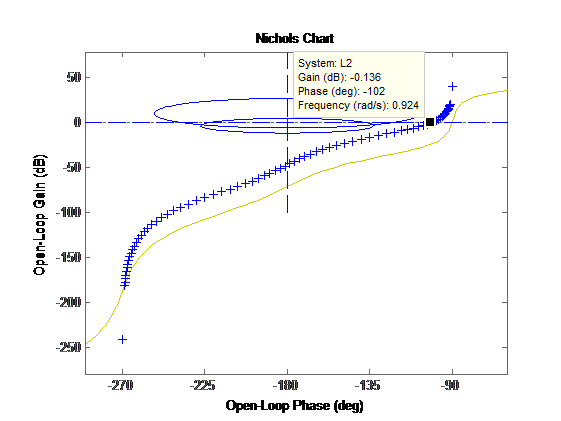
Рис 18: Hichols chart разомкнутой системы с полученным контроллером
И Step response:
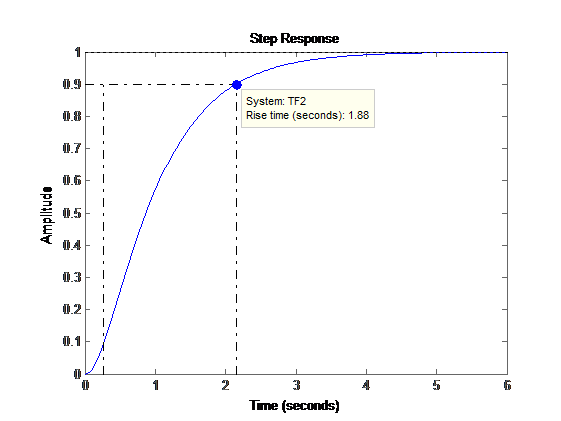
Рис 19: Переходная характеристика замкнутой системы с контроллером
А теперь самое сладкое. Получился ли наш контроллер робастным или нет. Для этого эксперимента просто нужно изменить наш объект управления (коэффициенты к, р1, р2) и посмотреть step response и интересующими характеристиками, в нашем случае это перерегулирование, время регулирования для 5 % и время нарастания [2].
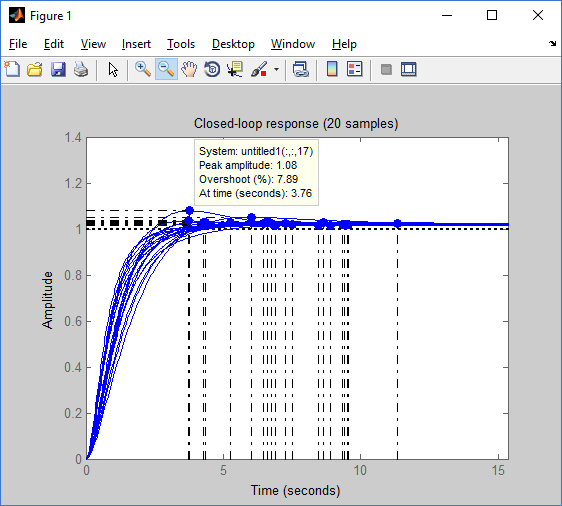
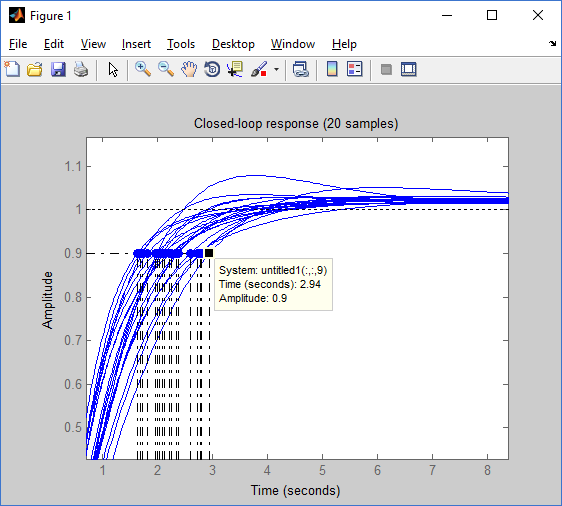
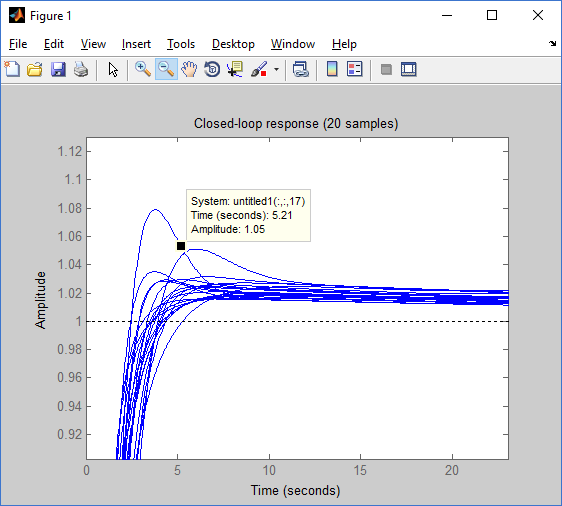
Рис 20: Временные характеристики для разных параметров объект управления
Построив 20 разных переходных характеристик, я выделил максимальные значения для каждой временной характеристики:
• Максимальное переригулирование – 7.89 %
• Макс время нарастания – 2.94 сек
• Макс время регелирования 5% — 5.21 сек
И о чудо, характеристики там где нужно не только для номинального обьекта, но и для интервала параметров.
А сейчас сравним с классичиским ПИД контролером, и посмотрим стоила игра свеч или нет.
ПИД расчитал pidtool для номинального обьекта управления (см выше):
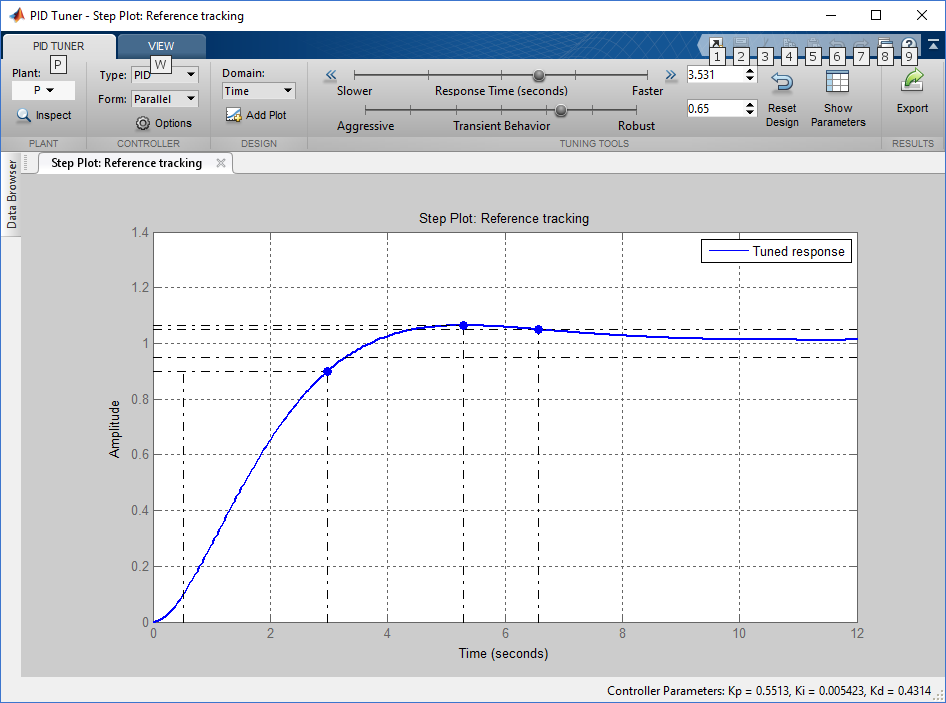
Рис 21: Pidtool
Получим такой контроллер:
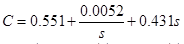
Теперь H-infinity vs PID:
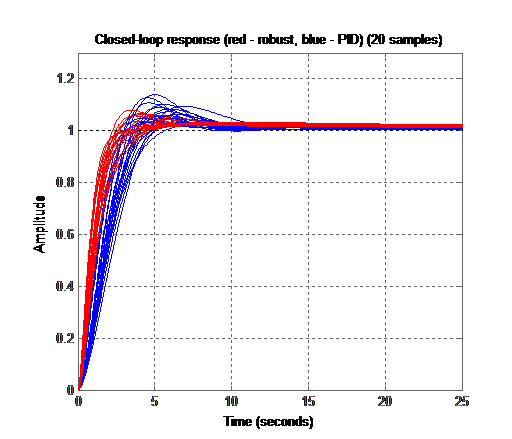
Рис 22: H-infinity vs PID
Видно что ПИД не справляется с такими неопределенностями и ПХ выходит за заданные ограничения, в то время как робастные контроллер «жестко» держат систему в заданных интервалах перерегулирования, времени нарастания и регулирования.
Что бы не удлинять статью и не утомлять читателя, опущу проверку характеристики 2-5 (ошибки), скажу, что в случае робастного контроллера все ошибки находятся ниже заданных, также был проведен тест с другими параметрами объекта:
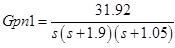
Ошибки находились ниже заданных, что означает, что данный контроллер полностью справляется с поставленной задачей. В то время как ПИД не справился только с пунктом 4 (ошибка dp).
На этом все по расчету контроллера. Критикуйте, спрашивайте.
Ссылка на файл матлаб: drive.google.com/open?id=0B2bwDQSqccAZTWFhN3kxcy1SY0E
Список литературы
1. Guidelines for the Selection of Weighting Functions for H-Infinity Control
2. it.mathworks.com/help/robust/examples/robustness-of-servo-controller-for-dc-motor.html
Автор: lggswep