По роду своей деятельности мне приходится осуществлять контроль различных параметров наземных импульсно-фазовых радионавигационных систем (ИФРНС) «Чайка» и Loran-C. В этой статье я хочу поделиться одним из методов обнаружения времени прихода импульса ИФРНС при наличии шумов. Метод применим во многих задачах поиска сигнала известной формы.
Системы относятся к классу гиперболических систем и основаны на измерении разности времени прихода радиоимпульсов, принимаемых от цепочки передающих станций. В каждой цепочке одна из станций является ведущей, а остальные – ведомые. Все они точно синхронизируются.
Основной проблемой при детектировании сигналов ИФРНС является искажение формы принимаемых радиоимпульсов за счет наложения на поверхностную волну отраженных составляющих. Составляющие сигнала, которые не распространяются вдоль поверхности, проходят различные пути за различное время. Невозможно надежно предсказать время их прихода. Однако, очевидно, что отраженные составляющие сигнала распространяются медленнее поверхностной составляющей. Они также влияют на форму принимаемого сигнала. Форма принимаемого радиоимпульса может изменяться в зависимости от времени года, времени суток, а также от погодных условий и географической местности. Для выполнения задач навигации необходим алгоритм выделения начала поверхностной составляющей радиоимпульса.
Принимаемый сигнал xt (t) во временной области может быть представлен следующим уравнением:
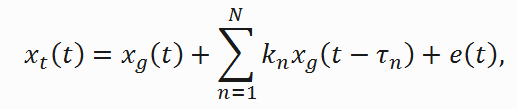 (1)
(1)
где xg (t) – поверхностная составляющая, амплитуда и задержка n-ной отраженной составляющей определяются коэффициентами kn и tn, а e (t) — шумовая компонента.
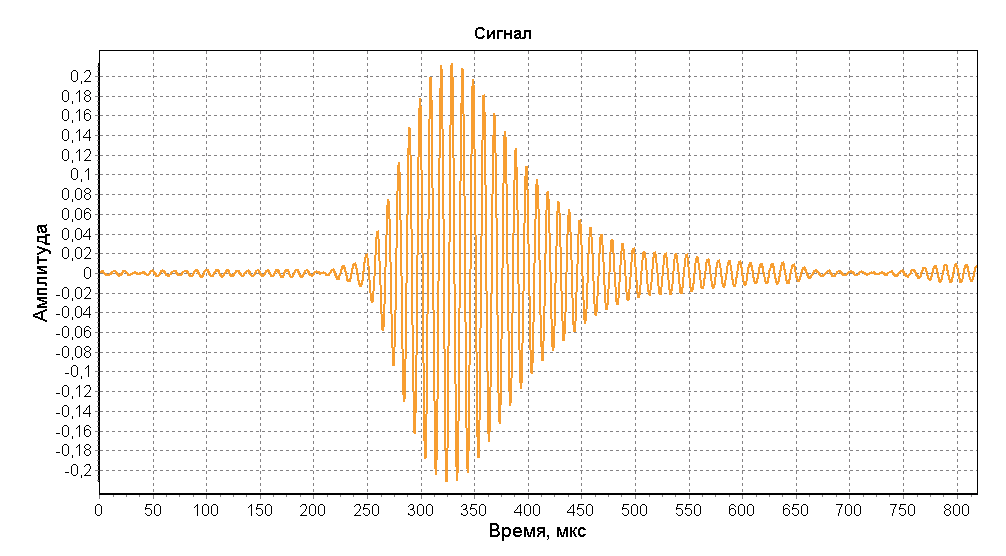
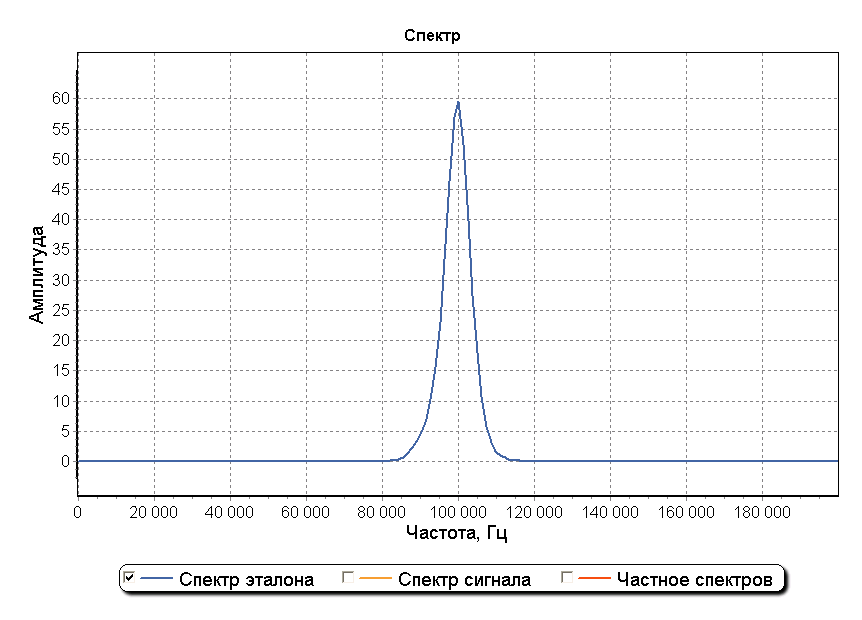
Ниже изображены эталонный импульс ИФРНС и его спектр после прохождения полосового фильтра приемника. Частота дискретизации составляет 5 МГц.
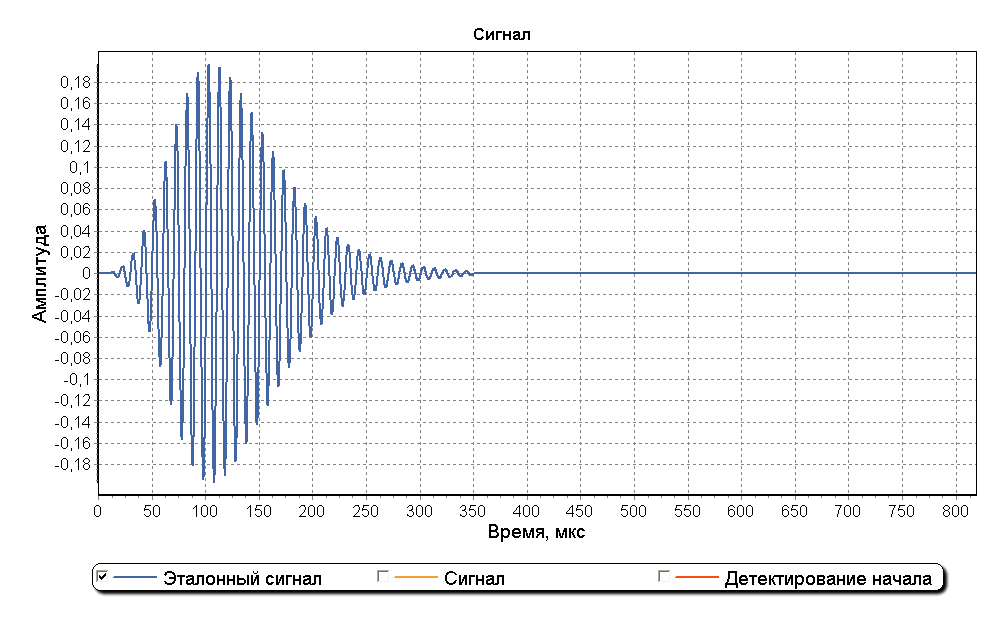
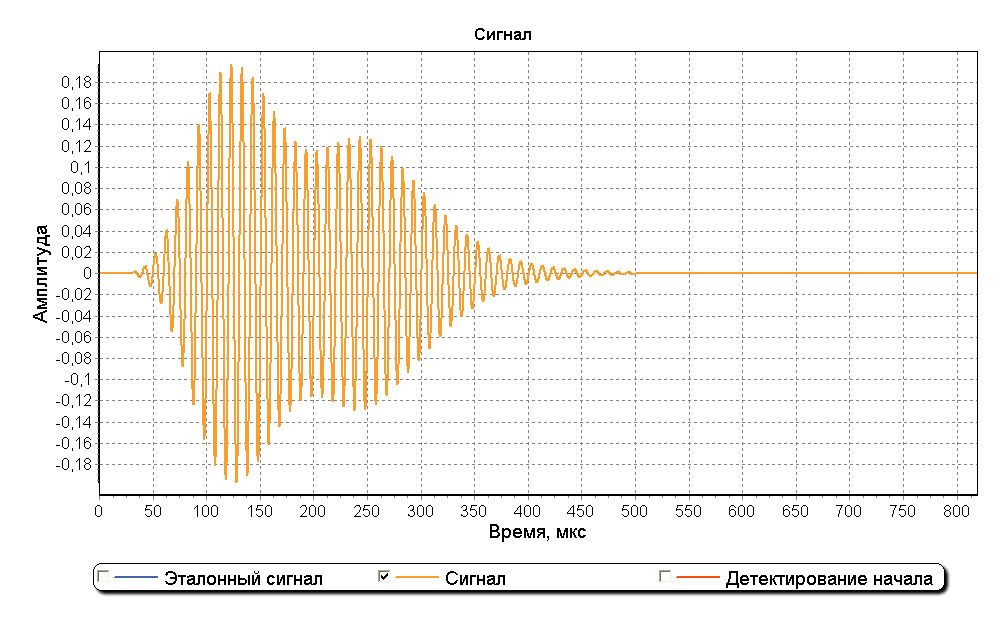
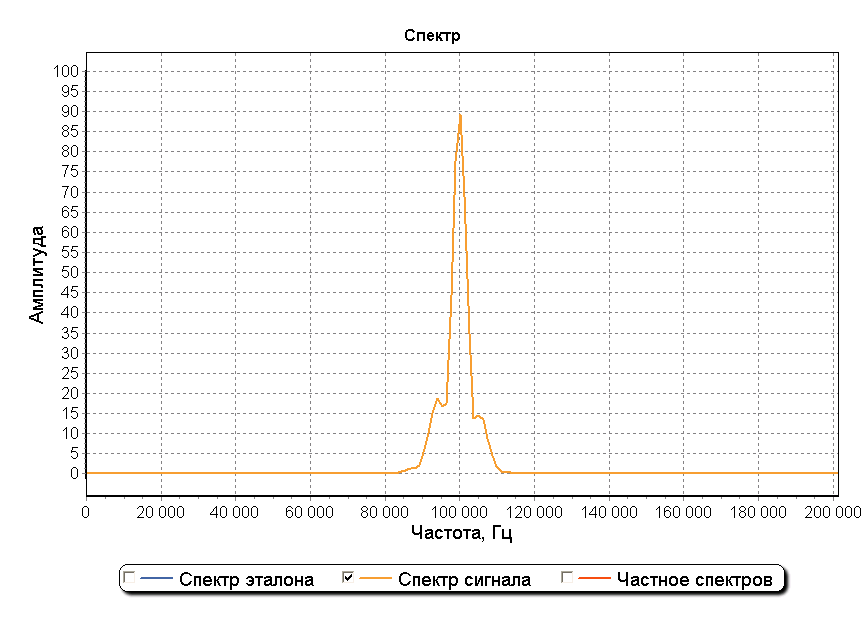
В качестве примера рассмотрим смоделированный радиоимпульс, состоящий из поверхностной и отраженной составляющих. На рисунках ниже представлены графики, на котором изображена модель импульса, состоящая из двух составляющих смещенных друг от друга на 130 мкс. Амплитуда отраженной составляющей в 2 раза ниже амплитуды поверхностной составляющей.
Эквивалентное представление сигнала в частотной области описывается как:
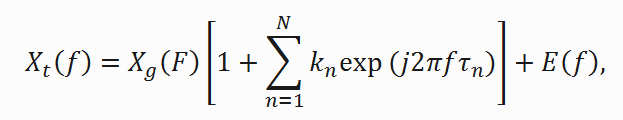 (2)
(2)
где Xt (f), Xg (F) и E (f) — спектры сигналов xt (t), xg (t) и e (t).
Примем, что спектр эталонного нормированного сигнала системы «Лоран-С» или «Чайка» обозначается как X0 (f).
Очевидно, что
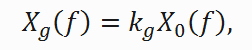 (3)
(3)
где kg — амплитуда поверхностной составляющей. Если выражение для Xg (f) из формулы (3) подставить в формулу (2) и разделить почленно все слагаемые на X0 (f), получится выражение
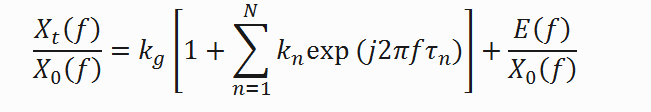 (4)
(4)
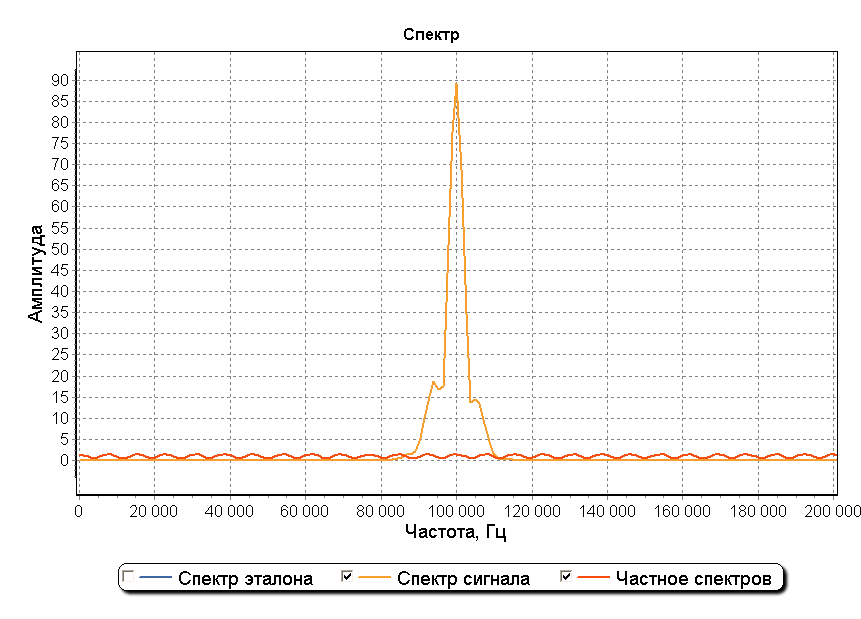
На рисунке ниже изображен график результата деления спектра сигнала на спектр эталона. Изображенный красным, график представляет собой горизонтальную пилообразную линию во всей области частот.
Обратное преобразование Фурье над выражением (4) дает формулу
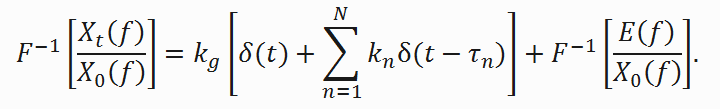 (5)
(5)
Математический смысл выражения (5) заключается в том, что во временной области мы получаем пики в виде дельта-функций в моменты появления как поверхностной, так и всех отраженных составляющих сигнала, нормированные по амплитуде.
На рисунке ниже изображен график детектирования начала составляющих сигнала. Как видно из графика отношение амплитуд составляющих сигнала равно двум и расстояние между пиками составляет 130 мкс, что соответствует параметрам построенной модели.
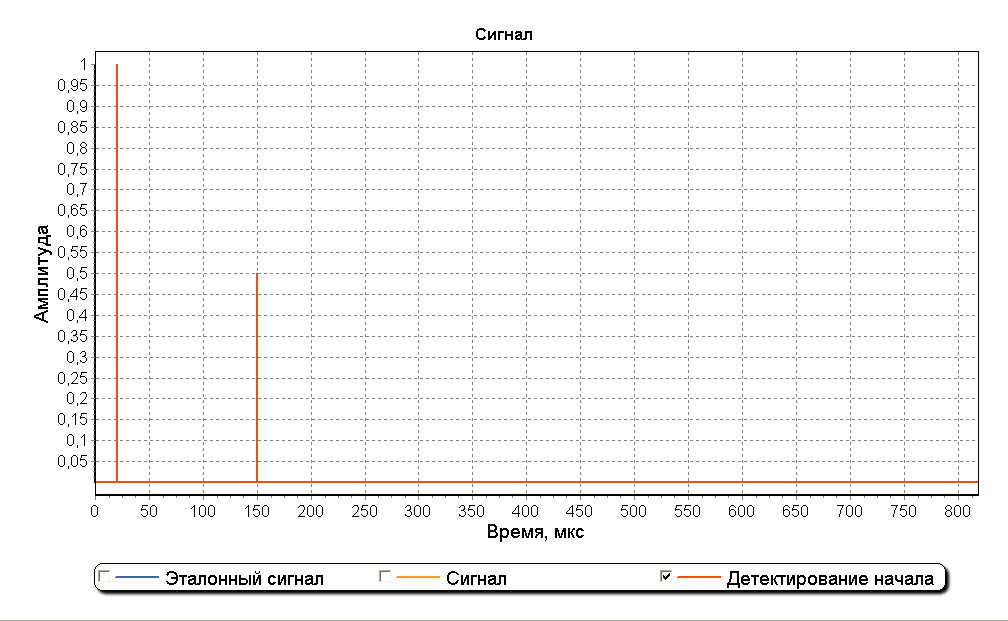
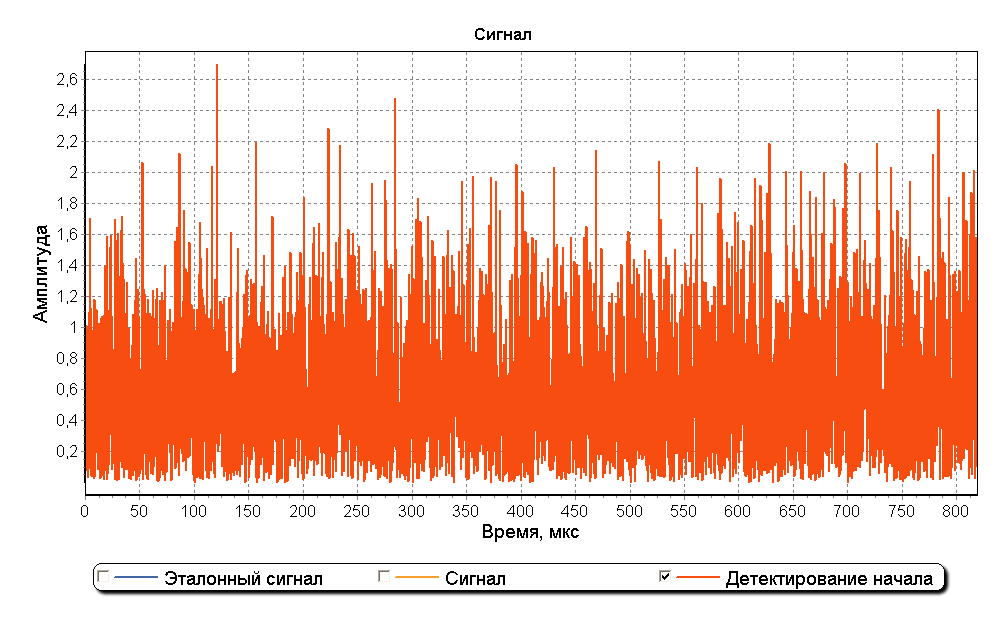
Метод обычного деления спектров хорошо действует для идеальных сигналов. При добавлении в сигнал шумовой составляющей эффективность метода резко ухудшается. На рисунках ниже изображен график детектирования начала сигнала при соотношении сигнал/шум 25 дБ. Как видно из рисунков определение начала сигналов выполнить невозможно.
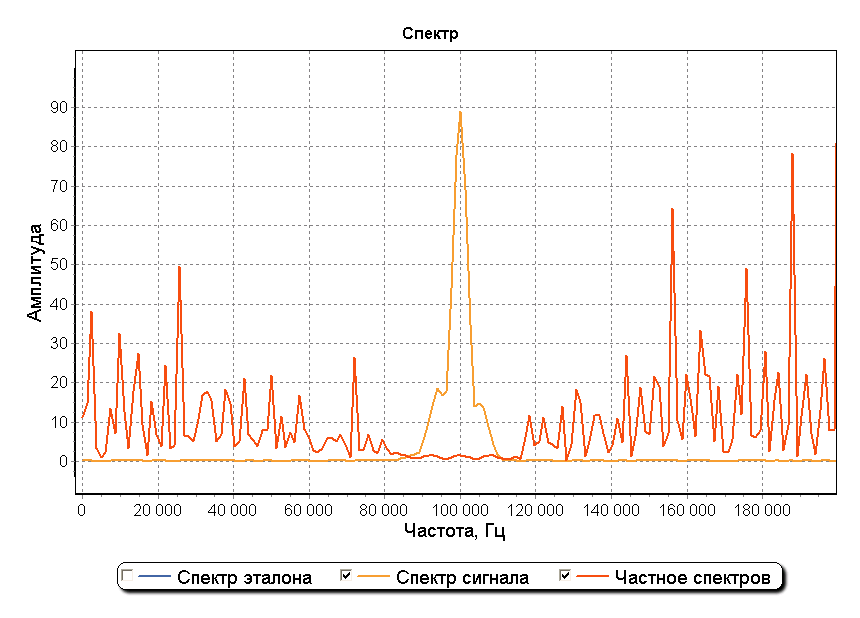
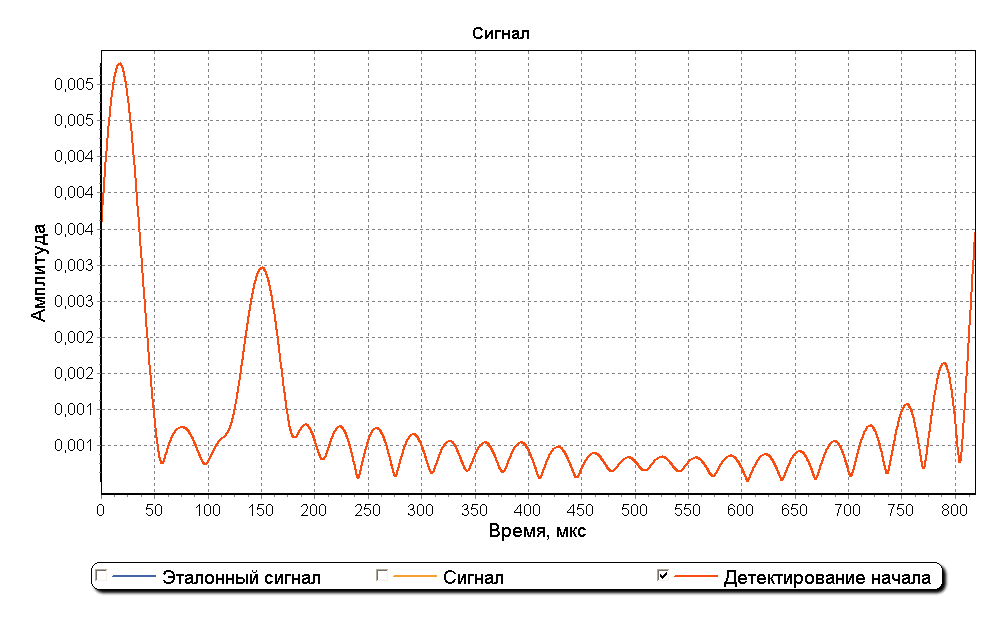
На графике спектра можно заметить, что внутри полосы шириной приблизительно 30 кГц с центром в точке 100 кГц результат деления спектров имеет горизонтальный пилообразный вид как при использовании метода деления спектров на идеальном не зашумленном сигнале. Использование прямоугольного окна шириной 30 кГц с центром в точке 100 кГц позволяет устранить влияние шумов перед операцией обратного преобразования Фурье. На рисунке ниже изображен график детектирования начала сигнала при использовании оконной фильтрации зашумленного сигнала. Два максимума графика позволяют обнаружить начало каждой из составляющих сигнала на фоне шума и также оценить отношение их амплитуд.
Метод деления спектров с применением оконного сглаживания эффективен при соотношении сигнал/шум выше 12 дБ. Наиболее эффективным типом окна признано прямоугольное окно с полосой 30 кГц. На рисунках ниже изображен реальный импульс цепочки Northern Sea of China Chain и график обнаружения его начала.
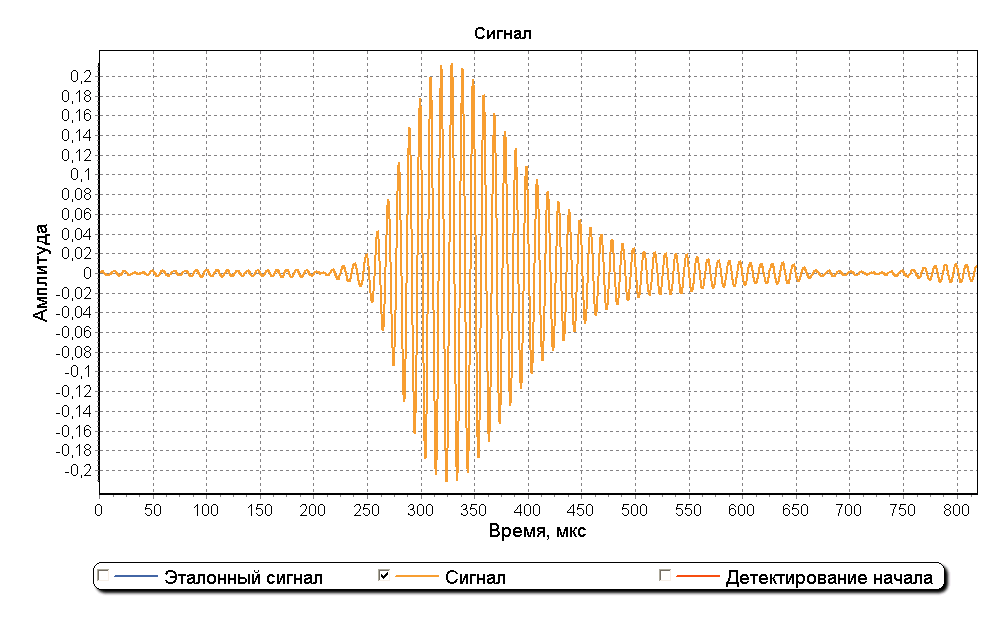
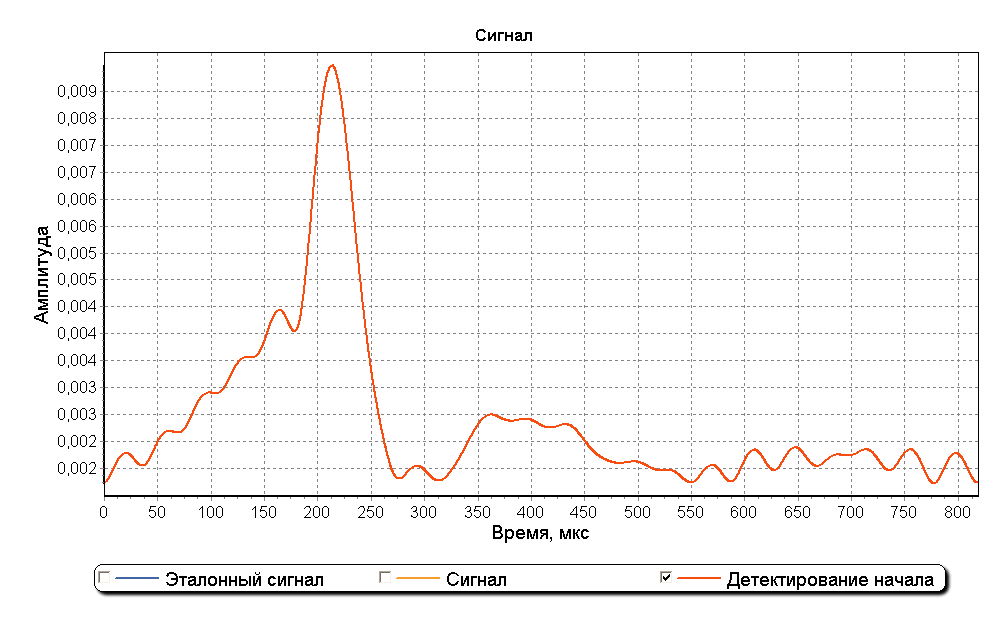
Оригинальная статья расположена здесь. Алгоритм в настоящее время применяется мной для контроля параметров станций ИФРНС Дальневосточного региона.
Автор: Dootch