Структура публикации
- Получение кватерниона из вектора и величины угла разворота
- Обратный кватернион
- Умножение кватернионов
- Поворот вектора
- Рысканье, тангаж, крен
- Серия поворотов
Получение кватерниона из вектора и величины угла разворота
Ещё раз – что такое кватернион? Для разработчика – это прежде всего инструмент, описывающий действие – поворот вокруг оси на заданный угол:
(w, vx, vy, vz),
где v – ось, выраженная вектором;
w – компонента, описывающая поворот (косинус половины угла).
Положительное значение угла разворота означает поворот вдоль вектора по часовой стрелке, если смотреть с конца вектора в его начало.
Например, кватернион поворота вдоль оси Х на 90 градусов имеет следующие значения своих компонент: w = 0,7071; x = 0,7071; y = 0; z = 0. Левая или правая система координат, разницы нет – главное, чтобы все операции выполнялись в одинаковых системах координат, или все в левых или все в правых.
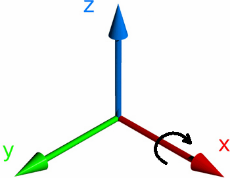
С помощью следующего кода (под ругой был Visual Basic), мы можем получить кватернион из вектора и угла разворота вокруг него:
Public Function create_quat(rotate_vector As TVector, rotate_angle As Double) As TQuat
create_quat.w = Cos(rotate_angle / 2)
create_quat.x = rotate_vector.x * Sin(rotate_angle / 2)
create_quat.y = rotate_vector.y * Sin(rotate_angle / 2)
create_quat.z = rotate_vector.z * Sin(rotate_angle / 2)
End Function
В коде rotate_vector – это вектор, описывающий ось разворота, а rotate_angle – это угол разворота в радианах. Вектор должен быть нормализован. То есть его длина должа быть равна 1.
Public Function normal(v As TVector) As TVector
Dim length As Double
length = (v.x ^ 2 + v.y ^ 2 + v.z ^ 2) ^ 0.5
normal.x = v.x / length
normal.y = v.y / length
normal.z = v.z / length
End Function
Не забывайте про ситуацию, когда длина может быть 0. Вместо ошибки вам может понадобиться обработать эту ситуацию индивидуально.
Обратный кватернион
Для поворота вектора кватернионом требуется уметь делать обратный разворот и правильно выполнять операцию умножения кватернионов. Под обратным разворотом я имею ввиду обратный кватернион, т. е. тот, который вращает в обратную сторону.
Чтобы получить обратный кватернион от заданного, достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион. Нормализация кватерниона так же как и в векторах, это просто приведение к длине = 1.
Public Function quat_scale(q As TQuat, val As Double) As TQuat
q.w = q.w * val ' x
q.x = q.x * val ' x
q.y = q.y * val ' y
q.z = q.z * val ' z
quat_scale = q
End Function
Public Function quat_length(q As TQuat) As Double
quat_length = (q.w * q.w + q.x * q.x + q.y * q.y + q.z * q.z) ^ 0.5
End Function
Public Function quat_normalize(q As TQuat) As TQuat
Dim n As Double
n = quat_length(q)
quat_normalize = quat_scale(q, 1 / n)
End Function
Public Function quat_invert(q As TQuat) As TQuat
Dim res As TQuat
res.w = q.w
res.x = -q.x
res.y = -q.y
res.z = -q.z
quat_invert = quat_normalize(res)
End Function
Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0). Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 градусов она = 0. Кватернион, который означает «нет разворота» = (w=1; x = 0; y = 0; z=0), то есть у него длина вектора оси = 0.
Умножение кватернионов
Умножение кватернионов крайне полезная штука. Результатом умножения является кватернион, который после поворота даёт такой же результат, если последовательно выполнить развороты умножаемыми кватернионами. Причём разворот будет происходить в локальной для поворачиваемого вектора системе отчёта, т. е. система отчёта поворачиваемого вектора также двигается.
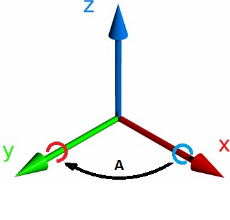
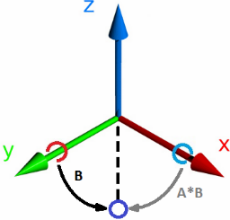
Умножение кватернионов выполняется следующим образом:
Public Function quat_mul_quat(a As TQuat, b As TQuat) As TQuat
Dim res As TQuat
res.w = a.w * b.w - a.x * b.x - a.y * b.y - a.z * b.z
res.x = a.w * b.x + a.x * b.w + a.y * b.z - a.z * b.y
res.y = a.w * b.y - a.x * b.z + a.y * b.w + a.z * b.x
res.z = a.w * b.z + a.x * b.y - a.y * b.x + a.z * b.w
quat_mul_quat = res
End Function
Для того, чтобы умножить кватернион на 3D вектор, нужно вектор преобразовать в кватернион присвоив компоненте W = 0 и умножить кватернион на кватернион. Или подставить ноль и выразить это в виде функции:
Public Function quat_mul_vector(a As TQuat, b As TVector) As TQuat
Dim res As TQuat
res.w = -a.x * b.x - a.y * b.y - a.z * b.z
res.x = a.w * b.x + a.y * b.z - a.z * b.y
res.y = a.w * b.y - a.x * b.z + a.z * b.x
res.z = a.w * b.z + a.x * b.y - a.y * b.x
quat_mul_vector = res
End Function
Поворот вектора
Теперь, собственно, поворот вектора кватернионом:
Public Function quat_transform_vector(q As TQuat, v As TVector) As TVector
Dim t As TQuat
t = quat_mul_vector(q, v)
t = quat_mul_quat(t, quat_invert(q))
quat_transform_vector.x = t.x
quat_transform_vector.y = t.y
quat_transform_vector.z = t.z
End Function
Пример:
Вектор описывающий ось (x=1; y=0; z=1). Угол поворота 180 градусов.
Поворачиваемый вектор (x=0; y=0; z=1). Результат равен (x=1; y=0; z=0).
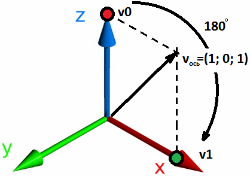
Рысканье, тангаж, крен
Рассмотрим инструмент формирования кватерниона с помощью поворотов вокруг одной из осей:
Рысканье = heading = yaw = вокруг оси Z; тангаж = altitude = pitch = вокруг оси Y; крен = bank = roll = вокруг оси X.
yaw = angles.altitude
pitch = angles.bank
roll = angles.heading
hr = roll * 0.5
shr = Sin(hr)
chr = Cos(hr)
hp = pitch * 0.5
shp = Sin(hp)
chp = Cos(hp)
hy = yaw * 0.5
shy = Sin(hy)
chy = Cos(hy)
chy_shp = chy * shp
shy_chp = shy * chp
chy_chp = chy * chp
shy_shp = shy * shp
res.w = (chy_chp * chr) + (shy_shp * shr)
res.x = (chy_shp * chr) + (shy_chp * shr)
res.y = (shy_chp * chr) - (chy_shp * shr)
res.z = (chy_chp * shr) - (shy_shp * chr)
quat_from_angles_rad = res
И в обратную сторону, из кватерниона:
k.bank = atan2(2 * (w * x + y * z), 1 - 2 * (sqx + sqy))
k.altitude = Application.WorksheetFunction.Asin(2 * (w * y - x * z))
k.heading = atan2(2 * (w * z + x * y), 1 - 2 * (sqy + sqz))
Серия поворотов
Рассмотрим пример:
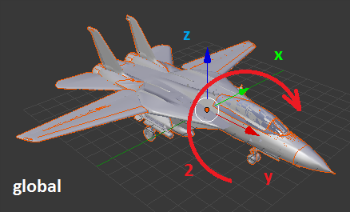
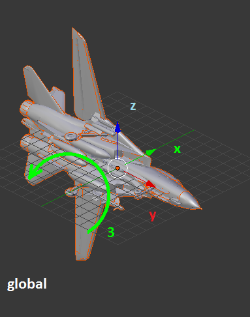
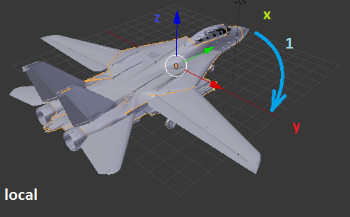
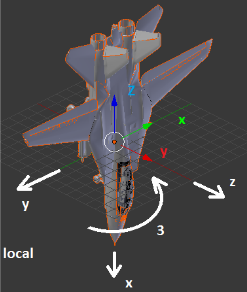
1. Первый поворот – рысканье (вокруг Z) 90 градусов по часовой;
2. Второй поворот – тангаж (вокруг Y) 90 градусов по часовой;
3. Третий поворот – крен (вокруг X) 90 градусов по часовой.
Рисунки, изображающие поворот и подписанные как «global» демонстрируют повороты относительно неподвижных осей XYZ. Такой результат мы получим, если будем использовать кватернионы разворота по отдельности. Четвёртый рисунок демонстрирует, где окажется вектор, если начальные координаты у него были X=1; Y=0; Z=0.
Рисунки, подписанные как «local» демонстрируют вращение осей вместе с самолетом. То есть все вращения происходят относительно пилота, а не относительно неподвижной системы координат. Четвёртый рисунок показывает, где окажется тот же самый вектор (1; 0; 0) в итоге всех трёх поворотов. Такой результат мы получим, перемножив кватернионы разворота и применив полученный кватернион.




Автор: 1div0





