В предыдущих статьях, посвященных вероятностному описанию конверсии сайта, мы рассматривали число событий (просмотров и кликов), как выборку случайной величины, без зависимости от времени. Теперь пришло время сделать следующий шаг и ввести ее в рассмотрение.
Случайные процессы
Случайный процесс f(t) – это, немного упрощая, случайная величина, зависящая от времени. Множество значений f(t) для некоторого промежутка времени T называют реализацией или выборкой случайного процесса. Например, количество просмотров страницы сайта за сутки – это пример дискретного случайного процесса (или случайной последовательности), для него и аргумент (время), и область значений, т.е. возможные значения f(t) – дискретные величины. Соответственно, выборкой случайного процесса будет вектор f(ti). Пример двух выборок случайных процессов приведены на графике (расчеты, как и все в моем блоге, подготовлены при помощи Mathcad Express и их вы можете взять здесь).
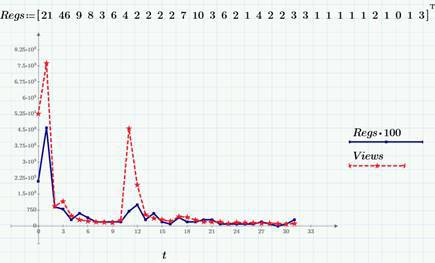
В качестве примеров мы по-прежнему используем данные по просмотрам (ряд Views, красный пунктир) и кликам (Regs, с множителем 100) в этом блоге на Хабре в марте 2015 г., которые мы подробно обсуждали здесь и здесь. В частности, во второй статье мы выяснили, что через несколько дней после выхода каждой статьи на Хабре число просмотров и кликов выходит на приблизительно постоянный уровень в 100-200 просмотров и 1-3 кликов в сутки, т.е. можно говорить о том, что после небольшого промежутка нестационарности, случайный процесс можно считать стационарным (в пренебрежении, конечно, слабым уменьшающимся трендом и поправкой на зависимость от дня недели, о чем, надеюсь еще поговорить в следующих статьях, когда дойдем до детрендинга). Следующий график – это стационарный «хвост» реализации числа просмотров (за конец марта 2015 г.).
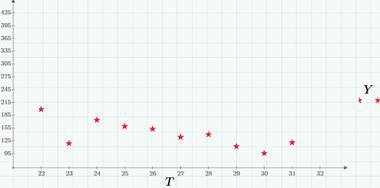
Как мы уже видим, классифицировать случайные процессы можно по характеру аргумента и значений (дискретные они или непрерывные). Как несложно сообразить, возможны четыре сочетания (подробнее об этом можно прочитать, например, в книге Тихонова «Статистическая радиотехника»). Пример дискретного процесса с непрерывным временем – это количество просмотров сайта (или кликов на сайте), начиная с некоторого момента времени (например, с момента публикации статьи). На следующем графике приведен пример реализации такого процесса – числа кликов в течение одного из дней (22 марта 2015 г.).
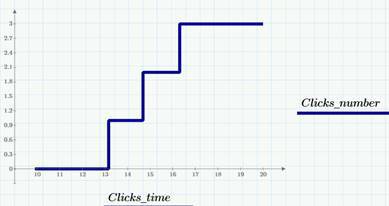
Что мы можем сказать о модели просмотров/кликов, глядя на последний график? Очевидно, мы имеем две последовательности случайных событий (событие А – просмотр и событие В – клик по некоторой ссылке), которые могут происходить в случайные моменты времени. Соответственно, случайный процесс b(t), реализация которого приведена на предыдущем графике, определяется, как число кликов, начиная с полуночи 22-го марта до времени t.
Вполне логично предположить, что для любого промежутка времени (например, час или сутки) вероятность наступления события (А или В) зависит только от длительности этого промежутка (это свойство называется однородностью случайного процесса во времени). Например, если за час происходит около 6 просмотров статьи, то за сутки их будет около 6*24~140. Или, если в день происходит в среднем 2 клика, то условно можно сказать, что среднее число кликов в час равно 1/12. На гистограмме показан разброс значений числа просмотров, соответствующий «хвосту». Выборочные средние значения составляют λ=140 просмотров и λ2=1.2 клика (в сутки).
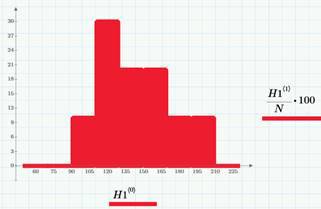
Здесь важно сделать несколько оговорок. Во-первых, такой подход носит исключительно вероятностный характер. Мы заранее не знаем ни точного числа кликов в день, ни моментов, в которые будут происходить клики. Во-вторых, кое-что о ситуации мы все-таки знаем: что около 140 человек открывают в день статью и 1-3 из них кликают в определенном месте статьи. В-третьих, конечно, в данных будет присутствовать суточный тренд (днем статью читают гораздо больше, нежели ночью). Для простоты (и до поры до времени – когда дойдем до детрендинга), им тоже будем пренебрегать. И, в четвертых (внимание!), пока мы не говорим о том, чему равна вероятность событий А и В (просмотров и кликов).
Пуассоновский поток событий
Как известно из теории вероятностей, сформулированной моделью, называемой случайным процессом Пуассона или пуассоновским потоком событий, неплохо описываются не только просмотры и клики, но и огромное число других реальных явлений: телефонные звонки, отказы техники (скоро про это здесь будет отдельная статья), запросы на обслуживание и т.д. Если условится считать выборочную функцию непрерывной справа, то, как и показано на соответствующем рисунке сверху, она будет целочисленной, причем возрастающей только целочисленными скачками. Соответственно, плотность вероятности числа кликов и просмотров будет дискретной, как показано на рисунке (для случая кликов, ряд в виде красных «палок»):
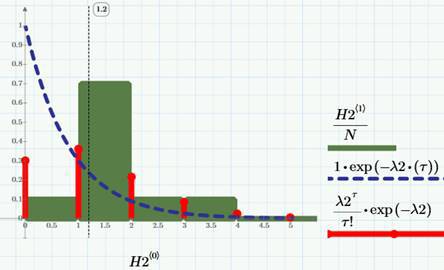
На том же рисунке «столбиками» (что наглядно, но немного неправильно, т.к. речь идет о дискретном процессе) показана соответствующая гистограмма распределения по числу кликов, а о смысле пунктирной кривой скажем чуть позже. Формула для плотности вероятности Пуассона приведена на графике (в легенде «палок»). Таким образом – внимание! – вычислив выборочное среднее значение числа кликов λ2=1.2 (клика в сутки), мы получаем инструмент для прогноза, а, рассматривая его вместе с данными по конверсии (см. предыдущие статьи), получаем алгоритм расчета необходимого числа посещений для достижения определенных целевых показателей по кликам.
Еще одна важная величина, характеризующая процесс Пуассона – это время ожидания первого события τ. Очевидно, что τ – это случайная величина. Из теории вероятностей известно, что ее функция распределения – экспоненциальная и задается формулой F(t)=P(τ<t)=1-exp(-λt). Соответственно, событие, заключающееся в том, что клика (или просмотра) еще не произошло, характеризуется функцией распределения
1-F(t)=exp(-λt). Для наглядности, мы нарисуем эту функция распределения на графике, выбрав в качестве единиц измерения времени часы (а не сутки). Синяя кривая P(t) относится к просмотрам, а красная к кликам.
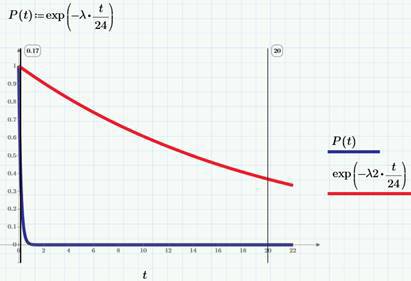
Соответственно, плотность вероятности времени ожидания запишется следующем образом:
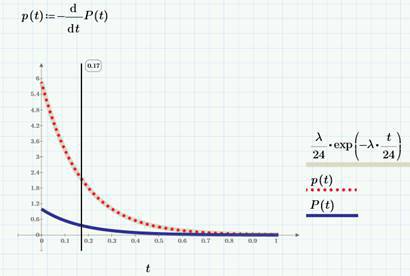
Плотность распределения числа просмотров мы обозначили функцией p(t), чтобы напомнить о связи плотности распределения и плотности вероятности случайной величины.
Как несложно вычислить, среднее значение времени ожидания первого клика равняется 1/λ2, а просмотра, соответственно, 1/λ, что дает представление о простом вероятностном смысле параметра λ, как среднего числа событий происходящих в единицу времени и равного среднему времени ожидания первого события.
Ссылки:
- Пытьев Ю.П., Шишмарев И.А.
Курс теории вероятности и математической статистики для физиков. М.: МГУ, 1983 - Тихонов В.И. Статистическая радиотехника М: «Советское радио», 1966
- Д.В. Кирьянов, Е.Н. Кирьянова. Вычислительная физика. М: Полибук Мультимедиа, 2005. §5. Случайные процессы и поля
Автор: polybook






