Привет!
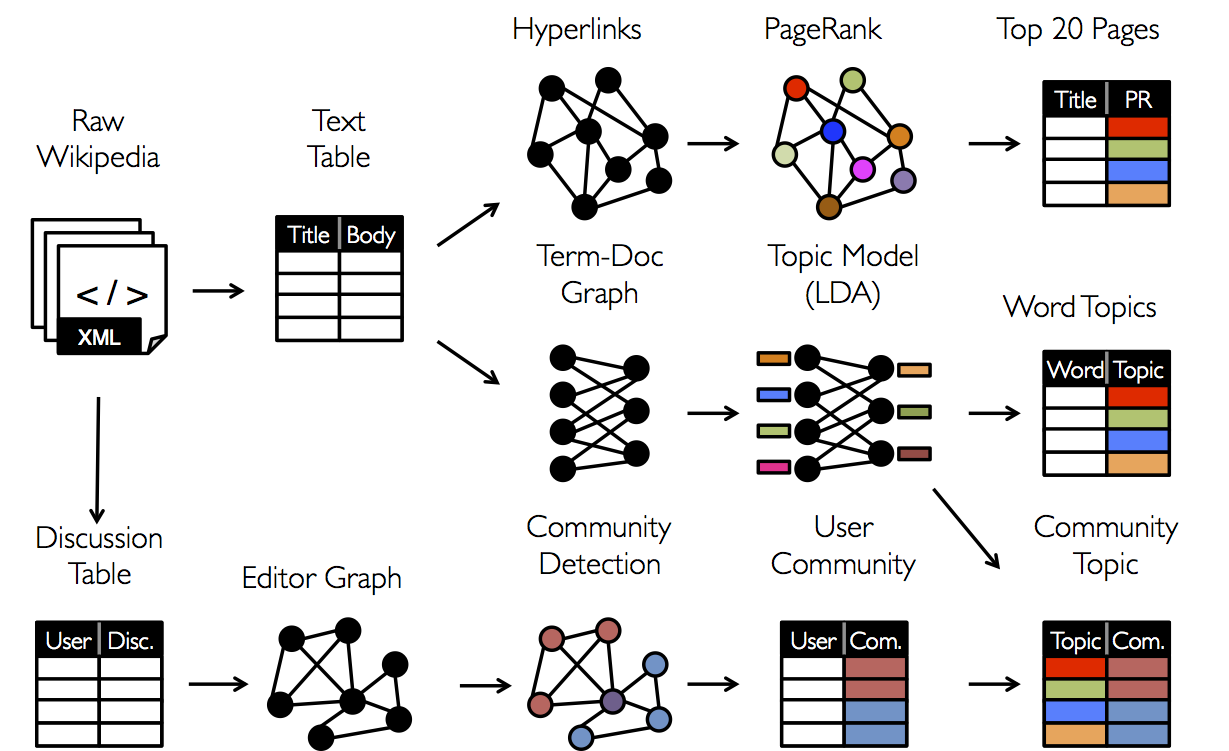
Сегодня мы подробно познакомимся с задачами Анализа Социальных Сетей (SNA), а также закончим обзор библиотеки Apache Spark, предназначенной для анализа Больших Данных. А именно, как и было обещано в предыдущих статьях (раз и два) мы рассмотрим одну из компонент Apache Spark, предназначенную для анализа графов — GraphX. Постараемся понять, как в этой библиотеке реализовано распределенное хранение графов и вычисления на них. А также покажем на конкретных примерах, как данная библиотека может использоваться на практике: поиск спама, ранжирование поисковой выдачи, выделение сообществ в социальных сетях, поиск лидеров мнения — далеко не полный список применений методов анализа графов.
Итак, начнем с того, что напомним (для тех, кто не погружен в теорию графов) основные обьекты, с которыми мы будем работать в данной статье и погрузимся в алгоритмы и всю красивую математику, которая за этим стоит.
Теория графов, случайные и веб-графы
Наверное, лучше всего в этом разделе отправить читателя смотреть замечательные видео-лекции и брошюры моего научного руководителя Андрея Михайловича Райгородского, например, вот тут — никто лучше него так понятно и доступно об этом не расскажет. Очень рекомендуется просмотреть также вот это или это. А еще лучше — записаться на курс Андрея Михайловича на Coursera. Поэтому здесь лишь дадим основные понятия и не будем вдаваться в детали.
Граф — это пара G = (V,E) — где, V — множество вершин (скажем, сайты в интернете), а E — множество ребер, соединяющих вершины (соответственно, ссылки между сайтами). Вполне понятная структура, анализом которой занимаются уже много лет. Однако, на практике при анализе реальных сетей возникает возникает вопрос — а как этот граф строится? Скажем, появляется новый сайт в интернете — на кого он будет ссылать в первую очередь, сколько в среднем появится новых ссылок, насколько хорошо будет ранжироваться этот сайт в поисковой выдаче?
Этой задачей (устройством веб-графа) люди занимаются почти с момента появления Интернета. За это время было придумано немало моделей. Не так давно в Яндексе была предложена обобщенная модель, а также исследованы ее свойства.
Если же граф нам уже дан — его свойства, а также дальнейшие вычисления на графе вполне определены. Например, можно исследовать как себя степень конкретной вершины (количество друзей человека в социальной сети), либо мерить расстояния между конкретными вершинами (через сколько рукопожатий знакомы 2 заданных человека в сети), вычислять компоненты связности (группа людей, где по «связям» между людьми любые 2 человека знакомы) и многое другое.
Классическими алгоритмами являются:
PageRank — известный алгоритм вычисления «авторитетности» вершины в графе, предложенный Google в 1998 году и долгое время используемый для ранжирования поисковой выдачи
Поиск (сильно) связных компонент — алгоритм поиска подмножеств вершин графа таких, что между любыми двумя вершинами из конкретного подмножества существует путь, и не существует путей между вершинами разных подмножеств
Подсчет кратчайших путей в графе — между любой парой вершин, между конкретными двумя вершинами, на взвешенных графах и в других постановках
А также подсчет числа треугольников, кластеризация, распределение степеней вершин, поиск клик в графе и многое другое. Стоит отметить, что большинство алгоритмов являются итеративными, и поэтому, в данном контексте очень хорошо показывает себя библиотека GraphX ввиду того, что кэширует данные в оперативной памяти. Далее, мы рассмотрим, какие возможности нам предоставляет данная библиотека.
Spark GraphX
Сразу отметим, что GraphX — далеко не первый и не единственный инструмент для анализа графов (известными инструментами, являются, например, GraphLab — нынешний Dato.com или Pregel — на котором GraphX и основан), а также то, что на момент написания данного поста библиотека находилась еще в разработке и возможности ее не так велики. Тем не менее, практически для любых задач, которые возникают на практике свое применение GraphX так или иначе оправдывает.
В GraphX пока нет поддержки Python, поэтому код будем писать на Scala, предполагая, что уже создан SparkContext (в коде ниже — переменная sc). Большая часть кода ниже взята из документации и открытых материалов. Итак, для начала загрузим все необходимые библиотеки:
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD
В спарке концепция графа реализована в виде так называемого Property Graph — это мультиграф с метками (дополнительной информацией) на вершинах и ребрах. Мультиграф — это ориентированный (ребра имеют направления) граф, в котором разрешены кратные ребра (может быть несколько ребер между двумя вершинами), петли (ребро из вершины в саму себя). Тут же скажем, что в случае ориентированных графов — определены такие понятия, как входящая степень (число входящих ребер) и исходящая степень (число исходящих из вершины ребер). Посмотрим на примерах, как можно построить конкретный граф.
Построение графа
Построить граф можно с помощью конструктора Graph, передав на вход массивы вершин и ребер из локальной программы (не забыв сделать из них RDD с помощью функции .parallelize()):
val vertexArray = Array(
(1L, ("Alice", 28)),
(2L, ("Bob", 27)),
(3L, ("Charlie", 65)),
(4L, ("David", 42)),
(5L, ("Ed", 55)),
(6L, ("Fran", 50))
)
val edgeArray = Array(
Edge(2L, 1L, 7),
Edge(2L, 4L, 2),
Edge(3L, 2L, 4),
Edge(3L, 6L, 3),
Edge(4L, 1L, 1),
Edge(5L, 2L, 2),
Edge(5L, 3L, 8),
Edge(5L, 6L, 3)
)
val vertexRDD = sc.parallelize(vertexArray)
val edgeRDD = sc.parallelize(edgeArray)
val graph = Graph(vertexRDD, edgeRDD)
Либо, если вершины и ребра сначала необходимо построить на основе каких-то данных, лежащих, скажем в HDFS, небходимо сначала обработать сами исходные данные (как это часто бывает — с помощью .map() — преобразования). Например, если у нас есть статьи из Википедии, хранящиеся в виде (id, title), а также ссылки между статьями, хранящиеся в виде пар, то граф строится довольно легко — для этого надо отделить id от title в первом случае и сконструировать сами ребра (для этого есть конструктор Edge) — во втором случае, на выходе получив список вершин и ребер, которые можно передать конструктору Graph:
val articles = sc.textFile("articles.txt")
val links = sc.textFile("links.txt")
val vertices = articles.map { line =>
val fields = line.split('t')
(fields(0).toLong, fields(1))
}
val edges = links.map { line =>
val fields = line.split('t')
Edge(fields(0).toLong, fields(1).toLong, 0)
}
val graph = Graph(vertices, edges, "").cache()
После построения графа для него можно вычислять некоторые характеристики а также запускать на нем алгоритмы, в том числе и перечисленные выше. Пока мы не продолжили, стоит отметить здесь, что в спарке помимо концепции вершин и ребер реализовано также понятие триплет (Triplet) — это обьект, который в некотором смысле немного расширяет обьект ребро (Edge) — в нем хранится помимо информации о ребре также информация о вершинах, к нему примыкающих.
Вычисления на графах
Замечательный факт заключается в том, что в большинстве пакетов (и GraphX в этом не является исключением) — после построения графа становится легко делать на нем вычисления, а также запускать стандартные алгоритмы. Действительно, сами по себе методы вычисления на графах изучены достаточно хорошо, и в конкретных прикладных задачах самое сложное — это правило определить граф, а именно — определить, что является вершинами, а что — ребрами (на каком основании их проводить). Ниже приведем список некоторых доступных методов у обьекта Graph с комментариями:
class Graph[VD, ED] {
// Базовые статистики графа
val numEdges: Long // количество ребер
val numVertices: Long // количество вершин
val inDegrees: VertexRDD[Int] // входящие степени вершин
val outDegrees: VertexRDD[Int] // исходящие степени вершин
val degrees: VertexRDD[Int] // суммарные степени вершин
// Отдельные представления вершин, ребер и триплетов
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
// Изменение атрибутов (дополнительной информации) у вершин и ребер
def mapVertices[VD2](map: (VertexID, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
// Модификации графов
def reverse: Graph[VD, ED] // обращение - все ребра меняют направление на противоположное
def subgraph(
epred: EdgeTriplet[VD,ED] => Boolean = (x => true),
vpred: (VertexID, VD) => Boolean = ((v, d) => true))
: Graph[VD, ED] // выделение подграфов, удовлетворяющих определенным условиям
def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED] // слияние ребер
// Базовые графовые алгоритмы
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double] // вычисление PageRank
def connectedComponents(): Graph[VertexID, ED] // поиск компонент связности
def triangleCount(): Graph[Int, ED] // подсчет числа треугольников
def stronglyConnectedComponents(numIter: Int): Graph[VertexID, ED] // поиск сильных компонент связности
}
Стоит отметить, что в текущая реализация SparkX содержит довольно мало реализованных алгоритмов, поэтому пока еще остается актуальным использование перечисленных выше известных пакетов вместо Apache Spark, однако, есть уверенность, что GraphX в будущем будет существенно доработан, а благодаря возможности кэширования данных в оперативной памяти, вероятно, получит достаточную популярность в графовых задачах. В заключение, приведем примеры практических задач, где приходится применять графовые методы.
Практические задачи
Как было сказано выше — основная проблема в практических задачах заключается больше не в том, чтобы запустить сложные алгоритмы — а именно в правильном определении графа, в его правильной предобработки и сведении задачи к классической решенной. Рассмотрим, это на примерах, где оставим читателю большое количество вопросов для размышления:
Прогнозирование появляения нового ребра (Link Prediction)
Задача достататочно распространенная — дана последовательность ребер, которые добавляются в граф до какого-то момента. Необходимо предсказать, какие ребра появятся в будущем в нашем графе. С точки зрения реальной жизни — эта задача представляет собой часть рекомендательной системы — например, прогнозирование связей («дружбы») между двумя пользователями соц. сети. В этой задаче фактически надо для каждой пары произвольно выбранных вершин предсказать — какова вероятность того, что между ними в будущем будет ребро — тут как раз нужно работать с признаками и с описанием вершин. Например, в качестве одного из признаков может быть пересечение множеств друзей, либо мера Жаккарда. Читателю предлагается подумать над возможными метриками сходства между вершинами и написать свой вариент в комментариях).
Выделение сообществ в социальных сетях
Задача, которую сложно отнести к какому-то конкретному задач. Зачастую она рассматривается в контексте задачи «кластеризации на графах». Методов решения тут масса — от простого выделения компонент связности (алгоритм упоминался выше) при правильно определенном подмножестве вершин, до последовательного удаления ребер из графа до тех пор пока не останется нужная компонента. Здесь, опять же — очень важно сперва понимать, какие именно сообщества мы хотим выделять в сети, т.е. сперва поработать с описанием вершин и ребер, а уже потом думать, как в полученном подграфе выделять сами сообщества.
Кратчайшие расстояния на графах
Это задача является также классической и реализована, например, в том же Яндекс.Метро или других сервисах, которые помогают найти кратчайшие пути в некотором графе — будь то граф связей между точками города или граф знакомств.
Или задача, с которой легко может столкнуться, например, сотовый оператор:
Определение лидеров мнения в сети
Для продвижения, скажем, некоторой новой опции, например мобильного интернете, с целью оптимизации рекламного бюджета хотелось бы выделить людей, которые в некотором смысле окружены вниманием со стороны. В наших терминах — это вершины графа, имеющие большую авторитетность в сети — поэтому данная задача при правильном построении графа сводится к задаче PageRank.
Итак, мы рассмотрели типичные прикладные задачи анализа графов, которые могут возникать на практике, а также один из инструментов, который можно применять для их решения. На этом мы заканчиваем обзор библиотеки Apache Spark, да и вообще обзор инструментов и в будущем сосредоточимся больше на алгоритмах и конкретных задачах!
Автор: akrot

