
Данная статья посвящена описанию работы с пакетом PGFPlots, разработанного для популярной настольной издательской системы LaTeX. Однако, если вы даже не знакомы с последней, это не повод расстраиваться и бросать чтение этой статьи, ведь, возможно, те замечательные примеры, которые будут далее приведены, и необычайная мощность и удобство PGFPlots вдохновят вас на изучение LaTeX.
Введение и мотивация
Существует большое число различных систем для построения графиков и визуализации данных. Конечно, нельзя сказать, что PGFPlots может заменить их все (например, при работе со средой R иногда удобнее положится на её собственный механизм построения графиков и просто добавлять построенные графики в документ как изображения), однако существует определенная и значительная ниша, в которой применять его удобно: учебные материалы; различные отчёты, которые будучи студентами, наверно делали все в той или иной мере; простейшая визуализация данных и т.п.
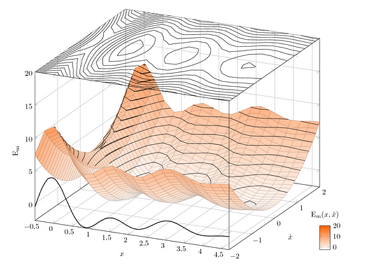
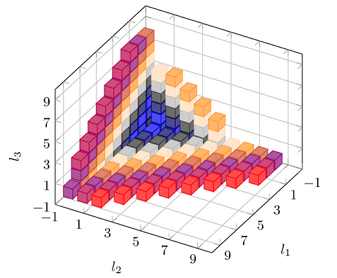
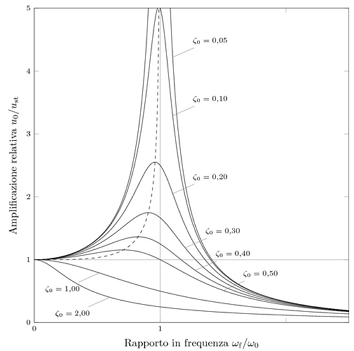
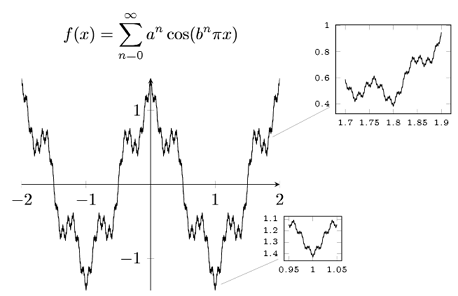
Ниже показаны примеры, которые не только подтверждают сказанное, но и показывают, что возможности данной системы зачастую даже превосходят наши повседневные требования к такого рода системам (щелкните на изображение, чтобы посмотреть исходник примера):
 |
 |
 |
 |
Статья не претендует на роль исчерпывающего руководства по PGFPlots, поскольку с такой ролью успешно справляется официальная документация, на которую в дальнейшем часто будут встречаться ссылки), скорее её роль в том, чтобы познакомить читателей с этой системой и хоть немного раскрыть основные её возможности. Выражаю надежду, что с этой задачей данная статья справится, а так это или не так, решать вам, читателям.
Для работы с примерами потребуется установленный дистрибутив LaTeX. К сожалению, его установка и настройка выходят за рамки данной статьи, поэтому те, кто не желает возиться с его установкой и настройкой, но хотят поэкспериментировать с возможностями, описанными здесь, могут попробовать такие онлайн-сервисы, как Overleaf и ShareLaTeX.
Итак, начнём!
Подключение пакета
Для подключения PGFPlots достаточно добавить в преамбулу документа команду:
usepackage{pgfplots}
После этого пакет будет загружен и установлен. Однако если же этого у вас по тем или иным причинам не происходит, то следует обратиться к документации (стр.11), где подробно расписаны различные способы установки данного пакета.
Кроме того, следует обратить внимание на то, что PGFPlots проектировался с расчётом на обратную совместимость, и проекты, созданные с использованием старых версий данного пакета будут открываться и отображаться без изменений, вне зависимости от того, насколько новая версия стоит у вас. Однако в пакет, тем не менее, вносятся изменения, которые нарушают обратную совместимость и для того, чтобы их подключить, необходимо в преамбуле прописать явным образом используемую версию (в примере ниже указана версия 1.9):
pgfplotsset{compat=1.9}
Основы построения графиков
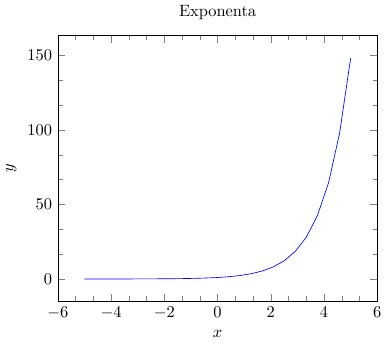
Рассмотрим сначала простейший пример построения графика и на нём объясним назначение основных компонентов, из которых состоит практически любой график в PGFPlots:
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[
title = Exponenta,
xlabel = {$x$},
ylabel = {$y$},
minor tick num = 2
]
addplot[blue] {e^x};
end{axis}
end{tikzpicture}
end{document}
Окружение tikzpicture
Поскольку PGFPlots базируется на основе TikZ (это ещё один замечательный пакет, предназначенный для создания графических изображений в LaTeX), то любой график размещается в соответствующем окружении tikzpicture данного пакета.
begin{tikzpicture} ... end{tikzpicture}
Следует отметить, что такая тесная связь TikZ и PGFPlots – это большой плюс, поскольку она позволяет, во-первых, очень хорошо интегрировать графики в различные рисунки, выполненные в TikZ, а также, наоборот, использовать возможности TikZ при работе с графиками (см. наглядный пример).
Окружение, устанавливающее оси графика
Далее, внутри указанного выше окружения, размещается ещё одно окружение, определяющее оси графика. Ниже в таблице перечислены основные виды таких окружений:
| Тип окружения | Назначение |
| axis | Стандартные оси с линейным масштабированием |
| semilogxaxis | Логарифмическое масштабирование оси x и стандартное масштабирование оси y |
| semilogyaxis | Логарифмическое масштабирование оси y и стандартное масштабирование оси x |
| loglogaxis | Логарифмическое масштабирование обеих осей |
Обычно многие настройки отображения графиков указываются в свойствах данного окружения (в примере выше указан заголовок title, название подписи к оси абсцисс xlabel, название подписи к оси ординат ylabel и количество дополнительных – в том смысле, что они не подписываются – делений между основными minor tick num). При этом следует понимать, что опции могут быть указаны не только таким образом (локально), но также и более глобально, например, при помощи стилей или путём добавления в преамбулу документа строчки, как показано в примере ниже:
pgfplotsset{title = Undefined chart}
Таких свойств – превеликое множество, они позволяют настроить практически любой аспект внешнего вида графика и все они перечислены в руководстве. Приведём для примера ниже список наиболее типичных для рассматриваемого окружения свойств:
| Свойство | Назначение | Возможные значения |
| width, height | Устанавливают ширину и высоту графика соответственно | |
| domain = min:max | Устанавливает область значений для функции в диапазоне от min до max | |
| xmin, xmax | Устанавливают минимальное и максимальное значение на оси абсцисс соответственно | |
| ymin, ymax | Устанавливают минимальное и максимальное значение на оси ординат соответственно | |
| xlabel, ylabel | Устанавливают подпись к оси абсцисс и оси ординат соответственно | |
| view | Устанавливает поворот камеры, при этом свойство указывается следующим образом view = {азимут}{угол возвышения}; при этом азимут – это угол между положением камеры и осью z, а угол возвышения – это угол между положением камеры и осью x. | |
| grid | Указывает тип сетки | major – линии сетки проходят только через основные деления, minor – линии сетки проходят через дополнительные деления (между основными), both – линии сетки проходят через оба вида делений, none – сетка отсутствует [по умолчанию] |
| colormap | Устанавливает используемую цветовую схему | hot, hot2, jet, blackwhite, bluered, cool, greenyellow, redyellow, violet и другие, созданные пользователем |
Добавление графика
Напомним, что в рассмотренном примере график добавлялся при помощи команды addplot, у которой в качестве основного параметра была указана функция, чей график был построен, и цвет данного графика:
addplot[blue] {e^x};
Использованная команда addplot (для двумерного графика) и её аналог addplot3 (для трёхмерного графика) являются наиболее распространенным средством для того, чтобы создать график. Общий формат данной команды следующий:
addplot[<options>] <input data> <trailing path commands>;
Опции <options> являются необязательным параметром, в которых указываются: тип графика, его цвет, стиль, тип маркеров и т.п.
Входные данные <input data> определяют на основании чего будет строится график, в примере в качестве входных данных была указана функция, однако, как будет показано далее, выбор входных данных гораздо шире.
Как небольшой итог
Итак, подведём небольшой итог нашего знакомства с PGFPlots.
- Все графики размещаются в окружение tikzpicture:
begin{tikzpicture} ... end{tikzpicture} - Для отображения графика, необходимо создать окружение, определяющего тип используемых осей в нём, например, axis:
begin{axis} ... end{axis} - Затем внутри созданного окружения добавляются графики чаще всего при помощи команд addplot и addplot3:
addplot[<options>] <input data> <trailing path commands>;
Входные данные
Не имея никакого желания, дублировать написанное в документации (стр.40 — 63) и излагать все тонкости работы со входными данными, мы остановимся на рассмотрении основных способов в наиболее общем виде, и приведём ряд примеров их поясняющих.
Построение графиков на основе математического выражения
Общий вид команды построения графика на основе математического выражения должен быть уже знаком:
addplot[<options>] {math_expression} <trailing path commands>; Для обработки математического выражения используется встроенный парсер, который имеет достаточный близкий синтаксис к многим системам компьютерной алгебры, и поэтому работа с ним не представляет особой сложности. Полный список математических операторов и функций можно найти в этом документе (стр.933). Часть из них для составления общего впечатления приведена ниже.
| Оператор | Назначение |
| + | Оператор сложения |
| - | Оператор вычитания |
| * | Оператор умножения |
| / | Оператор деления |
| ^ | Оператор возведения в степень |
| mod | Оператор взятия остатка |
| ! | Постфиксный оператор вычисления факториала |
| <, >, ==, <=, >= | Операторы сравнения |
| Функция | Назначение |
| abs | Функция взятия модуля |
| sin, cos, tan, asin, acos, atan | Основные тригонометрические функции и обратные им |
| ln, log2, log10 | Натуральный, двоичный и десятичный логарифмы |
| deg | Функция преобразования радиан в градуса (она особенно полезна, если учесть, что по умолчанию рассматриваемый парсер работает именно с градусами, а не радианами) |
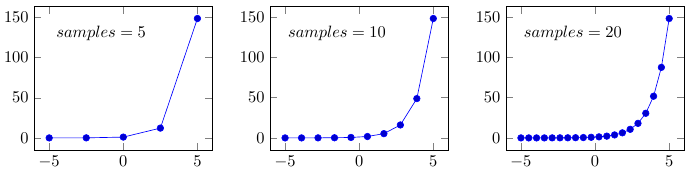
После того, как математическое выражение будет обработано, фактически, будет построено множество точек (количество этих точек можно изменить при помощи свойства графика samples), на основе которых будет построен тот или иной график. Как иллюстрация сказанного, ниже приведены одинаковые графики с различным значением свойства samples:
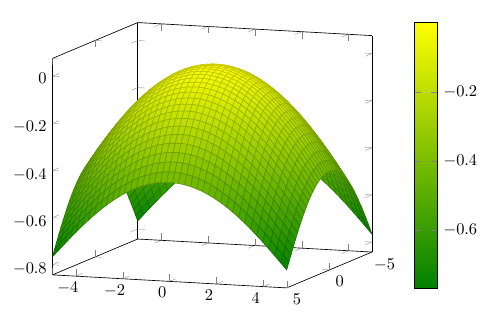
Ниже приведён пример построения 3D графика на основе математического выражения:
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[
view={110}{10},
colormap/greenyellow,
colorbar
]
addplot3[surf] {-sin(x^2 + y^2)};
end{axis}
end{tikzpicture}
end{document}
Заметьте, что здесь использовалась ранее не упомянутая команда colorbar , которая добавляет шкалу, устанавливающую соответствие между цветом и значением функции.
Построение графиков на основе вводимых координат
Данный способ гораздо проще, чем предыдущий и подразумевает, что пользователь просто укажет список упорядоченных пар (x,y) (для двумерного графика) или (x,y,z) (для трёхмерного графика) и на их основе впоследствии будет построен график.
addplot[<options>] coordinates {<coordinate list>} <trailing path commands>
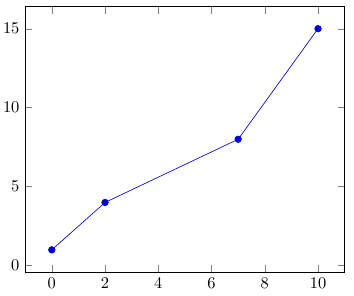
Сразу рассмотрим пример:
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}
addplot coordinates {
(0,1) (2,4) (7,8) (10,15)
};
end{axis}
end{tikzpicture}
end{document}
Обратите внимание на то, что упорядоченные пары просто разделяются пробелами без использования каких-либо специальных символов-разделителей.
Построение графиков на основе таблицы
Построение графиков на основе таблицы является одним из очень распространенных и удобных способов построения различных графиков.
addplot table [<column selection>] {(file or inline table)}.
В первую очередь, определим основные принципы работы с таблицами:
- Строки разделяются символов перехода на новую строку. Для использования в такой роли символа \ необходимо установить следующее свойство:
table/row sep = \ - Столбцы обычно разделяются пробелами или символами табуляции. Установить эту роль для других символов можно при помощи следующего свойства:
table/col sep = space|tab|comma|colon|semicolon|braces|&|ampersand - Любая строчка, начинающаяся с # или % будет проигнорирована
Пример корректной таблицы приведен ниже:
a b c
1 1 1
2 3 4
3 5 5
4 8 6
5 2 7
Параметр <column selection> определяет соответствие между определенной осью (или источником мета-информации, о которой мы чуть-чуть скажем позже) и столбцом, причем соответствие задаётся по первой строчке таблицы, что наглядно видно в примерах далее.
Построение графика на основе встроенной таблицы (inline)
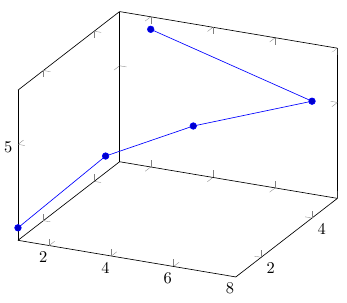
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}
addplot3 table [x = b, y = a, z = c] {
a b c
1 1 1
2 3 4
3 5 5
4 8 6
5 2 7
};
end{axis}
end{tikzpicture}
end{document}
Построение графика на основе таблицы во внешнем файле
Рассмотрим более практический пример. По следующей ссылке лежит файл .csv, в котором содержатся данные о демографической ситуации в России (РСФСР) за примерно век её истории.
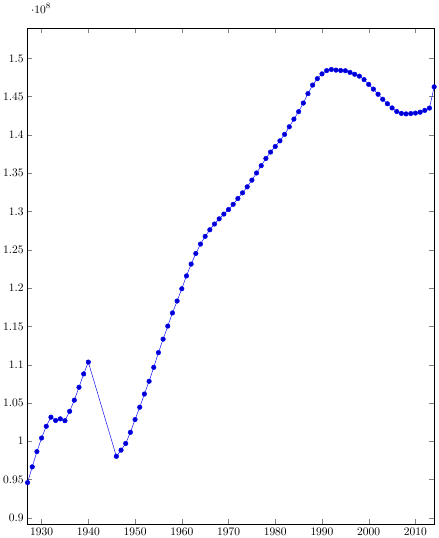
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[
table/col sep = semicolon,
height = 0.6paperheight,
width = 0.65paperwidth,
xmin = 1927,
xmax = 2014,
/pgf/number format/1000 sep={}
]
addplot table [x={Year}, y={Average population}]
{RussianDemography.csv};
end{axis}
end{tikzpicture}
end{document}
Естественно, что это далеко не все способы, и пока за гранью нашего рассмотрения осталось взаимодействия PGFPlots с другими приложениями (например, GNUPlot), использование скриптов при построении графиков, внедрение внешней графики и т.п.
Настройка графиков
Теперь, когда мы разобрались с тем, как могут выглядеть входные данные для графика, пора уделить внимание тому, как настроить графики, сделать их более понятными и наглядными.
Легенда графика
Легендой называется подпись, поясняющая то, что изображено на графике. Особенно полезно использование легенды, когда у нас имеется несколько различных графиков.
Для описание легенды можно использовать команду legend{...}, внутри которой через запятую перечисляются описания графиков (PGFPlots определяет соответствие между описанием и графиком по порядку следования описаний и порядку добавления самих графиков).
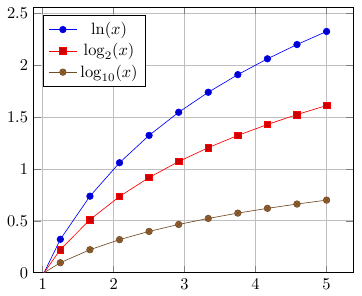
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis} [
legend pos = north west,
ymin = 0,
grid = major
]
legend{ $ln(x)$,
$log_2(x)$,
$log_{10}(x)$
};
addplot {log2(x)};
addplot {ln(x)};
addplot {log10(x)};
end{axis}
end{tikzpicture}
end{document}
В примере в легенде указаны математические выражения, на основе которых строятся данные графики, но, вообще, там может быть произвольный текст.
Кроме того, в нём использовалось свойство legend pos, которое позволяет указать положение легенды на графике (south west, south east, north west, north east, outer north east ).
Пользовательские стили
Рассмотрим простейший пример: у нас в документе принято, чтобы график, отражающий экспериментальные данные, выделялся красным цветом, а график функции, отражающий графики математической модели, имел синий цвет. Так было принято ровно до тех пор, пока в издательстве нам не сказали, что они принимают только черно-белые статьи и, соответственно, внешний вид графиков необходимо менять, и в рамках большого документа – это сложная и муторная задача.
Поэтому гораздо лучше в таких ситуациях описать стили в одном месте документа и затем их применять к графикам. Для создания таких пользовательских стилей известная нам команда pgfplotsset со следующими аргументами:
pgfplotsset{<style_name>/.style={<key-value-list>}};
Сразу рассмотрим пример, аналогичный тому, о котором мы говорили ранее:
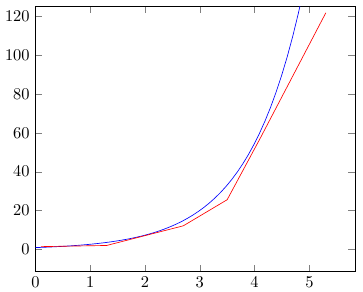
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Настройка стилей
pgfplotsset{model/.style = {blue, samples = 100}}
pgfplotsset{experiment/.style = {red}}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[xmin = 0, ymax = 125]
addplot[model]{e^(x)};
addplot[experiment] table {
x y
0.1 1.5
1.3 2.1
2.7 12.2
3.5 25.6
4.1 57.0
5.3 121.6
};
end{axis}
end{tikzpicture}
end{document}
Маркеры
Маркеры – это, если говорить в самых общих чертах, точки на графике. Ознакомится с подробным списком различных видов стандартных маркеров можно в документации (стр.160).
Как и всегда, средств для их настройки очень много, даже в документации, на которую мы ссылаемся, описаны не все из них. Рассмотрим наиболее типичные способы настройки.
Выбор типа маркера выполняется при помощи следующего свойства:
mark = <type_of_marker>
Настройка трёх основных параметров (размера, цвета заливки маркера и его контура) может быть выполнена при помощи следующего свойства:
mark options={scale = <relative_scaling>, fill = <color>, draw = <color>
Заранее предустановленных цветов очень много, но всегда можно добавить свой, например, при помощи следующей команды:
definecolor{<name_of_color}{rgb}{..., ..., ... }
Рассмотрим пример:
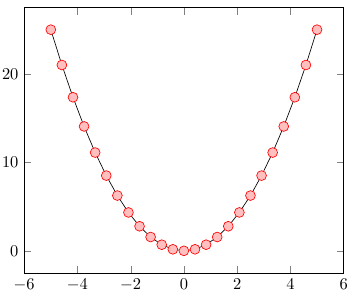
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
definecolor{chucknorris}{rgb}{192,0,0}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}
addplot[
mark = *,
mark options = {
scale = 1.5,
fill = pink,
draw = chucknorris
}
]{x^2};
end{axis}
end{tikzpicture}
end{document}
Линии графика и их цвет
Когда мы ранее говорил о чёрно-белом графике для издательства, наверняка, каждый из вас вспомнил, что одним из способов отличать один график от другого является выделение одного пунктиром, а другого сплошной линией. Всё это, естественно, можно сделать здесь.
Со всеми стилями линий (в первую очередь различными видами пунктирных линий) можно ознакомиться в документации (стр.165). Устанавливаются они при помощи указания явным образом названия стиля в опциях, например, графика.
Толщина линии графика настраивается при помощи свойства line width:
line width = <width_of_line>
Цвет линии графика настраивается при помощи свойства draw:
draw = <color>
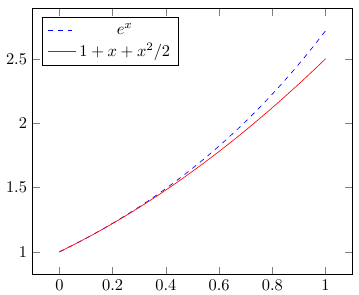
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[
domain=0:1,
legend pos = north west
]
legend{$e^x$, $1 + x + x^2/2$}
addplot[dashed, draw = blue]{e^x};
addplot[solid, draw = red]{1 + x + x^2/2};
end{axis}
end{tikzpicture}
end{document}
Примеры некоторых типов 2D-графиков
По умолчанию любой двумерный график представляет собой линейный график (для явного выбора этого типа, необходимо указать в опциях добавляемого графика свойство sharp plot). Фактически, этот тип графика просто соединяет указанные точки прямой линией. Однако на самом деле типов двухмерных графиков гораздо больше и они описаны в документации (стр.75 — 114).
Далее мы рассмотрим для примера ряд других типов графиков, которые часто приходится использовать на практике.
Гистограмма
Для создания гистограммы существуют два типа графика: горизонтальная гистограмма, которая соответствует свойству xbar, и вертикальная гистограмма, которая соответствует свойству ybar.
Ниже приведен пример создания вертикальной гистограммы, отражающей региональную структуру зачисленных на бюджетные места в 2010-2014 гг. в ВШЭ:
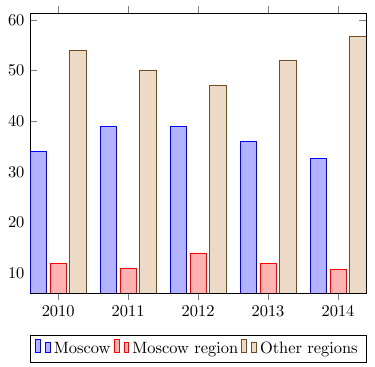
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}[
ybar,
width = 250pt,
/pgf/number format/1000 sep={},
legend style={
at={(0.5,-0.25)},
anchor=south,
legend columns=-1
}
]
addplot coordinates {
(2010, 34) (2011, 39) (2012, 39)
(2013, 36) (2014, 32.6)
};
addplot coordinates {
(2010, 12) (2011, 11) (2012, 14)
(2013, 12) (2014, 10.7)
};
addplot coordinates {
(2010, 54) (2011, 50) (2012, 47)
(2013, 52) (2014, 56.7)
};
legend{Moscow, Moscow region, Other regions}
end{axis}
end{tikzpicture}
end{document}
График рассеяния
График рассеяния – это громкое название для графика, который содержит в себе только маркеры, другими словами, он представляет собой множество точек на графике. Для выбора данного типа графика используется свойство only marks.
Рассмотрим сразу практический пример: у нас есть таблица, первые два столбца которой отражают двумерные координаты точки а третий – принадлежность к одному из трёх кластеров. Необходимо построить график, который бы отражал с одной стороны положение точек в пространстве, а с другой принадлежность их к тому или иному кластеру.
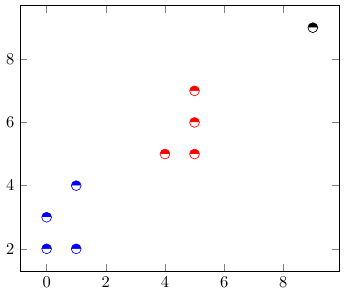
%Преамбула
documentclass{article}
usepackage{pgfplots}
pgfplotsset{compat=1.9}
%Содержимое документа
begin{document}
begin{tikzpicture}
begin{axis}
addplot[
mark=halfcircle*,
mark size=3pt,
only marks,
point meta=explicit symbolic,
scatter,
scatter/classes={
a={blue},
b={red},
c={black}
}]
table [meta=class] {
x y class
1 4 a
1 2 a
0 3 a
0 2 a
5 6 b
5 5 b
4 5 b
5 7 b
9 9 c
};
end{axis}
end{tikzpicture}
end{document}
Первое, на что стоит обратить внимание, так это на то, что в свойствах таблицы мы указываем «столбец» meta, в результате чего выбранная колонка class отвечает за некоторые мета-свойства элемента таблицы.
Затем, в параметрах указывается внешний вид маркеров, что ранее мы делали, а затем используется команда point meta, которая показывает PGFPlots, где и как ему брать мета-информацию.
point meta = none|<math_expression>|x|y|z|f(x)|explicit|explicit symbolic
Подробнее можно прочитать в документации (стр.185), остановимся лишь на том, что было выбрано значение explicit symbolic, которое означает, что мета-данные берутся из того столбца, который прописан в свойствах таблицы, причём именно как символы, а не числа.
Ну и, наконец, было указано замечательное свойство scatter, которое включает изменение внешнего вида маркеров в зависимости от их координат или принадлежности к тому или иному кластеру. В паре с ним используется свойство scatter/classes, которое задаёт то, как должен изменяться внешний вид маркера в зависимости от принадлежности к тому или иному кластеру.
Подводя итоги
Итак, статья подошла к концу, и спасибо всем, кто дочитал до сюда. Я прекрасно отдаю себе отчёт, что здесь была рассмотрена лишь вершина айсберга, лишь часть тех возможностей, которые предоставляет нам PGFPlots, и, конечно, за гранью рассмотрения осталось очень много интересных и полезных вещей. Но, надеюсь, тем не менее, статья выполнила свою задачу: познакомить и заинтересовать.
Смело высказывайте свои пожелания по тому, что вы бы хотели видеть в такой вводной статье, может быть что-то было упущено или, наоборот, где-то что-то было рассмотрено чересчур детально.
Литература и ссылки для дальнейшего изучения
 1. Основным и самым надежным источником информации по данному пакету является упоминаемая ранее массивная официальная документация.
1. Основным и самым надежным источником информации по данному пакету является упоминаемая ранее массивная официальная документация.
2. Большое количество примеров можно найти на сайте PGFPlots.net, а также здесь.
3. На большое количество вопросов, связанных с PGFPlot, ответы были получены здесь.
Автор: Norserium




