Почему PARI/GP?
PARI/GP — это система компьютерной математики с собственным C-подобным интерпретируемым языком, ориентированная на вычислительную теорию чисел. Система пользуется популярностью в научной среде: согласно Google Scholar только за 2014 год порядка 100 тематических статей, использующих PARI/GP, были опубликованы в реферируемых журналах/конференциях.
В моём диссертационном исследовании мне требовалось часто решать традиционные задачи линейной алгебры (например, для матрицы большой размерности вычислить её ядро и ранг), но только над конечными полями (например,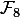 
или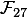 
). Если бы у нас были просто комплексные матрицы, то эффективно справились бы все хоть сколько-нибудь известные системы символьной математики: например, в любимой мною Wolfram Mathematica достаточно использовать функции NullSpace и MatrixRank соответственно. Вот было бы здорово, если эти же функции враз заработали и для матриц над конечными полями, пусть и с потерей в производительности из-за неэффективности общих алгоритмов линейной алгебры для них… Увы, я получил экспоненциальный рост (вплоть до часов на моём бедном нетоповом ноутбуке) времени вычислений от размерности матриц (см. мой вопрос на профильном форуме по Wolfram Mathematica). Правда, справедливости ради, это было вызвано не столько проблемами реализации алгоритмов линейной алгебры, сколько проблемами самого процессора символьных вычислений.
К моей великой радости PARI/GP предназачается именно для расчётов в различных алгебраических системах (кольцах, полях), оперируя их элементами как «атомарными» числами, а не как символьными структурами над встроенными типами. По моему эмпирическому наблюдению, PARI/GP имеет непревзойдённую скорость таких вычислений. К тому же есть возможность трансляции интерпретируемого кода в чистый C.
Основные функции для работы в конечных полях
Описание далее достаточно «высокоуровневое», без отсылки к алгоритмам и структурам данных, используемым внутри PARI/GP (темы будущих постов).
- Функция ffinit(q, n, {v}) вычисляет нормированный неприводимый над простым полем
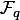многочлен f(v) степени n от переменной v (необязательный параметр, по умолчанию многочлен будет от аргумента x). Например: вызов ffinit(2, 3, x) вернёт примитивный многочлен 
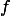, а ffinit(2, 4, x) — уже просто неприводимый многочлен 
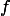. Теперь мы можем задать расширение 
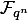конечного поля 
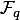классически, как фактор-кольцо 
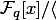. - Корень
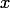неприводимого многочлена f(x) как объект PARI/GP создается при помощи функции ffgen(f, x). Другими словами, вызов g = ffgen(f, x) возвращает объект g, отождествлённый с классом эквивалентности [x] — элементом фактор-кольца 
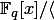. Теперь поле 
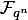, рассматриваемое как линейное пространство над 
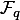, можно построить (его таблицы сложения и умножения) с помощью порождающего множества 
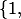. - Найти примитивный элемент поля можно с помощью функции ffprimroot(g). Эта функция вычисляет случайный элемент порядка (n — 1) в мультипликативной группе конечного поля, которое задано объектом g.
- С помощью функции minpoly(a) можно найти минимальный многочлен элемента a конечного поля. Например, вызов p = minpoly(a) вернет
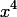. Другими словами, найдя примитивный элемент поля 
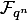, поле можно представить в традиционном виде 
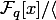, где p — его примитивный многочлен.
Жизненный пример
Предварительная справка
Как было уже сказано, PARI/GP использует свой C-подобный язык. Подробное руководство можно посмотреть тут. Далее следует небольшое описание, поясняющее отдельные моменты примера ниже (и даже больше):
- Все объекты в PARI/GP создаются на его внутреннем стеке. По умолчанию, внутренний стек занимает 3.8Мб (4 миллиона байт) динамической памяти компьютера. Чтобы его расширить, используется функция allocatemem(s), где s — это запрашиваемое количество байт
- Разделитель ";" в конце строки используется для запрета вывода результата на печать.
- По умолчанию, любой идентификатор является переменной для многочленов. Можно использовать перед идентификатором апостроф, который указывает, что перед нами именно переменная для многочленов, а не какой-то объект. Например,
x = 12; type(x) >"t_INT" type('x) >"t_POL" - Фигурные скобки "{", "}" используются только для группировки команд (например, многострочных). Группировка не задаёт область видимости (жизни) любого объекта, объявленного внутри неё. По умолчанию, все объявленные переменные — глобальные. Чтобы объект стал локально связанным, его надо объявить с использованием спецификатора my. Например,
{ x = 12; } x >12 { my(y = -13.2); } y >y - PARI/GP позволяет пользователю создавать лямбда-функции. Синтаксис следующий: lambda = (список аргументов) -> тело функции;
Сам пример
createField = (q, n, var) -> ffgen(minpoly(ffprimroot(ffgen(ffinit(q, n, var), var))), var);
a = createField(2, 4, 'x)
>x
fforder(a) \ вычисляет мулььтипликативный порядок элемента
>15
allocatemem(2^27); \ аллоцирует 128Мб памяти под внутренний стек PARI/GP
M = matrix(1000, 1000, i,j, random(a)); \ создает случайную 1000х1000 матрицу над полем GF(16)
{gettime(); matrank(M); gettime()} \ вернет время (мс) на расчёт ранга этой матрицы
>34209
{gettime(); kernel(M~); gettime()} \ время на расчёт ядра пространства строк этой матрицы
>88425
Конфигурация моего ноутбука — Intel® Core(TM) i7-4702M CPU @ 2.20GHz 2.20GHz, 32kB L1 cache, 8Gb DDR3. Использовался PARI/GP 2.7.2 (32bit, single thread) — это последний на момент публикации этого текста релиз, «работающий из коробки» под ОС Windows.
Автор: semenovp
