Hello.
Недавно, так уж вышло, читал в своем старом лицее лекцию на тему того, зачем они учат математику и что с ней можно потом делать чуть более прикладного. Для школьников 10-го класса оказалось чуть сложновато, пожалуй. Надеюсь данная тема будет интересно кому нибудь из хабрасообщества (здесь представлен вариант чуть-чуть сложнее того, что я читал в лицее, но не думаю, что это проблема).
Итак. Речь пойдет об обработке изображений, в частности об одном из самых простых, однако красивом с описательной точки зрения, методе подавления шумов в изображении.
Не так давно я для себя открыл сколько физики заключается в обработке изображений. Меня это очень заинтересовало, в виду того, что эти две ветви науки у меня в голове никогда не пересекались. В этой статье я представлю как можно убрать шумы с изображения решая задачу переноса массы на плоскости.
Представление изображения
Сначала уточним, что будем считать изображением. Для простоты описания мы будем рассматривать сейчас только ч/б изобрежения.
Представлять их будем как матрицу насыщености.

Таким образом каждому пикселю изображения соответствует элемент матрицы. Значения в матрице — числа типа float из промежутка [0,255].
Возьмем какое нибудь изображение и добавим к нему шум (это проще, чем искать изображение уже с шумом, так как можно проверить на сколько алгоритм хорошо справляется с шумами, задавая разную интенсивность шума). Получим нечто такое:

Изображение как функция
Для дальнейшего объяснения метода, мне нужно ввести кое-какие обозначения:
Во-первых, далее мы будем рассматривать наше изображение как функцию от координат пикселей. Таким образом, если мы хотим сказать, что пиксель с координатами х и у белый, то мы можем записать это как I(x,y)==255
Далее, если у нас есть функция, то мы можем взять от нее производную и далее нам это пригодится. Так как функция у нас дискретная, то есть задана в ячейках, с установленным шагом между ними, то мы можем ее записать как (так как функция двумерная, то и производных, соответсвенно две):
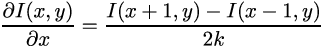
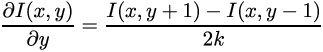
Тут k==1 так как разница между соседними пикселями = 1 пиксель.
Таким образом, производные будут тоже матрицами такого же размера как и исходное изображение:


Имея производные по обеим координатам логично посчитать градиент:
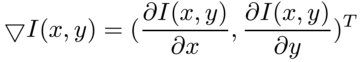
И его величину:
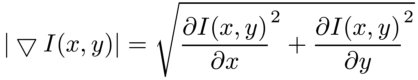
Величину градиента можно вывести в виде изображения:

Теперь, внимательно посмотрим на величину градиента. Она имеет большие значения там, где хранится нужная нам информация.
Чтобы избавить изображение от шума логично, что его нужно размыть. Однако при размытии теряются важные детали. То есть мы хотели бы ограничить размытие в зонах, где градиент достаточно большой. Оставлся только вопрос как это сделать.
Связь с процессом диффузии
Здесь нам на помощь приходит замечательный физический процесс диффузии. Представим матрицу изображения как индикатор наличия массы в той или иной точке плоскости. Процесс диффузии заключается в том, что масса «растекается» из точек с большой ее концетрацией в точки с малой. В процессе диффузии присутствует понятие потока, который подчиняется так называемому закону Фика:
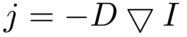
Где D — Тензор диффузии, который задает направление и величину диффузии.
Запишем так же закон сохранения массы, который говорит о том, что разница входящего и исходящего потоков равна изменению массы в точке:
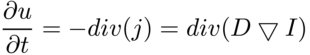
Если поток не ограничивать, то есть D==1 — масса будет распространяться во всех направлениях равномерно, то есть мы получим эквивалент Гауссовского размытия, а значит потеряем важные детали изображения. Нас интересует метод, с помощью которого поток можно ограничивать.
Одним из самых простых методов является ограничение величины потока, не ограничивая его направления. Про него и будем говорить далее.
Введем в рассмотрение некоторую убывающую функцию, на вход которой будем подавать величину градиента. Эта функция на данном этапе будет представлять собой тензор диффузии:
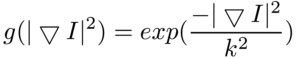
Тогда уравнение сохранения массы принимает вид:
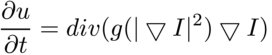
Далее распишем все формулы (этот шаг я, пожалуй, опущу) и запишем конечное уравнение, с помощью которого можно найти решение задачи:
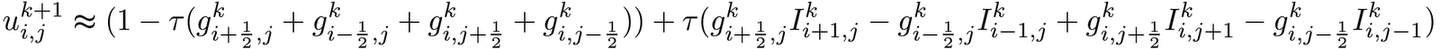
Таким образом мы получили итерационную схему, которая стабильна при значениях параметра tau<=0.25. Она довольна медленна, так как метод базовый и более успешные алгоритмы базируются на нем.
Результат
В конце концов мы получим изображение, которое сохранило почти все важные детали и лишилось почти всего шума.

Для сравнения — оригинал и версия с шумом (еще раз):


Литература:
- P. Perona, J. Malik: Scale-space and edge detection using anisotropic diffusion. IEEE
Transactions on Pattern Analysis and Machine Intelligence 12(7):629-639, 1990. - J. Weickert: Anisotropic Diffusion in Image Processing. Teubner, Stuttgart, 1998. The book is
not available anymore, but the PhD thesis of Joachim Weickert, which was the basis of his
book, is available on his website. - T. Brox: Lectures on Computer Vision. Freiburg im Breisgau, 2011
P.S. При обнаружении неточностей — буду рад услышать критику и пожелания.
Автор: niosus



