Во многих случаях задачи, решаемые в электродинамике, сводятся к разделению переменных и прогонке на суперкомпьютере «подогнанных» конечных разностей, но, боюсь, что «жесткость» уравнений Максвелла просто «сдирает» точность вычислений настолько, что их нельзя использовать даже для оценки. Далее приводятся элементарные преобразования уравнений Максвелла и в итоге схема упрощающая вычисления/описание поля, но к сожалению, не объем.
(Тема сугубо техническая, касается только вопросов обработки данных расчетов электродинамики, много формул.)

Далее используются только CGS единицы, для перевода в SI за основу можно взять Материал из Википедии «Уравнения Максвелла»
Набивая эту статью, столкнулся с первой неожиданкой (для затравки...) микроскопической системы уравнений
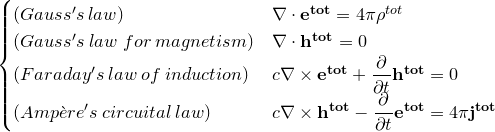
сведутся к «уравнению непрерывности» 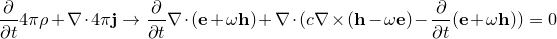
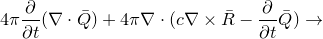
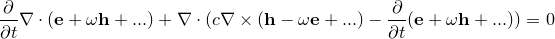
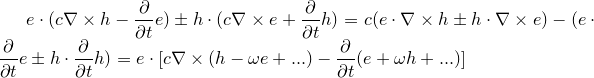
«Первая часть мырлизонского балета»
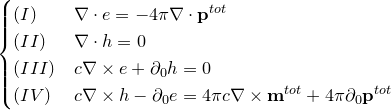
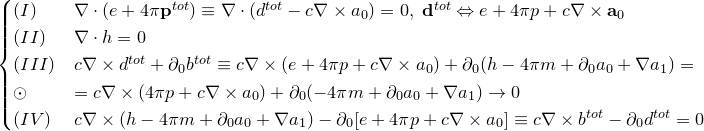
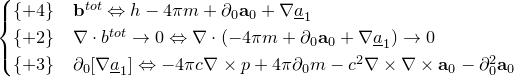
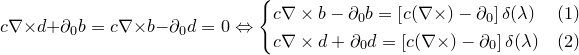
![]()
«Вторая часть мырлизонского балета» The MÚNERA — GUZMÁN — Ansatz
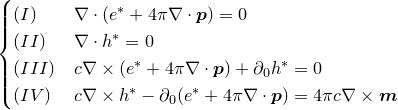
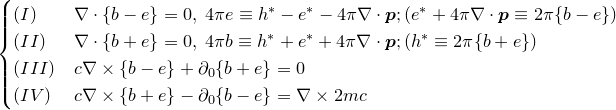
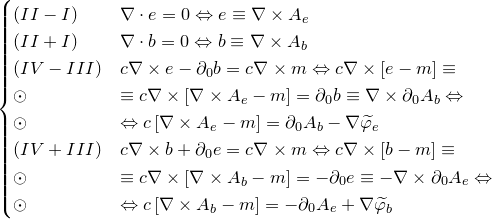
[en] André Waser On the Notation of MAXWELL’s Field Equations
«Третья часть мырлизонского балета»
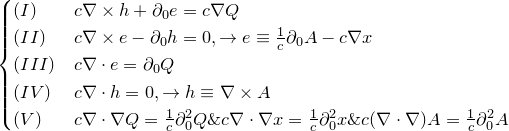
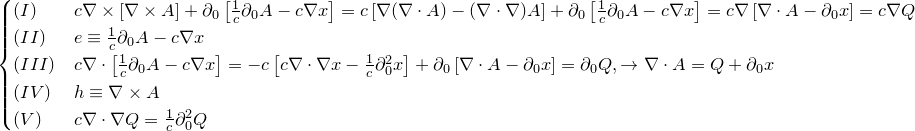
Тут дефект почти не заметен, но… Найдете?
В системе с лоренцевой калибровкой или такой, все равно исходят из градиента, а при j=qv даже шанса нет построить непротиворечивую систему (ну кто построит скорость из керла?). Привет КЭДу!
«до Апофеоз»
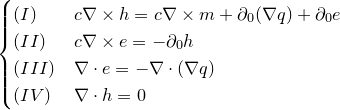
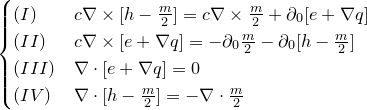
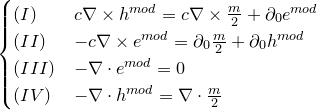
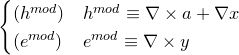
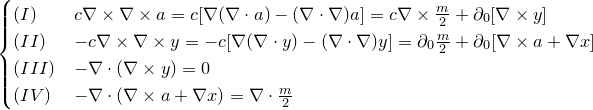
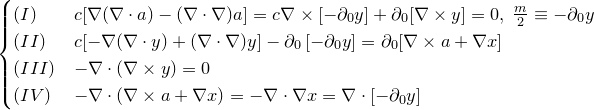
«xfiles»
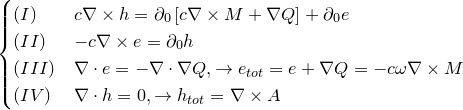
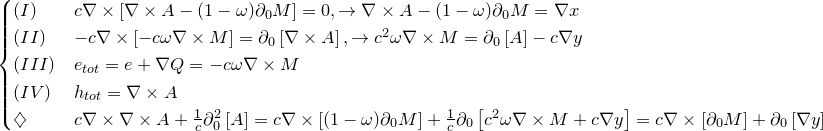
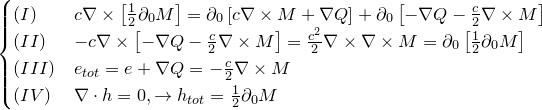
Сила Лоренца: 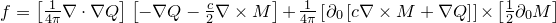
Вектор Пойнтинга: 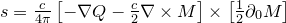
Ради выражения силовых функций через единое поле все это и затевалось. Электродинамика — ТФКП в чистом виде, см. учебник 1958 года «Лаврентьев М.А., Шабат Б.В. Методы теории функции комплексного переменного» глава III глава «Плоское поле и комплексный потенциал», вопрос в том, где делать талию логарифм.
Начнем с простого вопроса: «где существует это поле?»
— Ньютонианское поле строится на «световом конусе», проходящее через датчик (для построения «тока» требуется согласования нескольких, в идеале — поверхности(датчик в фокусе параболы?), что и является самой сложной операцией), на нем нет времени, фотонов и «близкодействия».
Время?
— Поля(не поле) на световом конусе не пересекаются, элементарные частицы сохраняют суммы зарядов, от начала времен, и до конца (да нужно знать, что было, и что будет, да плохая бесконечность). Движение волн можно аппроксимировать полиномами Ньютона.
Элементарные частицы?
— Логарифмическая особенность соответствующего логарифма аппроксимированного полиномом поля, если протон считать двигающимся в будущее, то и все положительные частицы туда, отрицательные — в прошлое, а нейтральные — интерференция партонов. [en] шпасибо Лукмору за ссылку
Полином?
— Состоящий из произведений ( R-Rk ), Rk — координата частицы относительно датчика, на конусе. После чего сминаем пространство в пространство-время: ( t — ( R-Rk )/c ) +- ( t + ( R-Rk )/c )i — для положительных, а ( t + ( R-Rk )/c ) +- ( t — ( R-Rk )/c )i — для отрицательных. Фейнман, как-то, помянул, что электроны похожи друг на друга потому, что они в своей сути один и тот-же электрон. Как, и за то спасибо Фейнману, что вернул обратную волну в электродинамику.
Автор: Duduka