Данная работа описывает способы сжатия прежде всего социальных(графы связей между пользователями в социальных сетях) и Web-графов(графы ссылок между сайтами).
Большинство алгоритмов на графах хорошо изучены и спроектированы из расчета того, что возможен произвольный доступ к элементам графа, на данный момент размеры социальных графов превосходят RAM среднестатистической машины по размеру, но в тоже время легко умещаются на жестком диске. Компромисным вариантом являтся сжатие данных с возможностью быстрого доступа к ним определенных запросов. Мы сконцентрируемся на двух:
а) получить список ребер для определенной вершины
б) узнать соединяются ли 2 вершины.
Современные алгоритмы позволяют ужимать данные до 1-5 бит на ссылку, что делает возможным работу с подобной базой на среднестатистической машине. Меня сподвигло написать данную статью именно желание уместить базу друзей vkontakte в 32GB оперативной памяти, что с учетом того что сейчас там порядка 300M аккаунтов со средней степенью вершины около 100 представляется вполне реалистичным. Именно на данной базе я буду проводить свои эксперименты.
Общими свойствами интересующих нас графов является
а) то что они большие, 1е6 — 1е9 и более верхин и порядка 1е9 ребер — что делает невозможным работу с ними напрямую в памяти, но позволяет без проблем хранить их даже на одном жестком диске. На сайте law.di.unimi.it/datasets.php представлен весь обширный спектр подобных баз.
б) рапредление степеней(degree) вершин, да и вообще все важные частотые характеристики описывается степенной зависимостью(Power-Law) как минимум асимптотически.
в) они разреженные. Средняя степень вершины ~ 100-1000.
г) вершины похожи — вероятность того что у вас общий друг в больше для связаных вершин.
Boldi и Vigna.
В данной работе граф в «естественном», несжатом виде будет представлятся массивом списков:
node1 -> link11,link12,link13...
node2 -> link21,link22,link23....
....
Где link[i,j] < link[i,j+1].
| Вершина | Степень вершины | Ребра |
|---|---|---|
| 15 | 11 | 13,15,16,17,18,19,23,24,203,315,1034 |
| 16 | 10 | 15,16,17,22,23,24,315,316,317,3041 |
| 17 | 0 | |
| 18 | 5 | 13,15,16,17,50 |
Таблица 1. Естественное кодирование графа. (Пример взят из работы [2])
Назовем разницу между индексами двух ссылок «гэпом».
Gap[i,j] = link[i,j-1] - link[i,j] Первой из семей алгоритмов компрессии являются методы, использующие следущие 2 основных подхода:
а) Эксплуатация локальности вершин. Вершины чаще ссылаются на «близкие» вершины, нежели на «дальние».
б) Эксплуатация похожести вершин. «Близкие» вершины ссылаются на одни и те же вершины.
В этих двух утверждениях кроется парадокс — термин «близости» вершин можно описать так же через похожесть, тогда наши утверждения превратятся в трюизм. Именно в разъяснении понятия «близости» и есть основное отличие между опробованными мной алгоритмами.
Первая работа на эту тему это повидимому K. Randall [1]. В ней был исследован веб-граф еще здравствующей Altavista, и было обнаружено что большинство ссылок ( 80% ) на графе локальные и имеют большое количество общих ссылок и было предложено использовать следущее референтное кодирование:
— новая вершина кодируется как ссылка на «похожую» + список добавлений и удалений, который в свою очередь кодируется гэпами + nibble coding.
Ребята сжали альтависту до 5бит за ссылку ( я буду стараться приводить наихудшие результаты сжатия в работах ). Данный подход получил большое развитие в работах Paolo Boldi и Sebastiano Vigna.
Ими был предложен более сложный метод референтного кодирования, представленный в таблице 2. Каждая вершина может иметь одну ссылку на «похожую», RefNr кодирует разность между текущей вершиной и ней, если RefNr равен нулю значит вершина не имеет ссылки. Copy list представляет из себя бит-лист, который кодирует какие вершины необходимо забрать по ссылке — если соответствующий бит Copy list равен 1, то данная вершина так же принадлежит и кодируемой. Потом Copylist так же кодируется RLE подобным алгоритмом и превращается в CopyBlocks:
01110011010 -> 0,0,2,1,1,0,0
Мы записываем длинну — 1 для каждого повторяющегося блока + значение первого блока ( 1 или 0 ), а оставшиеся в конце нули можно отбросить.
Остаток вершин преобразуется в гэпы, отдельно кодирются интервалы нулей (тут эксплуатируется особое свойство веб-графов, речь о котором пойдет ниже) а остальные гэпы(Residuals) записываются кодировнными одним из цифровых кодов (Golomb,Elias Gamma и как экстремум Huffman).
Как видно из таблицы 2, данное кодирование может быть многоуровневым — степень этой многоуровневости является одним из параметром кодировщика L, при большом L скорость кодировки а также раскодирования падает, но степень компрессии, увеличивается.
| Вершина | Степень вершины | RefNr | количество copy-блоков | Copy blocks | Количество интервалов | интервалы(относительный левый индекс) | длинны интервалов | остаток(Residual) |
|---|---|---|---|---|---|---|---|---|
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 15 | 11 | 0 | 2 | 0,2 | 3,0 | 5,189,11,718 | ||
| 16 | 10 | 1 | 7 | 0,0,2,1,1,0,0 | 1 | 600 | 0 | 12,3018 |
| 17 | 0 | |||||||
| 18 | 5 | 3 | 1 | 4 | 0 | 50 | ||
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
Таблица 2. Способ референтного кодирования, предложенного Boldi и Vigna для данных из таблицы 1. [2]
Распределение Гэпов в базах краулеров так же подчиняется Power-Law закону.
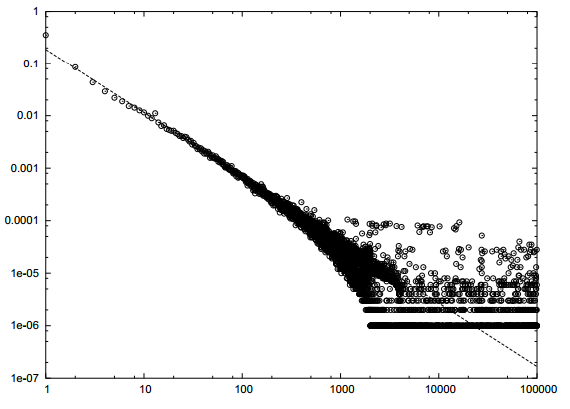
Рисунок 1. Распределение «Гэпов» в снапшоте по .uk сайтам — 18.5М страниц.
Что позволило сказать «близкие» аккаунты даны нам свыше в виде упорядоченных данных от вебкраулеров. И далее уже развивать работу по указанным выше двум направлениям: кодировать список ребер как модификацию одной из предыдущей вершины (референтное кодирование), хранить список ребер в виде «Гэпов» ( Gap[i,0] = Node[i] — link[i,0] ) — и, используя частотную характеристику, выявленную выше — кодировать данный список одним из многочисленных целочисленных кодов. Надо сказать, что получилось у них неплохо: 2-5 bit на ссылку [4]. В [2] и [3] предложены даже более простые методы референтного кодирования LM и SSL которые кодируют данные небольшими блоками. Результат превосходит или скорее соизмерим с BV алгоритмом. От себя хочу добавить, что даже простое кодирование гэпами дает соизмеримый результат на Web — базах и одновременно все методы использующие локальную «похожесть» заметно пасуют на социальных базах.
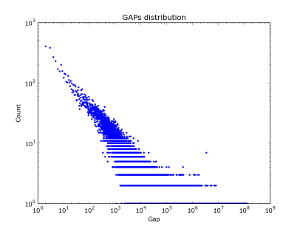
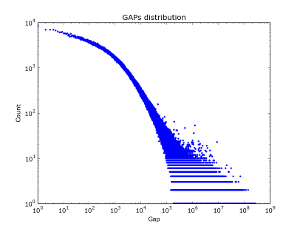
В социальных графах — данный эфект, похоже не наблюдается — на рисунке 2 представлено распределения гэпов по разным кускам базы данных vkontakte. Интересно что для первого миллиона аккаунтов log/log закон для Гэпов на самом деле выполняется. Но с увеличением количества данных. Распределение гэпов становится все более и более «белым».
|
|
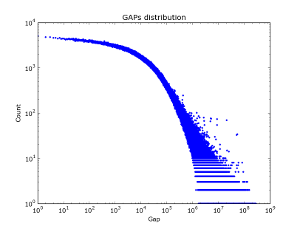
|
| Выборка 50к. | Выборка 100к. | Выборка 2М. |
Рисунок 2. Распределение гэпов по базе друзей vkontakte.
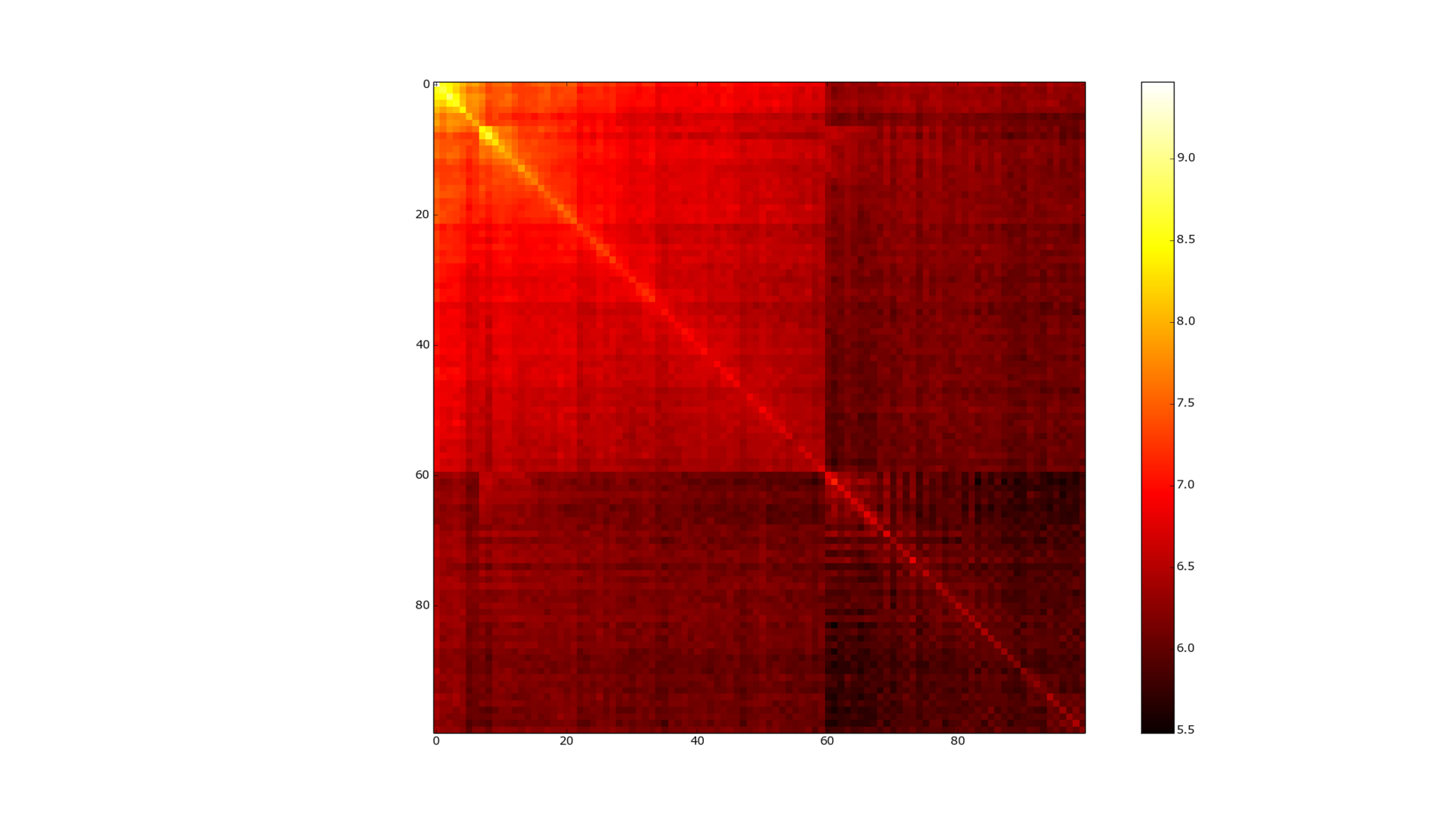
Рисунок 3. Матрица смежности графа, vkontakte.
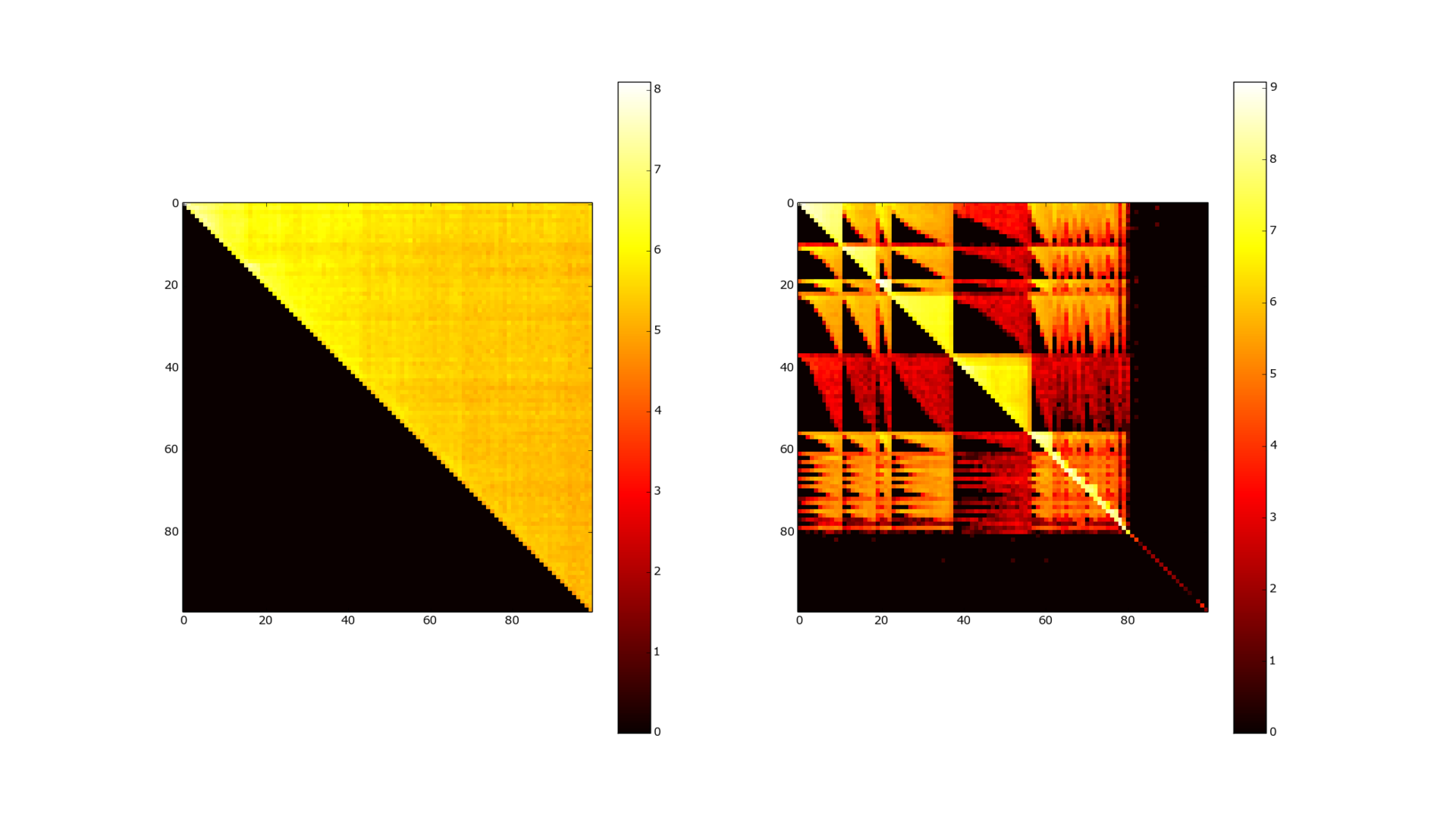
Рисунок 4. Матрица смежности до и после кластеризации. 100к пользователей.
На рисунке 3 предтавлена матрица смежности графа друзей, в логарифмическом виде. Она тоже не внушает особых надежд на компрессию такого рода. Гораздо интереснее выглядят данные, если каким либо образом предварительно кластеризовать наш граф. Рисунок 4 показывает матрицу смежности после прохода MCL ( Markov Cluster Algorithm) кластеризатора. Матрица соответствия становится почти диагональной (карта цветов логарифмическая, поэтому яркий желтый означает на несколько порядков большее количество связей между элементами) — и для компрессии таких данных уже отлично подходит и WebGraph и многие другие алгоритмы. (Asano [7] — на данный момент являющийся самым лучшим насколько мне известно по компрессии но и самым медленным по доступу к данным).
Но проблема в том, что MCL в худшем случае кубичен по времени и квадратичен по памяти (http://micans.org/mcl/man/mclfaq.html#howfast). В жизни все не так плохо для симметричных графов ( каким социальный граф почти является ) — но до линейности ему всеравно далеко. Еще большую проблему составляет то, что граф не умещается в памяти и надо придумывать распределенные техники кластеризации — а это уже совсем другая история. Промежуточное решение данной проблемы придумали Alberto Apostolico и Guido Drovandi [1] — перенумерацию графа, просто проходя по нему поиском в ширину (BFS-search). Таким образом гарантируется, что некоторая часть ссылающихся друг на друга вершин будет иметь близкие индексы. В своей работе они ушли от GAP кодирования и заменили его на достаточно сложную модель ссылочного кодирования, получив при этом 1-3 бит на кодируемую ссылку. На самом деле не очень ясна интуиция по которой BFS должен правильно компоновать вершины, но данный метод работает — я проделал данное кодирование для вконтактовской базы и посмотрел хистограмму по гэпам (Рисунок 5) — она выглядит очень многообещающе. Есть так же предложения, использовать Deep First Search вместо BFS, а так же более сложные схемы переиндексации например shingle reordering [7] — они дают схожий прирост. Есть еще один довод, почему BFS переиндексация должна/может работать — WebArchive базы хорошо кодируются, а они получены как раз последовательной индексацией живого интернет графа.
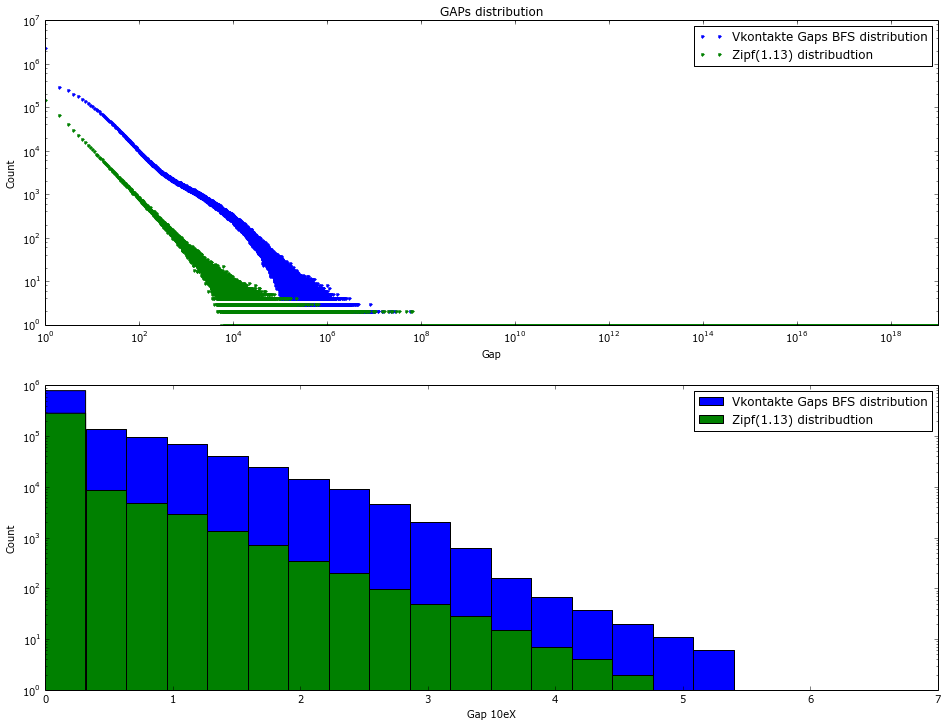
Рисунок 5. Распределение гэпов по базе друзей vkontakte после BFS индексации. 100k выборка
| Gap | Количество | Доля |
|---|---|---|
| 1 | 83812263 | 7.69% |
| 2 | 12872795 | 1.18% |
| 3 | 10643810 | 0.98% |
| 4 | 9097025 | 0.83% |
| 5 | 7938058 | 0.73% |
| 6 | 7032620 | 0.65% |
| 7 | 6322451 | 0.58% |
| 8 | 5733866 | 0.53% |
| 9 | 5230160 | 0.48% |
| 10 | 4837242 | 0.44% |
| top10 | 153520290 | 14.09% |
Таблица 2. Распределение гэпов по базе друзей vkontakte после BFS индексации. 1M выборка
Вторая работа Boldi и Vigna [5] посвящена теоретическому обоснованию кодирования списка гэпов различными цифровыми кодами а так же сравнение их с Хафмман кодированием как возможным upper bound. За основу берется то, что кодируемая величина распределена по закону Ципфа. Верхняя граница сжатия для различных параметров альфа получилась у них 4-13 бит на ссылку. Для базы вконтакте данный способ кодирования дал 18 бит на ссылку. Что конечно, уже не плохо и позволяет уместить всю базу в RAMе, но очень далеко от терретических оценок, приводимых в работах. На рисунке 5 показано сравнение распределения гэпов после BFS индексации, с распределением ципфа, максимально близким к практическим данным ( альфа = 1.15). На рисунке 6 показана матрица смежности для графа после BFS переиндексации — она хорошо отображает причину плохого сжатия — диагональ прочерчена хорошо но общий шум еще очень велик по сравнению с кластеризованой матрицой. Данные «плохие» результаты также подтверждаются работой [6].
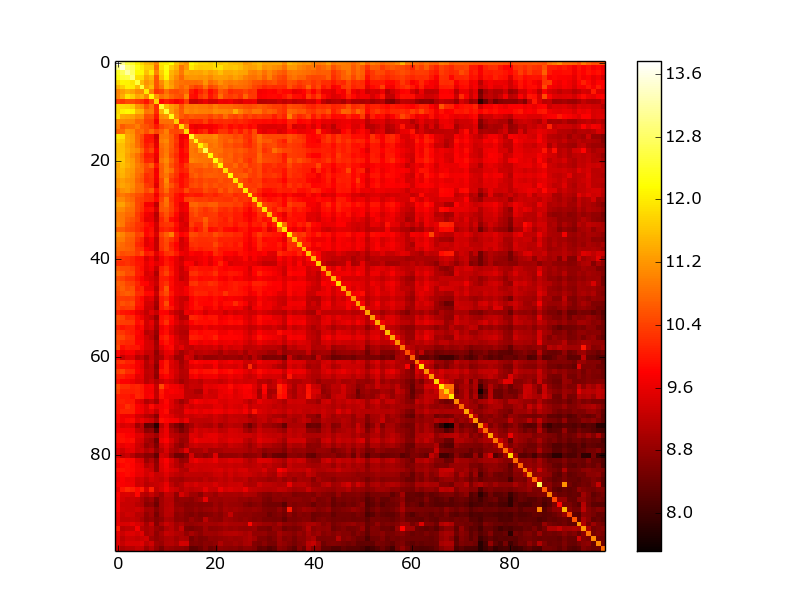
Рисунок 6. Матрица смежности базы vkontakte. После BFS переиндексирования.
Биклики
Есть еще один, заслуживающий отдельного внимания метод — эксплуатация свойств графа. А именно выделение биклик (Bipartite graph) и генерация виртуальной вершины соединяющей 2 части подграфа. Это позволяет уменьшить длинну списков вершин для каждой стороны двудольного графа. Данная задача в общем случае NP-полная но существует множество хороших эвристик для нахождения двудольных подграфов. Данный метод предложен в [9], как и BV алгоритм породил множество других[10-11] и заслуживает более детального рассмотрения. На рисунке 6 описана лишь основная его идея.
 |
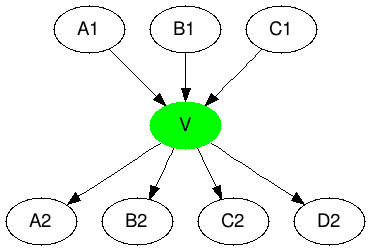 |
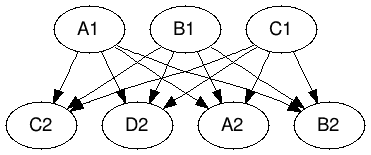
| А1 -> А2 B2 C2 D3 B1 -> А2 B2 C2 D4 C1 -> А2 B2 C2 D5 |
А1 -> V D3 B1 -> V D4 C1 -> V D5 V -> A2 B2 C2 |
Рисунок 6. Кодирование бикликами.
- A. Alberto and G. Drovandi: Graph compression by BFS.
- Sz. Grabowski and W. Bieniecki: Tight and simple Web graph compression.
- Sz. Grabowski and W. Bieniecki Merging adjacency lists for efficient Web graph compression
- P. Boldi and S. Vigna: The webgraph framework I: Compression techniques.
- P. Boldi and S. Vigna: The webgraph framework II: Codes for the World-Wide-Web. WebGraphII.pdf
- P. Boldi and S. Vigna. Permuting Web and Social Graphs.
- Flavio Chierichetti, Ravi Kumar. On Compressing Social Networks.
- Y. Asano, Y. Miyawaki, and T. Nishizeki: Efficient compression of web graphs.
- Gregory Buehrer, Kumar Chellapilla. A Scalable Pattern Mining Approach to Web Graph Compression with Communities
- Cecilia Hernandez, Gonzalo Navarro. Compressed Representations for Web and Social Graphs.
- F. Claude and G. Navarro: Fast and compact web graph representations.
Автор: marten_de