Мало кто задумывается, что те приемы, которые мы используем для письма и счета формировались на протяжении многих тысяч лет. Нам они кажутся очевидными, ну, подумаешь, умножить в столбик, перенести все члены с неизвестным на одну сторону. Ведь это так просто! На самом деле это огромные интеллектуальные завоевания человечества, которые часто были недоступны умнейшим людям прошлого. Я собираюсь (если хватит терпения и времени) написать несколько заметок о том, как считали в прошлом. В этой я расскажу про то, как считали египтяне.
Меня всегда немного интересовал древний Египет. Ну, во-первых, Египет — одно из первых государств, о котором мы много знаем, и кроме того, это очень великое государство, которое оставило огромное наследие. Я не имею в виду огромные размеры пирамид. Даже наша письменность и латинская, и кириллическая восходит к древнему Египту. Мне также всегда нравилась египетская скульптура, и мода брить голову у женщин и мужчин. Это кажется очень современным. Но это статья не о художественной культуре. Так что приступим.
Цифры и числа
Египтяне пользовались непозиционной десятичной системой счисления. Выглядели цифры примерно так:

Эти цифры относятся к т.н. иероглифическому письму, которое позже было заменено иератическим. Я очень люблю иератическое письмо. Оно выглядит весьма стильно. Но здесь я буду использовать иероглифическое начертание.
Все целые числ образовывались путем повторения знаков, приведенных выше (и некоторых других для еще более высоких разрядов). Например, 3215 будет:

Очень ясная система, хотя не слишком лаконичная. Ее просто освоить, но числа получаются не слишком удобными. С первого взгляда трудно уловить точное значение числа. Писали египтяне в разных направлениях, но я здесь пишу как привычно нам слева на право.
Теперь насчет дробей. Для трех дробей существовали специальные значки:
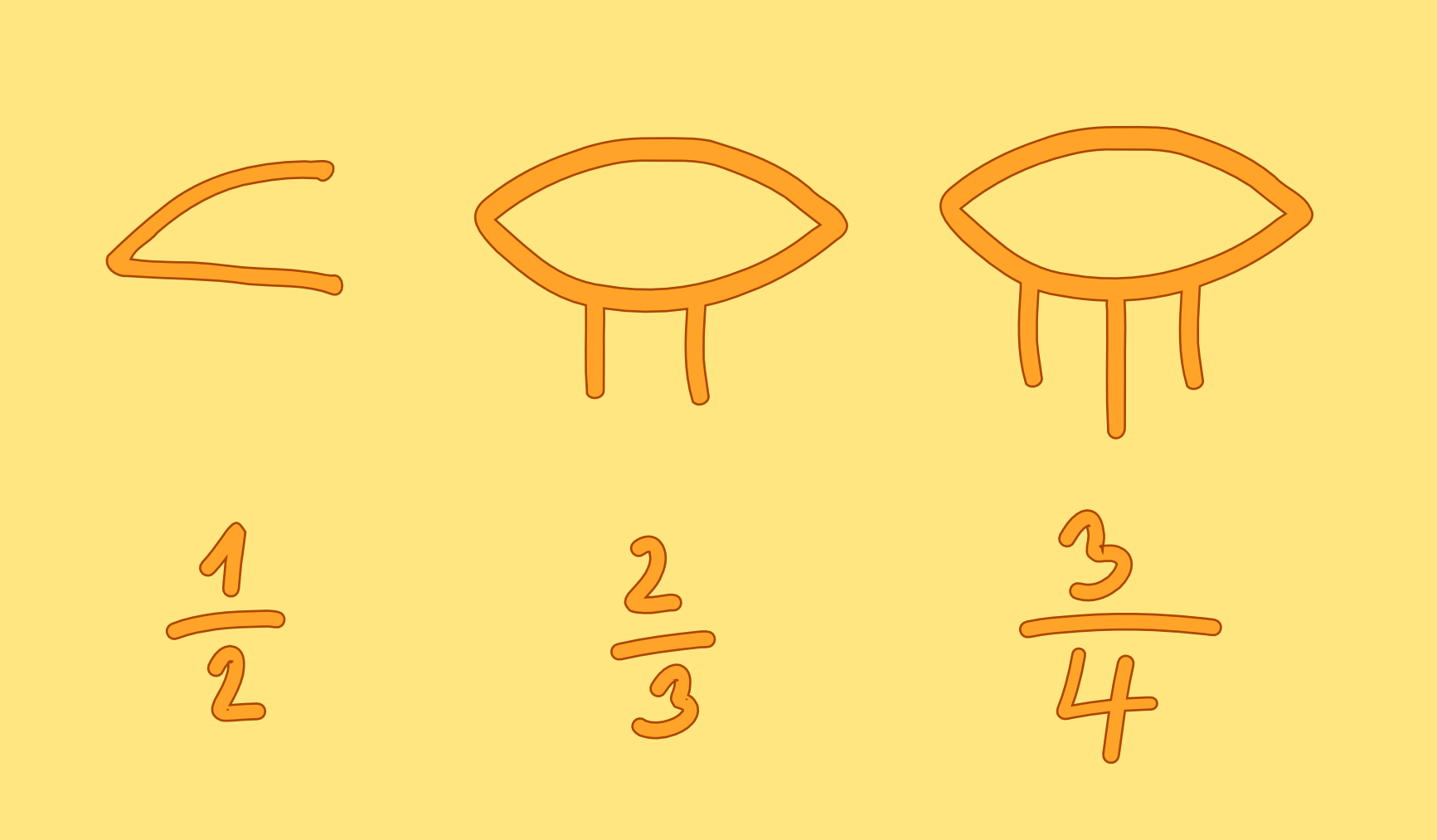
Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху. Например, ниже я написал 1/14

Все правильные дроби записывались как сумма таких дробей. Например:

На одном сайте я прочитал, что «в некоторых случаях» египетские дроби «лучше наших». И даже в английской вики, есть такой чудный пример: «Египетские дроби иногда легче позволяют сравнить размер дробей. Например, если некто хочет знать, больше ли 4/5, чем ¾ он может превратить их в египетские дроби:
4/5= 1/2 + 1/4+ 1/20
3/4= 1/2 +1/4»
Мне этот «легкий способ» напоминает шутку про Фейнмана, который ради какой-то задачи школьного курса просуммировал ряды в уме. Я гуманитарий и особо не умею считать, но сравнивать в уме обычные дроби в их нормальной записи мне кажется гораздо проще, чем переводить их в египетский вид. Возможно, для египтян сравнения такого рода и были более удобны, так как наших дробей они не знали.
Сложение и умножение
Ну, вот мы и переходим к главному. Как египтяне считали? Сложение и вычитание целых чисел у них происходило также как и у нас, а может быть даже проще, им ведь просто нужно было объединить иероглифы и учесть смену разрядов. А как обстоит дело с умножением и делением? В древнеегипетском мире это была вовсе не тривиальная задача.
Египтяне использовали такой алгоритм для умножения. В два столбца писались числа. Первый столбец начинался с единицы, а второй с множимого. Затем каждое число в столбце удваивалось до тех пор, пока из некоторых чисел первого столбца не удастся сложить множитель. Вы поняли? На примере понятно лучше. Например, 7 на 22
| 1 | 22 |
| 2 | 44 |
| 4 | 88 |
8 уже больше, чем 7, поэтому табличка заканчивается на четырех. Теперь 1+2+4=7 значит 22+44+88=154. Хотите верьте, хотите нет но 154 это верный ответ. Конечно в египетской записи (я не знаю, как она точно выглядела) такие вычисления были проще, ведь умножать на 2 в египетской записи очень просто.
Еще пример, немного сложнее: 13 умножить на 57
| 1* | 57 |
| 2 | 114 |
| 4* | 228 |
| 8* | 456 |
1+4+8=13 и 57+228+456=741
Иногда, чтобы ускорить процесс прибегали к умножению на 10.
Может возникнуть вопрос, всегда ли можно представить множитель в таком виде? Да, на самом деле мы фактически имеем дело с двоичной системой счисления: 1*20+0*21+1*22+1*23 т.е. 1+100+ 1000=1101
Деление выполнялось при помощи схожего алгоритма. Разделим 238 на 17:
Опять составляем табличку с одной стороны, которой стоит 17 с другой единица. Процесс удвоения останавливается на числе, которое при удвоении будет больше делимого.
| 1 | 17 |
| 2 | 34 |
| 4 | 68 |
| 8 | 136 |
Здесь нужно составить число 238 из чисел второго столбца, начиная с конца. 136+68+34=238, значит нам нужны числа 8+4+2=14. Итак, 238/17 =14
К несчастью, деление не всегда приводит к целому числу. В ряде случаев это было довольно сложно. Я покажу простой пример, заимствованный мной из одной книги.
Разделим 213 на 8
Сначала все, как обычно.
| 1 | 8 |
| 2* | 16 |
| 4 | 32 |
| 8* | 64 |
| 16* | 128 |
Здесь мы останавливемся, ведь 128 на 2 = 256, а это больше 213. 128+64<213. 128+64+32 уже опять больше. Не подходит. 128+64+16<213 Пока все ОК. 128+64+16+8 уже больше. Значит мы смогли набрать только 208=128+64+16 из 213. И нам осталось разделить 213-208=5
Мы делим делитель по полам, используя уже привычную таблицу. К счастью 5 это 1+4.
| 1/2* | 4 |
| 1/4 | 2 |
| 1/8* | 1 |
Таким образом, окончательный результат будет
213/8 = 2+8+16+1/2+1/8 =26+1/2+1/8
Сейчас мы имеем удачный случай, но так получается не всегда.
Автор: Sychuan

