
В теории вероятностей и статистике правило первой цифры, или закон Бенфорда, показывает любопытное проявления частот первой цифры данных из реальной жизни. Для школьников и домохозяек этот закон можно вольно сформулировать так: есть наборы данных, у которых первая цифра будет единицей примерно в 6 раз чаще, чем девятка и это соотношение не изменится при масштабировании исходного набора. Более строго можно сформулировать так: набор чисел удовлетворяет закону Бенфорда, если первая цифра d появляется с вероятностью
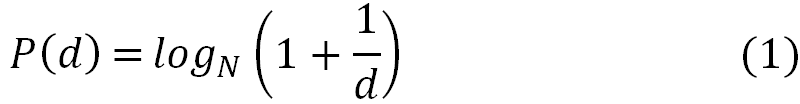
Здесь N – основание системы счисления, должно быть больше 2, далее будем рассматривать 10.
Для строгих математиков это правило формулируется так: существуют такие случайные величины, для которых распределение вероятностей дробной части логарифма по любому основанию большему 1 сходится к равномерному на отрезке [0; 1] распределению. Далее я постараюсь писать как можно популярнее и подробнее, укажу примеры, ограничения, применение и случайные величины, для которых закон применим.
Начнем с классического примера. Рассмотрим список стран по населению, например, с википедии . Получим таблицу частот для первой цифры, это можно сделать прямо открыв консоль в википедии:
var populationList = $('table.sortable tr').map(function () {return $('td:nth-child(3)', this).text()}).toArray();
var frequency = [undefined, 0, 0, 0, 0, 0, 0, 0, 0, 0];
var countriesCount = populationList.length;
$(populationList).each(function () { frequency[this[0]] += 1 / countriesCount });
Теперь можно сопоставить получившиеся частоты, с частотами закона Бенфорда, рассчитанных по формуле (1):
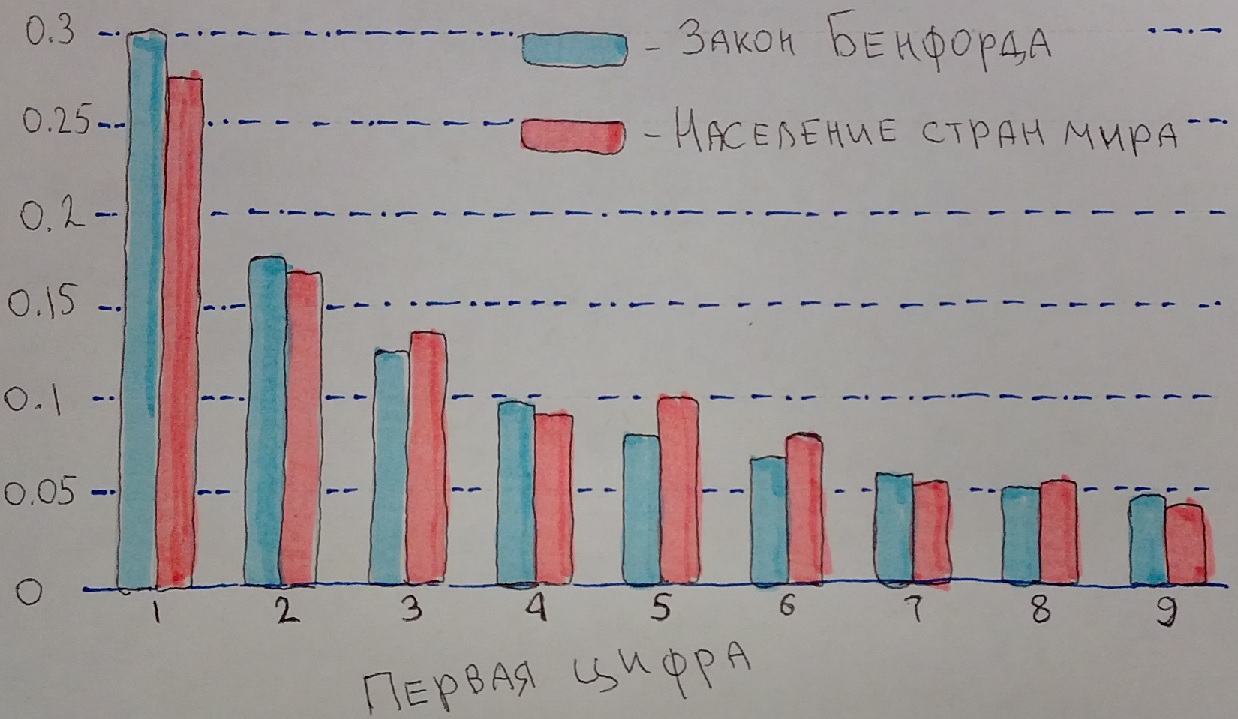
Посмотреть и поиграться, подставляя свои данные можно здесь jsfiddle.net/Vr3F9/.
Далее рассмотрим еще несколько данных из реальной жизни: население городов России, список стран по количеству заключённых и рейтинг пользователей с сайта dev.by dev.by/users.
Здесь я приведу только результаты, как их получить, вы уже знаете. Откройте, пожалуйста, и не закрывайте диаграмму jsfiddle.net/rWbBs/, я ее сейчас объясню. На изображении видно, что все распределения имеют много общего с законом Бенфорда, и только список стран по количеству заключенных имеет некоторые несоответствия с законом, но все равно похож на него больше, чем, скажем, на равномерный закон распределения. В данных из реальной жизни именно так и случается, что помимо распределений, хорошо соответствующих закону, есть такие, которые остаются «похожими» на него, даже при достаточно большом увеличении числа наблюдений, про математическую часть этого вопроса еще будет сказано, пока просто запомните как факт.
Теперь зададимся вопросом, какие наблюдаемые значения из реальной жизни удовлетворяют закону Бенфорда. Вот список некоторых из них.
1. Население стран и городов. Как следствие: результаты демографических измерений, результаты выборов, региональные показатели, пропорциональные населению.
2. Площади бассейнов рек, площади стран и территорий, размеры островов.
3. Тиражи газет и книг.
4. Повседневные расходы. Просто посмотрите на все свои покупки за какой-то период времени.
5. Показатели изменений на финансовых рынках (отдельная большая тема, уверен что, кто-то из вас знает ее лучше меня).
Теперь самое время рассказать про законы, не попадающие под закон Бенфорда. Под этот закон не попадают сильно популярные равномерные и нормальные распределения. Также попадаются распределения с часто встречаемой первой единицей и на первый взгляд, похожих на закон Бенфорда, например атомная масса элементов и основные физические константы. Про атомную массу элементов хочется сказать особенно. Сам Бенфорд в оригинальной статье, изображение заголовка которой я сделал КДПВ , указывал атомную массу, как пример закона удовлетворяющего «правилу первой цифры», однако закону, описываемому формулой (1) это распределение не удовлетворяет, хоть и видно явное преобладание первой единицы. И вот как легко в этом убедиться: достаточно умножить все значения на какое-нибудь одинаковое число, и посмотреть, что будет.
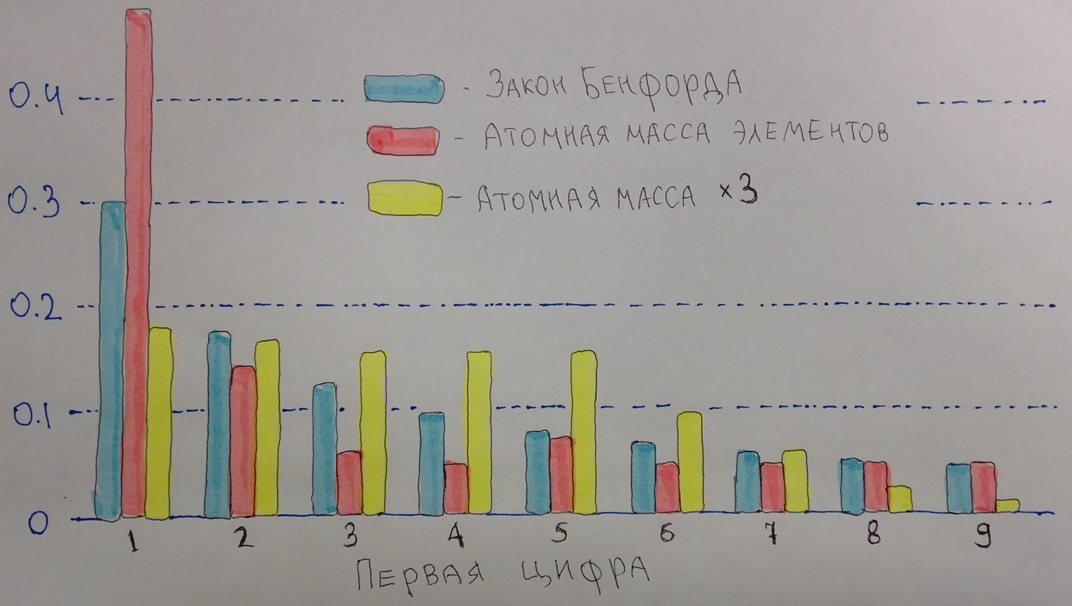
Закон Бенфорда масштабируем: при умножении всех наблюдаемых значений на одно и то же число, он продолжает выполняться, с атомной массой видно, что это не так.
Перейдем к математическим объектам, удовлетворяющих закону. Вот небольшой список:
1. Последовательность степеней двойки, и любая другая экспоненциальная последовательность.
2. Числа Фибоначчи.
3. Факториалы.
Также есть два распределения из курса Теории вероятностей, подчиняемых данному закону. Первое это гамма-распределение, при k→0 это распределение подчиняется закону (см ссылку на статью mi.mathnet.ru/tvp113). Я не встречал случаев, чтобы на практике приходилось работать с этим распределением со столь малым параметром.
А вот второй класс распределений интереснее. Оказывается, что к закону Бенфорда сходятся односторонние устойчивые распределения (ссылка на статью: mi.mathnet.ru/tvp244). Про устойчивые распределения я писал в своей предыдущей статье. Напомню кратко, что это такое. Здесь, возможно, будет немного сложно, можете сразу читать следующий абзац, основную мысль ввы не потеряете. Есть класс распределений, удовлетворяющий обобщенной центральной предельной теореме, то есть эти распределения с точностью до масштаба и сдвига сохраняют свой вид при суммировании. Вот именно это свойство сохранять вид функции распределения и называется устойчивостью. Этих распределений целый класс, описываемый четырьмя параметрами, два из которых это сдвиг и масштаб как в нормальном распределении, третий параметр асимметрии, а четвертый самый важный параметр альфа, принимающий значения от нуля до двух характеризует, степень «тяжести хвоста» распределения. При альфа равном двум устойчивое распределение будет нормальным, это частный, и даже можно сказать вырожденный случай, так как только в этом случае распределение будет иметь моменты любого порядка, во всех остальных случаях моменты будут только порядка меньше альфы. То есть, дисперсия будет бесконечна, ну статистически ее можно посчитать и получить какое-то значение, но оно для разных выборок из одного и того же распределения будет принимать сильно разные значения. А при альфа меньшем, или равном единице, не будет и математического ожидания. То есть наши рассуждения «в среднем» для этого случая просто бессмысленны. И вот как раз для случая очень маленьких альф и в случае односторонности (принимают только положительные или отрицательные значения, этого можно добиться при правильном выборе параметра асимметрии), эти распределения и удовлетворяют закону Бенфорда.
Что общего можно сказать про односторонние устойчивые распределения с малым параметром хвоста, удовлетворяющих закону Бенфорда: они все не имеют среднего значения и одновершинные, статистически это можно объяснить так: существует небольшой по сравнению с разницей максимального и минимального значения, где будет находиться большинство значений. Чем больше мы проводим наблюдений, тем больше вероятность получить еще более аномальное значение. Так вот с примером про список стран по количеству заключенных: там просто параметр альфа не так сильно устремлен к нулю, а значит будет просто похожесть на закон Бенфорда, а не строгое ему соответствие, даже при весьма значительном увеличении числа наблюдений. Теперь можете закрыть этот пример, скоро вас ожидает более интересный.
Сейчас попробую пояснить, что распределений, не имеющих среднее значение в реальной жизни, гораздо больше, чем может показаться. Представьте, что вы гуляете с маленьким ребенком, возможно даже своим, по лесу. И он показывает на сосну и спрашивает: «а это дерево высокое?». Ответ на этот вопрос прост: если оно выше среднего, значит высокое, а если не совсем, то не совсем. Среднюю высоту сосны можно узнать. А вот дальше, этот же самый ребенок показывает вам камень и спрашивает: «а этот камень большой?». Теперь согласитесь, размер среднего камня для каждого человека будет свой и вероятность наткнуться на камень размером на порядки больше привычного не так уж мала.
А вот теперь более наш пример такого распределения. Размер файла на носителе. Попробуйте сходу ответить на вопрос, какой средний размер файла на вашем системном диске? Догадались? Зайдите в какую-нибудь папку, желательно имеющую побольше файлов и на системном диске, а не там, где собраны однотипные вещи вроде фоток и музыки. Теперь выведите список всех файлов и посмотрите, какая часть размеров из них начинается с единицы, двойки и так далее. Готов спорить, что девятка будет гораздо реже двойки (просто я уже много где успел проверить и даже убедился в устойчивости этого распределения). Такая же ситуация будет и с размером таблиц и числом записей в таблице в базе данных. Устойчивость и как следствие «тяжелый хвост» в этом случае означает, что две-три самые большие таблицы в базе данных будут занимать больше места, чем все остальные вместе.
Основное применение закона Бенфорда: определение возможной фальсификации входящих значений в случаях, когда значения должны удовлетворять этому закону: в сетях передачи данных, с системах хранения данных, при проведении социалогических опросов и выборов, некоторых научных экспериментах и так далее. Также закон Бенфорда чем-то похож и даже связан с принципом Парето и законом Ципфа, но это уже отдельные темы, так что будет продолжение…
Автор: paunch







Спасибо за интересный материал.