Однажды тихой летней ночью по ходу решения насущных аналитических задач встал вопрос о том, как же следует измерять степень вариативности поисковой выдачи? В поисках ответа удалось обнаружить одно-единственное исследование на эту тему – Кокшаров, 2012.
Но удовлетворения не получил, вопросов стало ещё больше. Использование алгоритмов Оливера и Левенштейна только потому, что соответствующие функции есть в PHP, показалось необоснованным. А обоснования методов, базирующихся на разнице позиций, – неубедительными.
Почему так, а не этак? Почему массив или строка, а не упорядоченное множество или кортеж? К чему могут привести сделанные допущения? И, наконец, существует ли один-единственный самый лучший, самый правильный, самый «окончательный» способ?
В результате пришлось изобретать свой собственный велосипед – то есть расставить всё по полочкам хотя бы для себя. Но всё-таки с надеждой, что это будет интересно будет не только мне.
Мера вариативности рейтинга
Поиск готового математического аппарата также ничего не дал. Упорядоченное множество? Строка? Массив?… Всё не то. Самое близкое – кортеж/вектор, но используемые там меры расстояний не отражают сути рейтинга. Либо я чего-то не знаю, либо слишком много лет прошло со студенческих времён. Надеюсь, те, кто чаще упражняется с математикой, меня поправят или хотя бы натолкнут на мысль, в какой стороне искать. Мы же пока попробуем ввести собственные определения, оставаясь в терминах предметной области.
Для обозначения всеми любимых Топ3, Топ10, Топ100 и т.д. введём понятие «рейтинг N» как упорядоченную последовательность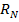 
длины 
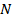, содержащую идентификаторы ранжируемых объектов
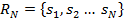, (1)
где под идентификатором объекта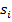 
будем понимать ссылку (URL) на ранжируемый документ.
Самое простое и естественное предположение состоит в том, что мера вариативности должна быть как-то связана с изменением позиций объектов в рейтингах. Чем больше разница (расстояние) между новой и старой позицией конкретного объекта и чем больше объектов, изменивших свою позицию, – тем больше должна быть и разница между двумя рейтингами.
В такой постановке расстоянием между двумя рейтингами будем называть сумму разниц позиций всех объектов, входящих в рейтинги. Попробуем выразить это определение более формально.
Пусть даны два рейтинга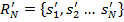 
и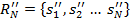 
. Элементы этих рейтингов могут совпадать полностью или частично, а могут и полностью не совпадать.
Тогда пусть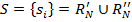 
– множество объектов, входящих в оба сравниваемых рейтинга. Мощность 
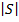этого множества (количество входящих в него элементов) будет варьироваться от 
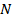(в случае, когда объекты в обоих рейтингах полностью совпадают и различие между рейтингами состоит только в их перестановке) до 
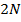(в случае, когда элементы двух рейтингов полностью различаются).
Один и тот же объект может находиться в рейтингах как на разных позициях, так и на совпадающих. А может вообще отсутствовать в одном из рейтингов.
Назовём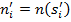 
позицией 
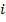-го объекта в рейтинге 
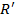, а 
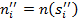– позицию этого же объекта в рейтинге 
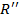. Тогда расстоянием между позициями 
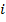-го объекта будет модуль их разницы
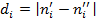(2)
Просуммировав разницы в позициях по каждому элементу множества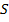 
получим следующее выражение для расстояния между двумя рейтингами в абсолютных величинах:
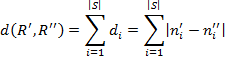(3)
Нет проблем вычислить данное расстояние, когда объекты присутствуют в обоих рейтингах. Но что делать, когда в одном из рейтингов отсутствуют объекты другого рейтинга, то есть находятся за его пределами? В этом случае представляется весьма обоснованным принять за позицию отсутствующего объекта значение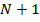 
– ближайшую позицию, находящуюся за пределами рейтинга.
Понятно, что в реальной жизни сайт может вылететь, например, из Топ10 намного дальше 11-го места. И можно повышать точность оценки вариативности поисковой выдачи, рассматривая рейтинги бόльшей длины – 30, 50, 100, 1000. Весьма вероятно, что при больших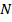 
это допущение будет играть всё меньшую роль. Пока же вопрос о выборе оптимальной длины рейтинга остаётся открытым и нам остаётся довольствоваться утверждением, что оценки вариативности, полученные с данным допущением будут оценками минимальной разницы в том смысле, что расстояние между рейтингами будет не меньше полученной оценки.
Оценки абсолютной разницы между рейтингами трудны для интерпретации и сравнения. Для удобства оперирования оценками их следует привести к относительной форме. В качестве нормировочного значения нам потребуется найти максимально возможное расстояние между рейтингами. Понятно, что оно будет соответствовать случаю, когда рейтинги полностью различаются по составу элементов. То есть все объекты рейтинга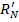 
оказались за его пределами, а все объекты рейтинга 
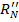появились из-за его пределов. То есть каждый объект рейтинга 
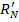переместился со своей позиции на на позицию 
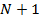, а каждый объект рейтинга 
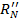, наоборот, переместился с позиции 
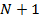на свою позицию.
Тогда для рейтинга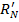 
максимально возможной суммой расстояний будет:
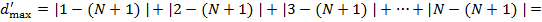
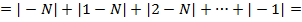
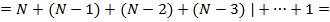
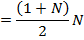
То есть мы получили сумму арифметической прогрессии с первым членом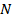 
, шагом -1, и последним членом 1.
Соответственно, для второго рейтинга, когда каждый его объект переместился с позиции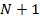 
на свою позицию, мы получим подобную арифметическую прогрессию с первым элементом 1, шагом 1 и последним элементом 
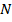, сумма которой 
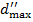будет определяться таким же выражением.
В итоге получаем, что суммарное расстояние, на которое переместились объекты первого и второго рейтинга, будет определяться выражением
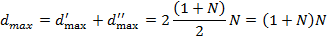(4)
Значит, для относительной оценки вариативности рейтинга получаем следующее выражение
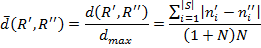(5)
Желающие могут разобраться с этим более подробно на небольшом примере.
, 
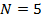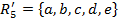, а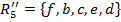 
.Тогда
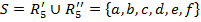
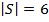
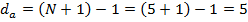
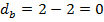
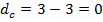
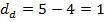
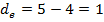
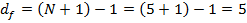
Отсюда абсолютное расстояние между рейтингами будет
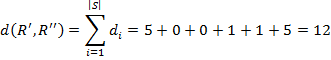
Максимально возможное расстояние будет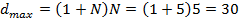 
.
Значит, получим следующее относительное расстояние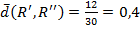 
или 40%
Взвешенная мера вариативности рейтинга
Внимательный читатель может заметить, что оценки степени изменения рейтинга, полученные по выражениям (3) или (5) слабо чувствительны к локальным изменениям вообще и к транспозициям в частности. (Транспозиция — это когда два элемента просто меняются местами). Если поменяются местами два первых элемента или два последних, мы получим одну и ту же разницу. Например, транспозиция 1-го и 2-го места или 4-го и 5-го даёт одну и ту же разницу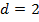 
.
Возможно с точки зрения поисковика и его функции ранжирования такие изменения действительно несущественны. Но меня, как практикующего маркетолога, интересуют в первую очередь последствия для подопечных сайтов. А вот последствия эти, даже в случае локальных изменений, могут быть весьма существенны. И связано это в первую очередь с тем, что кликабельность поисковой выдачи сильно зависит от занимаемого места в рейтинге (в serp’е) и, следовательно, достаточно сильно (в разы) меняется и органический трафик, получаемый сайтами, находящимся в области локальных изменений.
Таким образом, желательно было бы учитывать тот факт, что разница между 1-м и 2-местом в поисковой выдаче намного больше, чем разница между 4-м и 5-м. Для этого нам нужно ввести весовую функцию для мест в рейтинге. И лучшей такой функцией, отражающей изменение поискового трафика, будет зависимость кликабельности поисковой выдачи от занимаемой позиции.
Вообще, выбор «хорошей» аппроксимирующей функции для статистики кликабельности serp’а — это тема для отдельного исследования. В идеале она зависит от очень большого количества параметров: поисковой системы, типа ключевого слова, качества сниппета, состава сайтов, наконец. Но для наших целей, когда нас интересуют не столько абсолютные, сколько относительные (разница мест) оценки, можно воспользоваться практически любой из известных. Мне привычнее пользоваться следующей зависимостью, приведенной в Самуйлов, 2014, которая демонстрирует достаточно хорошие аппроксимирующие возможности
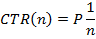, (6)
где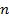 
– позиция в рейтинге, 
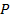– параметр, зависящий от поисковой системы и принимающий значения: 
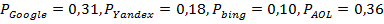. Усреднённое значение 
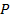по всем поисковым системам 
.
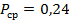С учётом (6) расстояние между позициями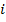 
-го объекта примет вид
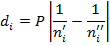(7)
А абсолютное расстояния между рейтингами, соответственно, будет
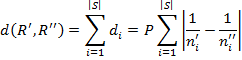(8)
Максимально возможное взвешенное расстояние между рейтингами будет определяться выражением
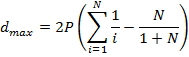(9)
Тогда взвешенное относительное расстояние будет определяться выражением
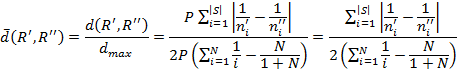(10)
Следует обратить внимание, что в итоге взвешенное относительное расстояние на зависит от параметра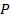 
, то есть от поисковой системы.
Для приведённого выше примера взвешенное расстояние составит 61%. То есть оно чувствительнее к замене лидера рейтинга.
Ну и существенно чувствительнее к локальным изменениям: транспозиция 1-2 в рейтинге Топ5 будет иметь значение 34%, а транспозиция 4-5 – значение 3,4%.
Вариативность профильных рейтингов
Полученные меры можно использовать для разных задач анализа флюктуаций поисковой выдачи. Этими задачами определяются конкретные профили для анализа: состав поисковых запросов (по типу, тематике, длине, частотности), область поиска (по региону, веб/новости/иллюстрации/блоги) и т.п.
Анализ апдейтов поисковых систем. Это уже стало классической задачей анализа вариативности поисковой выдачи. Чем представительнее набор ключевых слов, тем лучше будет оценка глобальных изменений алгоритма/базы ранжирования.
Задачи управления репутацией. В качестве набора ключевых слов здесь используются брендовые запросы, относящиеся к вашей компании/продукции. Анализируя флюктуации новостной выдачи можно определять повышенную активность в интересующем вас профиле.
Анализ конкуренции в нише. Повышенное разнообразие поисковой выдачи по тематическим запросам можно интерпретировать как показатель низкой конкуренции, когда однозначные лидеры ещё не определились.
В качестве заключения
Как же определить, какой способ анализа вариативности поисковой выдачи является «самым окончательным»? Можно называть свои методы «правильными» апдейтами, «точными», «самыми точными»… Но сколько не говори «халва» — во рту слаще не станет.
Единственный вариант — это сравнительный анализ различных методов на исторических выборках и оценка их чувствительности к уже известным фактам изменения функций ранжирования поисковиков. К сожалению, у меня нет такой статистики. Но был бы рад поработать вместе с теми, у кого она есть.
Автор: NetMozg
