Пост написан под влиянием поста пользователя pchelintsev_an.
В данной статье я постараюсь рассказать, с какими вычислительными трудностями можно столкнуться, если пойти по «наивному» пути вычисления матричной экспоненты. Статья может быть полезна тем, кто хотел бы познакомиться с вычислительной математикой. Эксперименты проводились с использованием системы GNU Octave.
Что вообще такое матричная экспонента и кому она нужна
Матричная экспонента возникает при рассмотрении задачи Коши для линейной системы обыкновенных дифференциальных уравнений с постоянными коэффициентами:
Иногда такие системы возникают после частичной дискретизации уравнений в частных производных, например, в методах конечных элементов. Тогда матрица A является некоторой конечномерной аппроксимацией дифференциального оператора. Как следствие, число строк матрицы A может легко достигать тысяч, миллионов и даже нескольких миллиардов. Такие матрицы даже невозможно хранить в виде квадратного массива, поэтому их хранят в специальных разреженных форматах представления.
Решение системы ОДУ можно выписать явно:
Здесь появляется матричная экспонента, которая определяется как сумма ряда:
Фактически, матричная экспонента получается формальной подстановкой матрицы A в ряд Тейлора для ez(Математик отметит, что ряд сходится абсолютно для любой матрицы и любого t). Удобно то, что с помощью матричной экспоненты можно вычислить решение в любой момент времени t. Например, если эту систему решать каким-нибудь методом численного интегрирования, например, Адамса или Рунге-Кутты, то затраченное время будет пропорционально времени t. Однако, решение через матричную экспоненту возможно лишь для автономных систем с постоянными коэффициентами.
В курсе дифференциальных уравнений для практических вычислений матричной экспоненты предлагается метод приведения матрицы к жордановой форме: если матрицу A представить в виде S J S-1, где J – жоржанова форма, S – матрица перехода к жорданову базису, то матричная экспонента А выражается через матричную экспоненту J:
Матричная экспонента от жордановой матрицы J выписывается в явном виде. Однако такой способ требует вычисления системы собственных векторов, а также присоединенных к ним векторов. Эта задача значительно сложнее исходной. К тому же, даже для действительной матрицы А, ее жорданова форма J может быть комплексной.
Суммирование ряда
Итак, у нас есть бесконечный ряд и желание вычислить его за обозримое время. Очевидный путь – закончить суммирование на каком-то слагаемом, отбросив остаток. При этом суммирование ряда заканчивается, если очередное k-е слагаемое по норме мало:
Нормы матрицы
Остановимся ненадолго на норме матрицы. Различных норм матрицы существует достаточно много. Можно ввести норму, исходя из требования
В этом случае говорят о норме матрицы индуцированной (или подчиненной) некоторой векторной норме. Для наиболее употребимых векторных норм соответствующие матричные нормы имеют вид:
Первые две нормы матрицы считаются элементарно, а для последней требуется вычислить сингулярное число, что весьма непросто. Кроме индуцированных норм существует еще ряд других норм. Практически удобной является норма Фробениуса, которая, с одной стороны, легко вычисляется, а с другой – тесно связана с сингулярными числами А. Фактически, это евклидова норма вектора, полученного «вытягиванием» матрицы в одну строку:
Сюрпризы при суммировании ряда
Чтобы осознать сложности, возникающие при суммировании рядов Тейлора, не обязательно обращаться к примеру с матричной экспонентой. Попробуем просто построить график функции e-x на отрезке [0, 50], суммируя аналогичным образом ряд Тейлора для экспоненты. Суммирование завершим, если очередное слагаемое не превосходит 10-20. Воспользуемся следующим кодом на Octave:
function [y] = myexp(x, eps)
xk = ones(size(x));
y = xk;
k = 0;
do
k = k + 1;
xk = xk .* x / k;
y = y + xk;
until (max(abs(xk)) < eps)
end
x = linspace(0, 50, 2000);
y = myexp(-x, 1e-20);
plot(x, y, 'b', x, exp(-x), 'r');
axis([0 50 -0.1 1.1]);
Результат получается довольно странным:
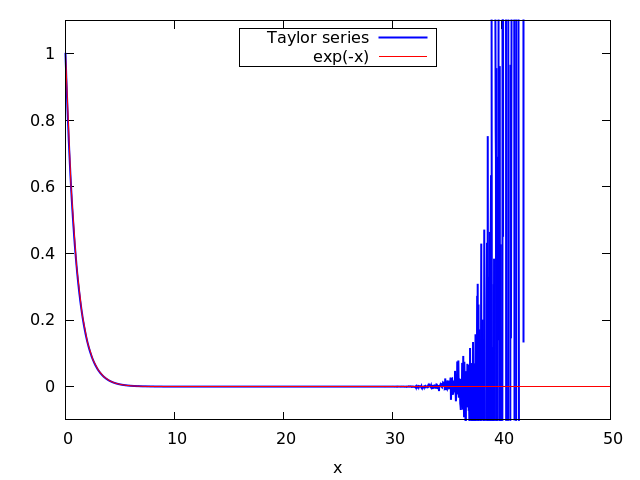
При x > 30 график функции начинает вести себя хаотично и не имеет с экспонентой ничего общего.
Причина данного эффекта в накоплении погрешностей округления. Например, при вычислении e-35 было просуммировано 132 слагаемых, из которых минимум абсолютной величины имело последнее слагаемое s132 ≈ 5.8674 · 10-21, а максимум абсолютной величины имело слагаемое с номером 35: s35 ≈ -1.067 · 1014. Поскольку Octave проводит вычисления с двойной точностью (примерно 16 значащих цифр), округление 35-го слагаемого уже внесло ошибку порядка 0.01, что существенно превосходит и значение ϵ = 10-20 и само значение суммы ряда e-35 ≈ 6.305 · 10-16
Неужели ряд Тейлора настолько безнадежен? Нет, ошибки округления не будут давать существенного вклада, если величина суммируемых слагаемых не будет достигать таких огромных значений. Например, такой алгоритм будет надежно работать при небольших значениях x (|x| ≲ 1). Для матричной экспоненты аналогичное условие имеет вид . Кроме вычислительной устойчивости такой выбор x обеспечивает быструю сходимость, то есть достаточно взять всего несколько слагаемых из ряда для получения приемлемой точности.
Метод удвоения аргумента
Заметим, что матричная экспонента удовлетворяет следующему соотношению:
Это означает, что матричную экспоненту можно посчитать для матрицы , а затем возвести результат в степень N. Взяв в качестве N = 2p можно воспользоваться быстрым алгоритмом возведения в степень за p матричных умножений:
- Вычислить матричную экспоненту
- Умножить B на себя , повторив эту операцию p раз
- В результате,
Число p можно (и нужно) выбрать из соображений вычислительной устойчивости шага 1 алгоритма, то есть
Соответствующий Octave код:
function [B] = taylorexp(t, A, eps, max_terms)
B = eye(size(A));
Ak = B;
k = 0;
while norm(Ak, 'fro') > eps && k < max_terms
k = k + 1;
Ak = (t / k) * Ak * A;
B = B + Ak;
end
end
function [B] = argdbl(t, A, eps, max_terms)
p = ceil(log2(abs(t) * norm(A, 'fro')));
B = taylorexp(t / pow2(p), A, eps, max_terms);
for i = 1:p
B = B * B;
end;
end
Метод аппроксимаций Паде
Отрезок ряда Тейлора – не единственный способ приближенно вычислить значение функции. Более качественные приближения функции могут быть получены не в виде многочленов, а в виде рациональных функций. Наилучшие приближения в виде отношения двух многочленов заданных степеней называются аппроксимациями Паде. Например, аппроксимация Паде отношением двух квадратичных многочленов для экспоненты записывается в виде:
Аналогичная аппроксимация для матричной экспоненты будет иметь вид:
Аппроксимации Паде могут использоваться для шага 1 в алгоритме удвоения. Основная сложность, связанная с аппроксимациями Паде, заключается в необходимости один раз обратить матрицу. Для больших матриц это может быть довольно трудозатратно.
Анализ точности
Как убедиться, что матричная экспонента вычислена правильно? Достаточно ли, что или требуется более «интеллектуальная» проверка?
Вспомним, что матричная экспонента возникла не на ровном месте, а в результате решения некоторой системы обыкновенных дифференциальных уравнений. Собственные числа матрицы A характеризуют скорости процессов, протекающих в системе, описываемой данной системой дифференциальных уравнений. Например, матрица:
описывает систему с одним быстро затухающим процессом (собственное значение -1000) и двумя колебательными процессами (собственные значения ±i). Хорошим критерием правильности вычисления матричной экспоненты может являться соотношение:
связывающее собственные значения матрицы A и ее матричной экспоненты.
Вычислительный эксперимент
Для начала исследуем алгоритмы на быстродействие на случайных матрицах разного размера. В качестве методов используем метод суммирования ряда Тейлора, метод удвоения аргумента и встроенную в Octave функцию expm. Изначально хотелось сравнить также соответствие собственных значений, но от этой идеи пришлось отказаться, поскольку все три алгоритма одинаково проваливали эту проверку при размерах матрицы N ≳ 50. Возможно виновником этого была функция определения собственных значений eig, работающая недостаточно точно или плохая обусловленность самой задачи определения собственных значений для этих матриц.
Исходя из графика, метод удвоения работает примерно вдвое дольше библиотечной функции (возможно стоит ослабить завышенное требование по точности), в то время как прямое суммирование имеет даже иную асимптотику ≈O(N3.7), в то время, как остальные имеют асимптотику O(N3).
tries = 10;
N = 10;
while N < 1000
taylortime = 0;
dbltime = 0;
expmtime = 0;
for it = 1:tries
A = rand(N);
A = 0.5 * (A + A');
tic;
B2 = argdbl(1, A, 1e-20, 1e10);
dbltime = dbltime + toc;
tic;
B3 = expm(A);
expmtime = expmtime + toc;
tic;
B1 = taylorexp(1, A, 1e-20, 1e10);
taylortime = taylortime + toc;
end
taylortime = 1e3 * taylortime / tries;
dbltime = 1e3 * dbltime / tries;
expmtime = 1e3 * expmtime / tries;
printf('%d,%f,%f,%fn', N, taylortime, dbltime, expmtime);
fflush(stdout);
N = round(N * 1.25);
end
Далее, проверим как алгоритм работает с большими по величине собственными значениями. Рассмотрим следующую систему обыкновенных дифференциальных уравнений:
С начальным условием:
.
Её особенность в том, что одно из ее собственных значений равно -1000 (быстро затухающее решение), а два других равны ±i√2 (колебательные решения). Если в мнимые собственные значения будут внесены искажения, это будет хорошо заметно. Возьмем шаг по времени τ = 0.038, найдем матричную экспоненту разными способами. Решение системы на сетке с шагом τ получается следующим простым алгоритмом:
- Решение в начальный момент известно из начального условия
- Зная решение un в момент tn, решение в момент tn+1 = tn + τ получается из него умножением на матричную экспоненту B:
- Повторять второй пункт, пока не будет достигнут конец отрезка интегрирования.
Посмотрим на полученные численные траектории (отображена только первая компонента вектора):
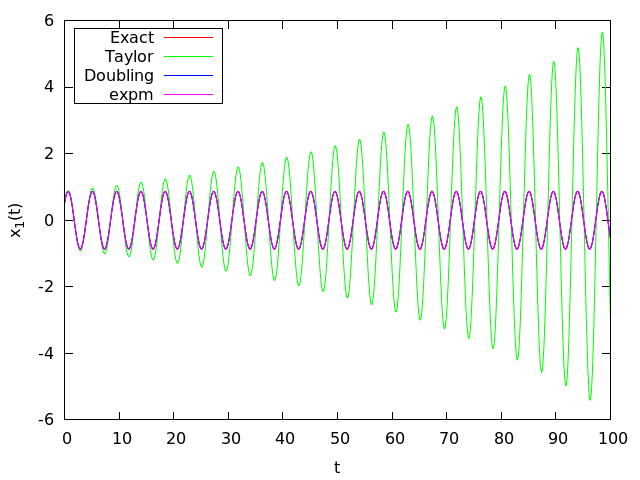
Все траектории, кроме полученной с помощью прямого суммирования ряда Тейлора, визуально совпадают. Обратите внимание, график не выходит из начального условия x1(0) = 1. На самом деле, график экспоненциально подходит к точке y = 1, просто характерное расстояние «поворота» графика (∼ 1 / 1000) намного меньше шага по времени τ = 0.038.
mu = 1000;
function [B] = trueexp(t, mu)
B = [
(exp(-mu*t) + cos(sqrt(2)*t))/2.,(-exp(-mu*t) + cos(sqrt(2)*t))/2.,sin(sqrt(2)*t)/sqrt(2);
(-exp(-mu*t) + cos(sqrt(2)*t))/2.,(exp(-mu*t) + cos(sqrt(2)*t))/2.,sin(sqrt(2)*t)/sqrt(2);
-(sin(sqrt(2)*t)/sqrt(2)),-(sin(sqrt(2)*t)/sqrt(2)),cos(sqrt(2)*t);
];
end
A = [-mu/2, mu/2, 1; mu/2, -mu/2, 1; -1, -1, 0];
t = 0:.038:100;
x0 = [1 0 1]';
B1 = trueexp(t(2), mu);
B2 = expm(t(2) * A);
B3 = taylorexp(t(2), A, 1e-20, 1e10);
B4 = argdbl(t(2), A, 1e-20, 1e10);
y1 = x0;
y2 = x0;
y3 = x0;
y4 = x0;
for i = 2:length(t)
y1 = B1 * y1;
y2 = B2 * y2;
y3 = B3 * y3;
y4 = B4 * y4;
printf('%f', t(i));
y = y1;
printf(' %e %e %e', y(1), y(2), y(3));
y = y2;
printf(' %e %e %e', y(1), y(2), y(3));
y = y3;
printf(' %e %e %e', y(1), y(2), y(3));
y = y4;
printf(' %e %e %e', y(1), y(2), y(3));
printf('n');
end
Можно сказать, что пример синтетический, и на практике не встретится, однако это не так. Существует множество так называемых жестких задач Коши, которые характеризуются сильным разбросом собственных значений (по сути, скоростей физических процессов).
Дальнейшее чтение
О различных способах вычисления матричной экспоненты можно почитать в статье (англ.) [2]. По методам решения обыкновенных дифференциальных уравнений и жестких задач написан замечательный двухтомник [3,4]
Список использованных источников
- Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во Моск. физ.-техн. ин-та, 1994. – 528с. § 17
- Cleve Moler and Charles Van Loan Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later // SIAM Rev., 45(1), 3–49. (47 pages)
- Хайрер Э., Нерсетт С., Ваннер Г.Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир,
1990. – 512 с. - Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. – 685 с.
Автор: Uranix
