ПИД-регулятор является простейшим регулятором, имеющим эффективные аппаратные аналоговые реализации, и потому применяемый наиболее широко. Для своей работы требует настройки 3х коэффициентов под конкретный объект, позволяющие подобрать процесс регулирования согласно требований. Обладая простым физическим смыслом и простой математической записью, применяется широко и часто в регуляторах температуры, регуляторах расхода газа и других системах, где требуется поддерживать некий параметр на заданном уровне, с возможными переходами между разными заданными уровнями. Разумеется, существуют более сложные регуляторы, позволяющие более точно и быстро и с меньшими перерегулированиями выходить на заданные параметры, а так же учитывающие нелинейность или гистерезис регулируемого объекта, однако они обладают большей вычислительной сложностью и сложнее в настройке.
Несмотря на свою простоту как физического смысла, так и математической записи:
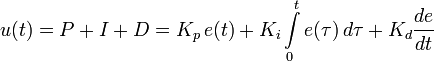
при програмной реализаци ПИД регулятора очень часто допускают ошибки, которые встречаются даже в поверенных приборах автоматики.
Причем проверить качество реализации ПИД регулятора крайне легко.
Рассмотрим простейший пример: терморегулятор. Для проверки его качестве лучше всего подходит быстрый, малоинерциальный, маломощный объект. Классика жанра: обычная лампочка на 100Вт с прикрученной к ней тонкой термопарой (ХА). И первое, на чем следует проверять ПИД регулятор — деградация ПИД до просто П-регулятора. То есть коэффициенты интегральной и дифференциальной ставим в ноль, а пропорциональную ставим в максимум.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит. Начинаем начинаем увеличивать уставку: 16.1, 16.3, 16.7, 18… 19… лампочка загорелась. Как?! Откуда?! Останавливаемся — выключилась. Итак, мы встретились с первой классической ошибкой реализации ПИД регулятора.
Небольшое математическое отступление: вспомним еще раз интегральную запись указанную выше. Мы реализуем её програмно, а значит — дискретно. То есть с завидной регулярностью производим измерение входной величины, сравниваем её с уставкой, вычисляем воздействие, выдаём, повторить. А значит, надо из интегральной формы перейти в конечно-разностную схему. При переходе обычно используется переход «в лоб»:
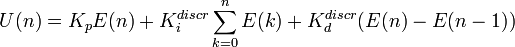
где E(n) = X(n) - X0(n) — то есть величина рассогласования между текущим и заданным значением регулируемого параметра.
Использование прямой формулы потребует во-1х считать и хранить интеграл рассогласований за большой период, во-2х требует работы с плавающей точкой высокой точности (так как интегральный коэффициент Ki всегда < 1), либо операции деления (представляя коэффициент в форме 1/Ki) большой разрядности. Всё это требует вычислительных ресурсов, коих в embedded как правило сильно ограничено… Поэтому, вместо реализации прямой схемы, реализуют рекуррентную формулу:
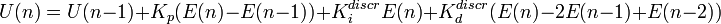
использование рекуррентной формулы позволяет сократить объём вычислений и разрядность промежуточных значений.
Итак, вернёмся к нашему регулятору. Итак, есть регулируемый объект: лампочка. Для управления подаваемой на неё мощностью, используют простой подход: сеть питания (220В 50Гц) подаётся через семистор на нагрузку. Семистор в момент перехода полуволны через ноль выключается, и остаётся выключен до тех пор, пока не будет подан сигнал на управляющий электрод. Таким образом, чем раньше после начала полуволны мы подадим управляющий сигнал, тем больше энергии от этой полуволны достигнет управляемого объекта. Правильно расчитав время для линейности площади части полуволны с момента времени X до конца полуволны, мы получаем возможность выдавать мощность от 0 до 100% с точностью, с которой расчитали таблицу линеаризации.
Итак, мы можем выдавать мощность от 0 до 100%. В реальных объектах, часто нельзя выдавать 100% мощности — например, это черевато перегоранием нагревательного элемента. Поэтому, все приборы имеют настройку минимальной и максимальной выдаваемой мощности на объект.
Итак, после вычисления U(n) по вышестоящей формуле, добавляется еще ограничение результата:
if Un < Umin then Un := Umin; if Un>Umax then Un := Umax;
После чего, вычисленное Un и есть требуемая выходная мощность на текущий момент. Та-дам! Именно вот эта реализация и создаёт ошибку, о которой написано выше.
Причина банальна: в момент перехода от дикретной к конечно-разностной схеме, мы «выносим за скобки» операцию вычисления интеграла, и на каждом шаге мы прибавляем производную к накопленной сумме U(n-1). Наложив же на неё ограничение, мы весь вычесленный интеграл фактически обнуляем. (Ну не сколько обнуляем, сколько приводим к диапазону 0-100, что в данном случае несущественно). Таким образом, мы дифференциурем ПИД регулятор, и остаётся дифференциально-ускорительный. Что в реальности выглядит как просто дифференциальный регулятор — мощность при этом подаётся пропорционально изменению уставки или регулируемой величины, а не пропорционально разности между уставкой и регулируемой величиной.
Вывод №1: вычисление U(n) нельзя ограничивать. Для ограничения мощности подаваемой на выходное устройство следует заводить отдельную переменную.
Теперь, когда мы завели Urn, для ограниченной мощности, перезаливаем, продолжаем тестировать.
Включаем регулятор, проверяем: текущая температура 22 градуса, уставка 16 градусов. Лампочка не горит.
Начинаем прибавлять уставку: 16.1, 16.4, 17, 18, 20, 22, 24 (опа! засветилось! ура!), 28, 30, 40, 60… Красота! Работает!
Наблюдаем за процессом — вышло примерно на 60, болтается чуток туда-сюда, но держит. Вроде, всё красиво. Выдыхаем, проверяем управление с ПК: задаём 600 градусов. И… Лампочка выключается. Как так? Уставка 600, текущая 60, а лампочка не горит?
Пока ждём и медленно осознаём, что мы явно напоролись на какой-то «Классический Косяк №2» ™ лампочка медленно разгорается, выходит на 100% мощности, и так и остаётся — 600-то градусов она выдать ну никак не может.
Возвращаемся снова к нашей разностной схеме. U(n) = U(n-1) + Kp*(dE + ...). К текущему расчетному значению воздействия прибавляется разность невязки помноженная на коэффициент пропорциональности. У нас была уставка 60, температура 60, то есть невязка нулевая. Выходная мощность так же была нулевая. И тут разом, скачком, уставку увеличили до 600 градусов. невязка резко стала 540 градусов, помножили еще и на коэффициент пропорциональности… и вылетели за разрядность хранения U(n). Не смейтесь, использование математики с фиксированной точки, вместо плавающей точки. При разнице в 540 градусов и работе через 1/16, при коэффициенте пропорциональности 20, получаем… 540*20*16=172800, а если у нас 16тиразрядный U(n), да еще и знаковый, то фактически, в результате вычисления мы получили A300h = −8960. Опачки. Вместо большого плюса — ощутимый такой минус.
Вывод №2: вычисления должны проводиться с корректной поддержкой переполнения. Переполнилось? Ограничь предельным числом, уж никак не заворачивать.
Итак, нарастили разрядность U(n), перетранслировали, зашили, запускаем. Лампочка еще не совсем остыла, там 80 градусов, уставка всё те же 600. Лампочка зажигается… и тухнет. Зажигается и тухнет. Как так? Уставка 600, лампочка 80 — и поддерживает вполне себе свои 80! Как так-то?! Явно у нас вылез Жучок №3.
И снова лирически-математическое отступление. Итак, есть наша разностная схема: U(n) = G(U(n-1), dE(n)). Еще раз: новое значение воздействия есть сумма прошлого воздействия и некого воздействия, зависящего от разности невязки в текущий момент и предыдущий. А что такое предыдущий момент? А какой момент предыдущий у предыдущего? Ну-ка, вспомнили школу. Доказательство по индукции. Если можно построить доказательство для K+1, считая что доказательство для K верно, И доказать отдельно что верно для K=0, тогда доказательство истинно. Итак, а как мы считаем U(0)?
Часто встречающееся решение: всё обнуляем, уставку считываем из флешпамяи уставки, ждём 1 цикл опроса, и считываем X(0). Вот, ноль готов, теперь работаем. И… И не правильно. Почему? Потому что рекурентная формула отталкивается от изменений в невязке. А проинициализировав нулём и загрузив текущие значения мы потеряли стартовые условия. Всё — вместо поддержания абсолютного значения температуры на уровне равном абсолютной уставке регулятор начинает держать температуру равную стартовой плюс разнице уставки. То есть было 80 градусов и уставка 200, включили прибор — он держет 80. Сменили уставку на 240 — он начал держать 120.
Правильная инициализация разностной схемы: обнулить _вообще всё_. То есть
X(0) = 0, X0(0) = 0. U(0) = 0. E(0)=X(0)-X0(0)=0.
И на первом же цикле вычислений у нас как бы скачком появляются уставке и текущее значение:
X(1) = 80. X0(1)=200. U(1) = U(0)+Kp*(E(1)-E(0)) = U(0)+Kp*(X(1)-X0(1)-E(0)) = 0 + 20*(200 - 80 - 0) = 2400
Вот теперь схема работает правильно.
Вывод №3: корректно инициализируй стартовые условия.
Правильно ли? Hу-ка, ну-ка... Еще раз... Ставим уставку 20. Ждём охлаждения... Выключаем. Включаем. Итак, красота: текущая 20, уставка 20. Ставим скачком 600. Поехало греться. 100, 120... ставим уставку 20. Отключилось, пошло охлаждаться. Ждём чуток (120... 110... 100... 90... 80...) и ставим уставку 100. Поехало греться... 105 градусов, отключилось. Стоп. А почему оно держит 105? У нас же сейчас работает только пропорциональная составляющая. При правильной реализации из физического смысла процесса колебательный процесс не может держать уставку выше чем задано. Строго ниже. А держит на 5 градусов больше чем попросили. Это наблюдается Прикол №4.
Итак, вспоминаем что у нас было выше: Вывод№2: U(n) нельзя ограничивать. И Вывод№3: при переполнении ограничить всё-таки придётся. Да-да. Иначе "рабочая точка" смещается на ограниченный момент. Что же делать? Увеличить разрядость? Хорошо, если хватает вычислительной мощности. А надо ли? Собственно, что плохого, что у нас U(n) = 9999.99, а не 29999.99 ? В общем-то только то, что мы потеряли 20000. Но сейчас-то для работы нам так и так надо вваливать просто 100% мощности, правильно? Правильно. Значит, проблемы с ограничением в полку нет, до тех пор, пока мы не отходим от предела. Таким образом, в случае переполнения надо ставить флаг, и по достижении, например, половины диапазона (то есть как U(n) после 9999.9 опустилось ниже 5000.00), заново реинициализировать схему. То есть отбрасывать историю, сказать что n=0 и см. выше Вывод №3. Пытливый ум уже сообразил, что в случае полной схемы, когда все три компоненты не равны нулю, обнуляя в процессе итеративный процесс, мы в том числе обнуляем накопленный интеграл интегральной составляющей. Однако, в связи с тем, что обнуляем мы значительно заранее, он успеет подкопиться за время довырабатывания остатка. Да и не совсем корректно копить интеграл на "больших" перегонах, так как цель интегральной составляющей -- "выбрать" невязку, которую не может отработать пропорциональная составляющая отдельно.
Вывод №4: если по какой-то причине U(n) было ограничено, схему следует переинициализировать как только создалось впечатление, что схема вернулась в нормальное состояние.
В следующем выпуске: а так ли надо реализовывать разностную схему? Подробная реализация прямой дискретной схемы, обладающей простыми и понятными настраиваемыми коэффициентами, с прямым физическим смыслом, которая без проблем вычисляет управляющее воздействие с частотой 25Гц на процессоре ADuC847 (быстрый 8-битный контроллер, с ядром 8051), оставляя еще море процессорного времени для других процессов.
(Картинки с изображением формул взяты из статьи ПИД-Регулятор в Wikipedia)
Автор: datacompboy




