Все из нас когда-либо играли в карты. И любой держал в руках, мешал карточную колоду. Вот и я, как-то сидя и перемешивая стандартную колоду из 52 карт, задумался, а какова вероятность того, что результат будет уникальным? Что никто и никогда после перемешивания не получал карты в колоде в том порядке, что и я?
Казалось бы, первое, что приходит в голову — вероятность мала. Ведь люди постоянно играют в карты. А если учесть то, что люди непрерывно играют в покер в интернете, так вообще, наверное, все варианты давно перепробованы… Или нет?
Оценка сверху.
Для начала скажу, что под перемешиванием я буду подразумевать порядок карт, полученный после случайной тасовки колоды.
Попробуем оценить сверху количество перемешиваний колоды, сделанных всеми людьми за всю историю. При этом предположим, что каждый раз получалась уникальная колода (ну а вдруг?). Посчитаем с большим запасом.
Для начала разберемся с электронными играми (будем считать, что колода там тоже мешается, а не генерируется по ходу игры). Пусть есть 1000000 (миллион) различных игровых серверов. Много, наверное? Ну так мы же с запасом считаем. И пусть в них каждую секунду тасуется десяток колод. Тогда в день тасуется: 10*60*60*24*1000000=864*10^9 колод. А в живую? В любом случае, по сравнению с электронными играми, число будет сильно меньше. Поэтому (чтобы не сильно заморачиваться, ведь мы берем грубую оценку сверху) просто удвоим получившееся число. И округлим в большую сторону: 1728*10^9 < 2*10^12 перемешиваний. Итак, мы оценили сверху количество перемешиваний в день в наше время.
А за всю историю?
Разумеется, мы знаем, что компьютеры появились не столь давно, что раньше карты уж точно мешали вручную. Но мы ведь берем оценку сверху? Грубую оценку сверху. Так что будем считать, что всегда в день мешалось минимум столько колод, сколько и сейчас. Как подсказывает Википедия, история современного вида карточной колоды уж точно насчитывает меньше тысячи лет. Будем исходить из этого. За тысячу лет прошло: 365000 дней. Тогда за всю историю было произведено уж точно меньше, чем 365000*2*10^12 = 73*10^16 перемешиваний. Для удобства будем использовать несколько большее число 10^18.
Вспомним, что оценка бралась очень и очень завышенная. Поэтому точно за всю историю не совершалось больше, чем 10^18 перемешиваний колоды (если только какой-то суперкомпьютер не мешал колоду целыми сутками, но об этом в конце статьи).
Расчет вероятности.
Так какова теперь вероятность получить при перемешивании новый вариант расположения карт?
Для начала, посмотрим, чему равно количество вариантов расположения карт вообще. Это 52! = 52*51*50*...*2*1. По формуле Стирлинга это приблизительно равно:
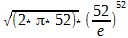= 8*10^67.
Таким образом, вероятность, что свежеперемешанную колоду уже когда-то кто-то получал заведомо меньше, чем 10^18/(8*10^67) = 1.2*10^(-50). Да-да, вероятность, что колода НЕ уникальна — чрезвычайно мала. Таким образом можно дать ответ на вопрос, поставленный вначале топика:
Вероятность получить при перемешивании уникальную колоду заведомо больше, чем 99.999...999% (после десятичной точки следуют 50 девяток). Неожиданно? Да, довольно неожиданно даже для человека, знакомого с теорией вероятностей.
Причем, если учесть, что расчет был очень грубый, то реальная вероятность еще больше.
Бонус.
А теперь посчитаем, сколько времени нужно, чтобы перебрать все эти варианты на компьютере. Самые современные суперкомпьютеры, если верить Википедии, выполняют порядка 10^16 операций в секунду. В день — 60*60*24*10^16 = 864*10^18. В год — примерно 3*10^23. Так сколько лет нужно, чтобы перебрать все 8*10^67 вариантов перемешиваний колоды? Что-то вроде миллиарда миллиардов миллиардов миллиардов миллиардов лет. Вдуматься, даже страшно становится. Причем даже если направить в помощь этому суперкомпьютеру все остальные вычислительные средства планеты, это не сильно поможет. Все равно потребуются миллиарды и миллиарды лет. А ведь это всего лишь колода из 52 карт. Что уж говорить о количестве партий игры в Го? :)
Автор: Lonsdaleite
