О формуле Байеса, прогнозах и доверительных интервалах

На Хабре много статей по этой теме, но они не рассматривают практических задач. Я попытаюсь исправить это досадное недоразумение. Формула Байеса применяется для фильтрации спама, в рекомендательных сервисах и в рейтингах. Без нее значительное число алгоритмов нечеткого поиска было бы невозможно. Кроме того, это формула явилась причиной холивара среди математиков.

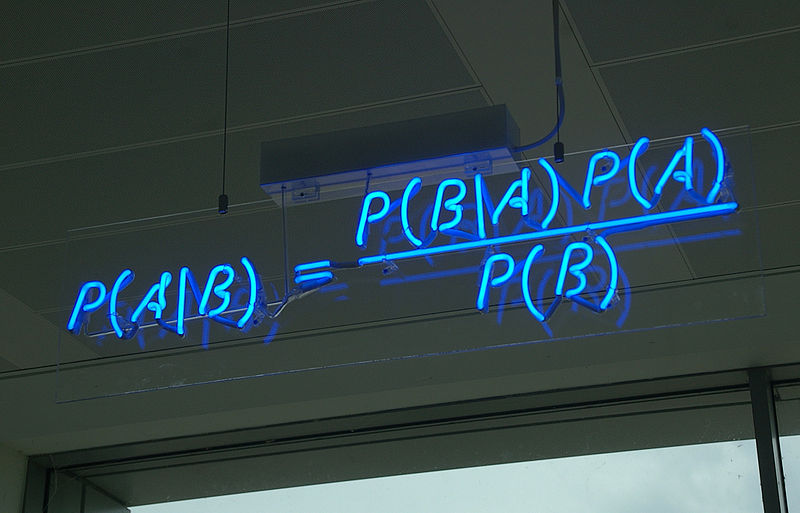
Введение

Начнем издалека. Если наступление одного события увеличивает или уменьшает вероятность наступления другого, то такие события называются зависимыми. Тервер не изучает причинно-следственные связи. Поэтому зависимые события не обязательно следствия друг-друга, связь может быть не очевидной. Например, «у человека голубые глаза» и «человек знает арабский» — зависимые события, поскольку у арабов голубые глаза встречаются крайне редко.

Теперь следует ввести обозначения.

• P(A) значит вероятность наступления события A.
• P(AB) вероятность наступления обоих событий вместе. Не важно в каком порядке наступают события P(AB)=P(BA).
• P(A|B) вероятность наступления события А, если событие B произошло.

Давайте подумаем чему равно вероятность наступления двух событий одновременно. P(AB). Вероятности наступления первого события умноженной на вероятность наступления второго события, в случае наступления первого. P(AB)=P(A)P(B|A). Теперь, если вспомнить, что P(AB)= P(BA). Получим, P(A)P(B|A)=P(B)P(A|B). Перенесем P(B) влево и получим формулу Байеса:

Все настолько просто, что 300 лет тому назад эту формулу вывел простой священник. Но это не уменьшает практической ценности этой теоремы. Она позволяет решать «обратную задачу»: по данным испытаний оценить ситуацию.

Прямая и обратная задачи

Прямую задачу можно описать так: по причине найти вероятность одного из следствий. Например, дана абсолютно симметричная монета (вероятность выпадения орла, как и решки, равны 1/2). Нужно посчитать вероятность того, что если мы дважды подкинем монету, оба раза выпадет орел. Очевидно, что она равна 1/2 * 1/2 =1/4.

Но проблема в том, что мы знаем вероятность того или иного события только в меньшинстве случаев, почти все их которых искусственные, например, азартные игры. При этом в природе нет ничего абсолютного, вероятность выпадения орла у реальной монеты равна 1/2 только приблизительно. Можно сказать, что прямая задача изучает некоторых сферических коней в вакууме.

На практике, важнее обратная задача: оценить ситуацию по данным испытаний. Но проблема обратной задачи в том, что ее решение сложнее. Главным образом из-за того, что наше решения будет не точкой P=С, а некоторой функцией P=f(x).

Например, у нас есть монета, нужно оценить с помощью опытов вероятность выпадения решки. Если мы подкинули монету 1 раз и выпал орел, то это не значит, что всегда выпадают орлы. Если 2 раза подкинули и получили 2 орла, то опять это не значит, что выпадают орлы. Чтобы получить абсолютно точно вероятность выпадения решки, мы должны подкинуть монету бесконечное число раз. На практике это не возможно и мы всегда вычисляем вероятность события с некоторой точностью.

Мы вынуждены использовать некоторую функцию. Обычно ее принято обозначать как P(p=x|s решек, f орлов) и называть плотностью вероятности. Читается это так вероятность, того, что вероятность выпадения орла равна x, если по данным эксперимента выпало s решек и f орлов. Звучит сложно звучит из-за тафтологии. Проще считать p некоторым свойством монетки, а не вероятностью.

Забегая вперед скажу, что если в первую монетку подкинем 1000 раз и получим 500 орлов, а вторую 10000 и получим 5000 орлов, то плотности вероятности будут выглядеть так:

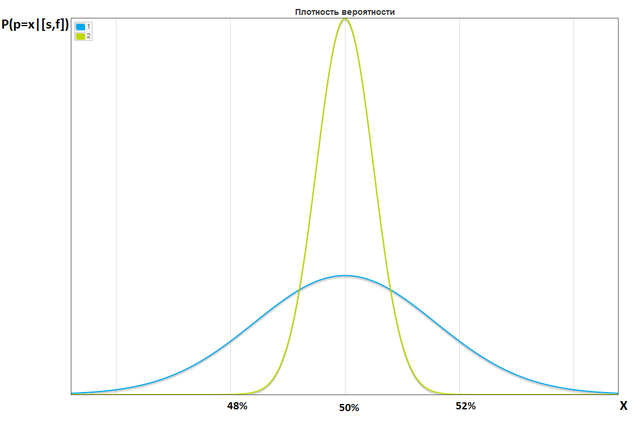
Из-за того, что у нас не точка, а кривая мы вынуждены использовать доверительные интервалы. Например, если говорят 80% доверительный интервал для p равен 45% до 55%, то это значит с 80% вероятностью p находиться между 45% и 55%.

Биномиальное распределение

Для простоты будем рассматривать биномиальное распределение. Это распределение количества «успехов» в последовательности из некоторого числа независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна. Оно наблюдается практически всегда, когда у нас есть последовательность испытаний с двумя возможными исходами. Например, когда мы несколько раз подкидываем монету, или оцениваем CTR банера, или конверсию на сайте.

Для примера будем считать, что нам нужно оценить вероятность выпадения решки у монеты. Мы подкинули монету некоторое число раз и получили f орлов и s решек. Обозначим это событие как [s,f] и подставим это в формулу Байеса вместо B. Событие когда p равно некоторому числу будем обозначать как p=x и подставим вместо события А.

P([s,d]|p=x), Вероятность получить [s,d], если p=x, при условии, что p=x нам известна P([s,f]|p=x)=K(f,s) * x^s (1-x)^f. Где K(f,s) биномиальный коэффициент. Получаем:

Нам неизвестна P([s,f]). Да и биномиальный коэффициент вычислить проблематично: там факториалы. Но эти проблемы можно решить: суммарная вероятность всех возможных p должна быть равна 1.

С помощью простых преобразований мы получим формулу:

Программируется это просто, всего 10 строк:

    //f(x) некторая функция  P(p=x)
    m=10000;//число точек
    eq=new Array(); //P(p=x|[s,f])
    sum=0;
    for(i=0;i<m;i++){
         x=i/m;// от 0 до 1
         eq[i]= f(x) * x^cur.s*(1-x)^cur.f; // С * P(p=x|[s,f]) с точностью до постоянного коефициента
         sum+=eq[i]
    }
    //Сумма должна быть 1
    for(i=0;i<m;i++)
       eq[i]/=sum;

Однако, у нас остается неизвестной P(p=x). Она выражает, насколько вероятно, что p=x, если данных по эксперименту у нас нет. Эту функцию принято называть априори. Из-за нее и произошел холивар в теории вероятностей. Вычислить априори строго математически мы не можем, только задать субъективно. А без априори мы не можем решить обратную задачу.

Холивар

Сторонники классической интерпретации (частотного подхода, ЧП), считают, что все возможные p равновероятны до начала эксперимента. Т.е. перед экспериментом нужно «забыть» те данные, которые нам известны до него. Их оппоненты, сторонники байесовского подхода (БП), считают, что нужно задать какую-то априори исходя из наших знаний до начала эксперимента. Это фундаментальное отличия, даже определение понятия вероятности у этих групп разное.

Кстати, создатель этой формулы, Томас Баейс умер лет на 200 раньше холивара и отношение к этому спору имеет только косвенное. Формула Байеса часть обоих конкурирующих теорий.

Частотный подход(ЧП) лучше подходит для науки, где нужно объективно доказать какую-то гипотезу. Например, то что смертность от препарата меньше определенного порога. Если же вам нужно, учитывая всю доступную информацию, принять решение, то лучше использовать БП.

ЧП не подходит для прогнозирования. Кстати, формулы доверительных интервалов, считают доверительные интервал по ЧП. Сторонники БП, обычно, в качестве априори для биномиального распределения используют Бета распределение, при a=1 и b=1 оно вырождается в непрерывное распределение, которое используют их противники. В итоге формула принимает вид:

Это универсальная формула. При использовании ЧП нужно задать b=a=1. Сторонники БП некоторым образом должны выбрать эти параметры, так чтобы получилось правдоподобное бета-распределение. Зная a и b можно использовать формулы ЧП, например для расчета доверительного интервала. Например, мы выбрали a=4.5, b=20, у нас есть 50 успехов и 100 неудач, чтобы вычислить доверительный интервал в БП нам нужно в обычную формулу ввести 53.5 (50+4.5-1) успеха и 119 неудачу.

Однако, у нас нет никаких критериев выбора a и b. Следующая глава расскажет как их выбрать по статическим данным.

Прогноз

Логичнее всего в качестве прогноза использовать мат. ожидание. Его формулу легко получить из формулы мат. ожидания бета-рапределения. Получим:

.

Например, у нас есть сайт, со статьями. На каждой из них есть кнопка «лайк». Если мы будем сортировать по числу лайков, то у новых статей мало шансов перебить старых. Если мы будем сортировать по соотношению лайков к посещениям, то статьи с одном заходом и одним лайком будут перебивать статью с 1000 заходами и с 999 лайками. Разумнее всего сортировать по последней формуле, но нужно каким-то образом определить a и b. Самый простой способ через 2 основных момента бета-распределения: мат. ожидание (сколько в среднем будет) и дисперсию (каково в среднем отклонение от среднего).

Пусть L средняя вероятность лайка. Из матожидания бета-распределения L=a/(a+b) =>a+b=a/L=> aL+bL=a => b=a(1/L — 1). Подставим в формулу дисперсии:

На псевдокоде это будет выглядеть так:

L=0;
L2=0;//Сумма квадратов
foreach(articles as article){
    p=article.likes/article.shows;
    L+=p;
    L2+=p^2;
}
n=count(articles);
D=(L2-L^2/n)/(n-1);//Дисперсия
L=L/n;//среднее
a=L^2*(1-L)/D-L;
b=a*(1/L — 1);

foreach(articles as article)
   article.forecast=(article.likes+a-1)/(article.shows+a+b-2)

Не смотря на то, что данный выбор a и b кажется объективным. Это не строгая математика. Прежде всего не факт, что лайкабельность статей подвержена Бета-распределению, в отличии от биномиального это распределение «не физично», оно введено для удобства. Мы по сути подогнали кривую к статистическим данным. Причем вариантов подгонки есть несколько.

Шанс побить всех

Например, мы провели А/B тест нескольких вариантов дизайна сайта. Получили некоторые результаты и думаем, нужно ли его останавливать. Если мы остановимся слишком рано мы можем выбрать не верный вариант, но остановиться когда-то все-таки нужно. Мы можем оценивать доверительные интервалы, но их анализ сложен. Как минимум, поскольку в зависимости от коэффициента значимости у нас получаются разные доверительные интервалы. Сейчас я покажу как посчитать вероятность того, что один вариант лучше всех остальных.

Кроме зависимых событий существуют и независимые события. Для таких событий P(A|B)=P(A). Поэтому P(AB)=P(B)P(A|B)=P(A)P(B). Для начала нужно показать что варианты независимы. Кстати сравнивать доверительные интервалы корректно, только в случае когда варианты независимы. Как уже было сказано, сторонники ЧП отбрасывают все данные кроме самого эксперимента. Варианты это отдельные эксперименты, поэтому каждый из них зависит только от своих результатов. Поэтому они независимы.

Для БП доказательство сложнее, основной момент, что априори «изолирует» варианты друг от друга. Например, события «голубые глаза» и «знает арабский» зависимы, а события «араб знает арабский» и «у араба голубые глаза» нет, поскольку взаимосвязь между первыми двумя событиями исчерпывается событием «человек араб». Более верная запись P(p=x) в нашем случае следующая: P(p=x|apriori=f(x)). Поскольку все зависит от выбора функции априори. А события P(p_i=x|apriori=f(x)) и P(p_j=x|apriori=f(x)) независимы, поскольку единственная взаимосвязь между ними это функция априори.

Введем определение P(p<x), вероятность того, что p меньше x. Очевидна формула:

Мы просто «сложили» все точечные вероятности.

Теперь отвлечемся, и я вам объясню вам формулу полной вероятности. Допустим есть 3 события A,B,W. Первые два события взаимоисключающие и при этом одно из них должно произойти. Т.е. из этих двух событий всегда происходит не более и не менее одного. Т.е. должно произойти либо одно событие либо другое, но не вместе. Это например, пол человека или выпадение орла/решки в одном броске. Так вот Событие W может произойти только в 2 случаях: совместно с А и совместно с B. P(W)=P(AW)+P(BW)=P(A)*P(W|A)+P(B)*P(W|B). Аналогично происходит когда событий больше. Даже когда их бесконечное число. Поэтому мы можем совершать такие преобразования:

Допустим у нас есть n вариантов. Мы по каждому из знаем число успехов и неудач. [s_1,f_1], ..., [s_n,f_n]. Для упрощения записи будем упускать данные из записи. Т.е. вместо P(W|[s_1,f_1], ..., [s_n,f_n]) просто будем писать: P(W). Обозначим вероятность того, что вариант i лучше всех остальных (Chance To Beat All) и проведем некоторое сокращение записи:

∀j≠i значит для любых j не равных i. Говоря простыми словами это все значит вероятность того, что p_i больше всех остальных.

Применим, формулу полной вероятности:

Первое преобразование просто изменяет форму записи. Второе подставляет x вместо p_i, поскольку у нас есть условная вероятность. Поскольку p_i не зависит p_j, то можно выполнить третье преобразование. В итоге получили, что это равно вероятности того, что все p_j кроме i меньше x. Поскольку варианты независимые, то выполняется P(AB)=P(A)*P(B). Т.е. это все преобразуется в произведение вероятностей.

В итоге формула примет вид:

Это все можно вычислить за линейное время:

	m=10000;//число точек
	foreach(variants as cur){    
		cur.eq=Array();//P(p=x)
		cur.less=Array();//P(p<x)
		for(i=0;i<m;i++){
			x=i/m;
			cur.eq[i]= x^cur.s*(1-x)^cur.f;//С*P(p=x) с точностью до постоянного коефициента
			cur.less[i]+=cur.eq[i];
		}
		//cur.less[m-1]  и сумма всех cur.eq  должны быть равны 1
		for(i=0;i<m;i++){
			cur.eq[i]/=cur.less[m-1];
			cur.less[i]/=cur.less[m-1];  
		}
	}
	
	//Произведение P_j(p<x)
	lessComp=Array();
	for(i=0;i<m;i++){
		lessComp[i]=1;// заполнить массив единицами
		foreach(variants as cur)
			lessComp[i]*=cur.less[i]
	}
	foreach(variants as cur){ 
		cur.ctba=0;//Chance To beat All
		for(i=0;i<m;i++)
			cur.ctba+=cur.eq[i] * lessComp[i] /cur.less[i];
	}

Для простого случая когда есть только два варианта (Chance to beat baseline/origin, CTBO). используя нормальную аппроксимацию можно вычислить этот шанс за константное время. В общем случае решить за константное время нельзя. По крайней мере, Google это не удалось в Google WebSite Optimizer были и CTBA и CTBO, после переноса в Analytics остался менее удобный CTBO. Единственное объяснение этому в том, что ресурсов на вычисление CTBA тратиться слишком много.

Кстати понять правильно ли вы организовали алгоритм можно по двум вещам. Суммарный CTBA должен быть равен 1. Также можно сравнить ваш результат со скриншотами Google WebSite Optimizer. Вот сравнения результатов нашего бесплатного статистического калькулятора HTraffic Calc с Google WebSite Optimizer.

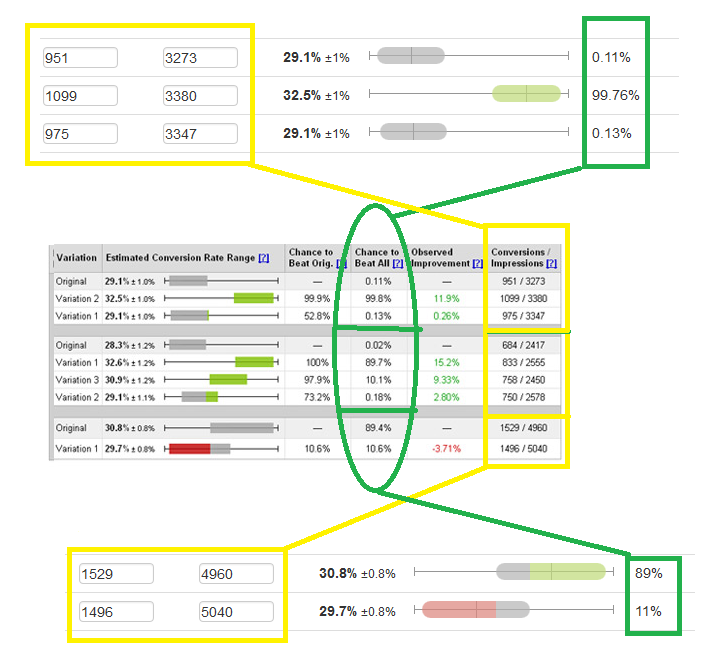
Разница в последнем сравнении обусловлена в том, что я использую «умное округление». Без округления данные одинаковые.

В общем вы можете HTraffic Calc для тестирования своего кода, поскольку в отличии от Google WebSite Optimizer он позволяет вводить свои данные. Также можно с его помощью сравнивать варианты, однако, следует учитывать фундаментальные особенности CTBA.

Особенности CTBA

Если вероятность успеха далеко от 0.5. При этом число испытаний (например, бросков монеты или показов баннера) в некорых вариантах мало и при этом число вариантов отличается в разы, то вы должны либо задавать Априори либо выровнять число испытаний. Тоже самое касается не только CTBA, но и сравнения доверительных интервалов.

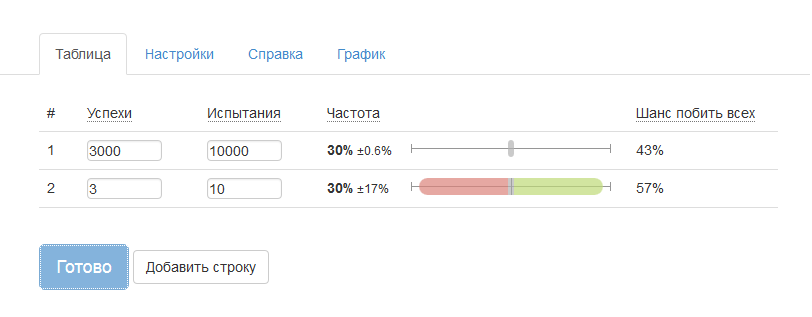
Как мы видим из скриншота у второго варианта выше шансы побить первый. Это происходит из-за того, что мы выбрали в качестве априори равномерное распределение, а у него мат ожидание равно 0.5, это больше 0.3 поэтому в этом случае вариант с меньшим числом испытаний получил некоторый бонус. С точки зрения ЧП эксперимент нарушен — у всех вариантов должно быть равное число испытаний. Вы должны выровнять число испытаний, отбросив часть испытаний у одного из вариантов. Или использовать БП и выбрать априори.

Автор: Hkey

Источник