Одной из актуальных проблем информационной безопасности является конфиденциальность сообщений, которая обеспечивается в RSA-подобных шифрах применением криптографической защиты сообщений. Подобная защита успешно реализуется при знании закона распределения делителей составного числа (модуля кольца вычетов) в натуральном ряде чисел (НРЧ) и наличии криптографической системы (КГС), в рамках которой и циркулируют сообщения.
Основу КГС составляют алгоритмы шифрования, система управления ключами шифрования, криптографические протоколы, функции хеширования и электронная подпись. Каждый шифр и соответственно алгоритм шифрования имеет набор характеристик, на основании которого пользователи осуществляют выбор для применения того или иного шифра. Очевидно, что предпочтение отдается шифру с достаточно высоким уровнем стойкости к вскрытию ключа шифра и соответственно содержания защищаемого сообщения.
Время жизни качественных шифров до момента их раскрытия и публикации об этом исчисляется годами, а очень качественных десятилетиями. Среди симметричных и асимметричных шифров весьма популярным является двухключевой шифр RSA. Он известен с 1978 года, года первой публикации с описанием алгоритма.
Стойкость этого шифра определяется невозможностью решения математической задачи факторизации большого числа (ЗФБЧ) — модуля шифра за приемлемое для пользователя время. Это время исчисляется годами. Например, составное число из 232 десятичных цифр было факторизовано в 2010 году, а объявлено оно в списке на сайте RSA среди прочих в 1991 году. Список начинается числом из 100 цифр. Первые 18 чисел за прошедшие годы усилиями математиков всего мира и ПК последовательно раскладывались все прошедшие годы, что свидетельствует о большом интересе математиков к этой проблеме. Последнее число списка содержит 617 цифр, что соответствует ключу шифра длиной 2048 двоичных разрядов.
Основные положения теории
В предлагаемой вниманию работе затрагивается проблема факторизации натуральных чисел. Осуществляется привязка заданных N и определяемых объектов (делителей) к основному объекту — НРЧ. Использование свойств НРЧ и свойств составных чисел, не связанных с их разрядностью, указывают другое направление для поиска решения проблемы факторизации. Приведенная теорема и пример 3 указывают, на какие элементы необходимо обратить основное внимание, локализуют эти элементы в пределах НРЧ, ограничивают области поиска. Сами области получают модельное описание.
В работе задача формулируется следующим образом. Составное число N задано положением на оси натурального ряда чисел, где каждому числу определена индексированная позиция. Требуется определить натуральные делители — факторы N. Факторы (делители) числа также размещены в своих позициях НРЧ, которые всегда расположены ближе к началу, левее позиции N. Все позиции от нуля до N — 1 заняты меньшими N числами, образующими конечное кольцо вычетов по составному модулю, роль которого играет N. Очевидно, что среди меньших чисел (элементов кольца вычетов) встретятся и делители, а если делители малы, то и кратные этих делителей. Всегда можно указать два составных делителя, если для N их больше двух, или два простых. Пусть собственных делителей будет только два, т.е. N = pq.
Cформулируем теорему о делителях составного N.
Теорема. Квадрат полуразности делителей сравним по модулю их произведения N с квадратом полусуммы делителей, что формально запишется так [(p-q)/2]2≡[(p+q)/2]2(modN).
Действительно, для правой части, учитывая, что N = pq, возводя в квадрат полусумму и раскрывая скобки, получаем выражение
(р2 +2pq +q2 — 4N)/4 = (р2 — 2pq +q2)/4 = [(p-q)/2]2,
совпадающее с левой частью, что и доказывает теорему.
Из теоремы следует, что среди элементов кольца вычетов по составному модулю N имеется такой элемент х, квадрат которого по модулю N совпадает с квадратом полусуммы делителей и разность этого квадрата с модулем кольца равна другому элементу r кольца, значение которого совпадает с квадратом полуразности делителей. Нахождение таких элементов кольца позволяет сформировать замкнутую систему алгебраических уравнений, решением которой будут искомые делители.
Пример 1. Пусть задана пара натуральных простых чисел p = 47, q = 67 и N = pq = 3149. Вычислим для делителей полусумму (67+47)/2 = 57, и (67- 47)/2 =10 их полуразность, а также выполним преобразования правой части 572 — 3149 = 3249 — 3149 = 100 =102, что совпадает с квадратом левой части выражения из теоремы.
Полусумма делителей — первый (меньший) элемент кольца (точка х НРЧ), который приводит к разложению N на множители. Конечно, такая точка нам неизвестна, так же как и точка полуразности делителей.
В алгебраических конечных кольцах вычетов по составному модулю при лексикографическом упорядочении элементов по возрастанию все квадратичные вычеты (КВВ) также упорядочены, но на первый взгляд их последовательность выглядит достаточно хаотичной.
Такую последовательность КВВ удобно разбить на три части. Первую, начальную часть назовем тривиальной. Она образована квадратичными вычетами по модулю N — полными квадратами, так как элементы квадрат, которых меньше модуля не редуцируются (не приводятся по модулю). В эту часть включим по порядку следования и все квадратичные вычеты — не являющиеся полными квадратами. Далее следует средняя часть, левой границей которой является первый встретившийся квадратичный вычет — полный квадрат. Таким образом, все, что до него — начальная часть. Конечная часть списка КВВ отделена от средней части позицией НРЧ, в которой появляется последний квадратичный вычет — полный квадрат. Последней части может не быть вообще, если квадратичный вычет элемента (N-1)/2 оказывается полным квадратом. Это достаточно распространенная ситуация, она имеет место для канонического составного модуля.
Пример 2. Пусть задан модуль шифра N = d1•d2 = 2091. Делители в общем случае неизвестны.
В этом примере точкой, которой начинается средняя часть последовательности квадратичных вычетов, является позиция, следующая сразу за тривиальной частью. Тривиальная часть списка включает квадраты от 1 до 45, (до ближайшего снизу квадрата к модулю, не превышая его), и уже следующая позиция, равная х = 46 (46 < N, 462 >N) имеет квадратичным вычетом полный квадрат, 462(modN) = 25. При этом делители N находятся из соотношения di = 46 ± √25 = 46 ± 5, откуда d1 =46+5 = 51 и d2 = 46 — 5 = 41. Для этого случая легко убедиться, что сказанное ранее о свойствах делителей верно.
Вычислим полусумму (51+41)/2 = 46, полуразность (51 — 41)/2 = 5 и выполним преобразования правой части 462 — 2091 = 52= 25, что совпадает с квадратом левой части соотношения из теоремы. Полусумма делителей действительно первая точка, которая приводит к разложению N на множители.
Замечательным фактом является также то, что быстрый поиск делителей определяется не только такой первой точкой (до нее не так -то просто бывает добраться), а любым квадратичным вычетом — полным квадратом. Следующий пример иллюстрирует возможности квадратичных вычетов конечного кольца, если они являются полными квадратами.
Иллюстрация закона распределения делителей составного модуля
Пример 3. Задан составной модуль N =119. Необходимо найти точки НРЧ, в которых х<N, x2 >N и x2(mod N) = r(x) = ⃞ — полный квадрат, где х — текущая точка НРЧ. После выполнения всех необходимых преобразований можно получить результаты, сведенные в таблицу 1.
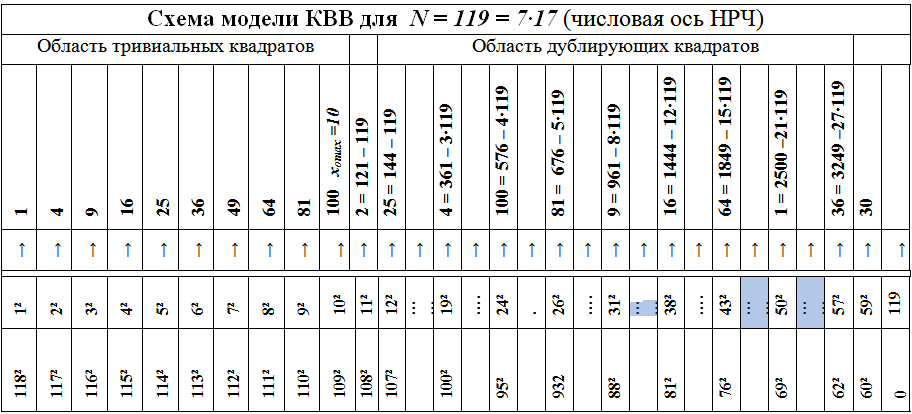
Краткий комментарий к таблице.
Две нижние строки таблицы содержат: предпоследняя — квадраты текущих элементов х кольца, а последняя строка — квадраты их дополнений х1, где х1 = N — х. Четвертая снизу строка содержит КВВ элементов кольца, которые являются полными квадратами (исключение точки х = 11, ее КВВ r(11) = 2 и х = 59, ее КВВ r(59) = 30 ). Такая картина распределения квадратичных вычетов конечного кольца вычетов имеет место всегда. Это послужило основанием для формулирования Закона распределения делителей (ЗРД) составного натурального числа. Закон формулируется так.
Законом распределения делителей di, i = 1(1)..., составного числа N называется соотношение, определяющее множество позиций НРЧ, в которых размещаются делители и кратные им значения, зависящие от заданного N. Все делители и кратные им — это значения в граничных точках интервалов, симметричных относительно точек х < N, x2 >N, x2(mod N) = r(x), в которых КВВ r(x) являются полными квадратами, т.е. di = х±√r(x), i = 1(1)… .
После получения х с указанным свойством находят пары значений d1, d2. Число N можно поделить на них и найти таким же способом другие делители для частного меньшего N. Если полученные d1, d2 не простые числа, то применяя Алгоритм НОД Евклида к любому из d1, d2 и модулю N, находят их очередной общий делитель. Так действуют до полного разложения N на простые множители.
В работе не описывается путь нахождения х, исключающий полный перебор, и автор понимает какие проблемы встретятся на этом пути. Отдельные подготовительные вопросы к решению этой проблемы автором представлены в его предшествующих публикациях.
Автор: VAE





очень интересная статья. большое спасибо автору