Прочитав статью «Динамическая система Лоренца и вычислительный эксперимент», проверил расчеты с помощью аналитически-численного метода [1].
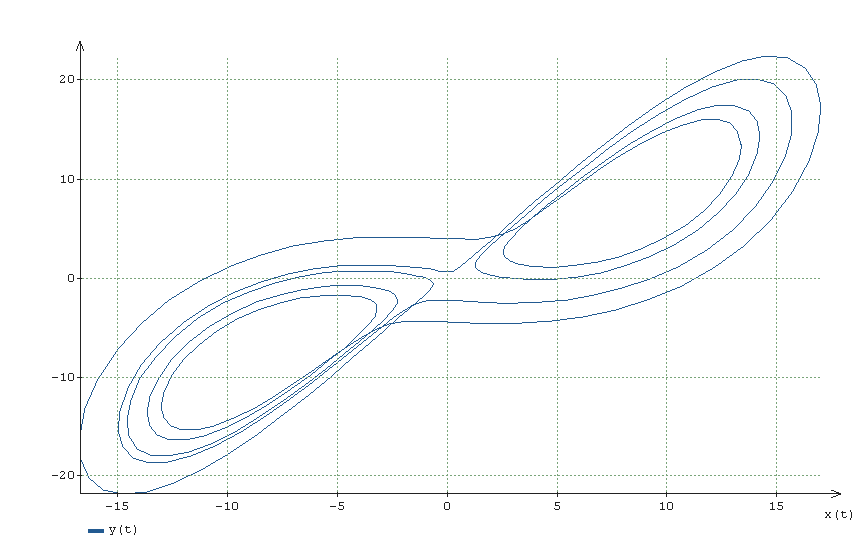
Результаты расчета на фазовой плоскости z(x):
И y(x):
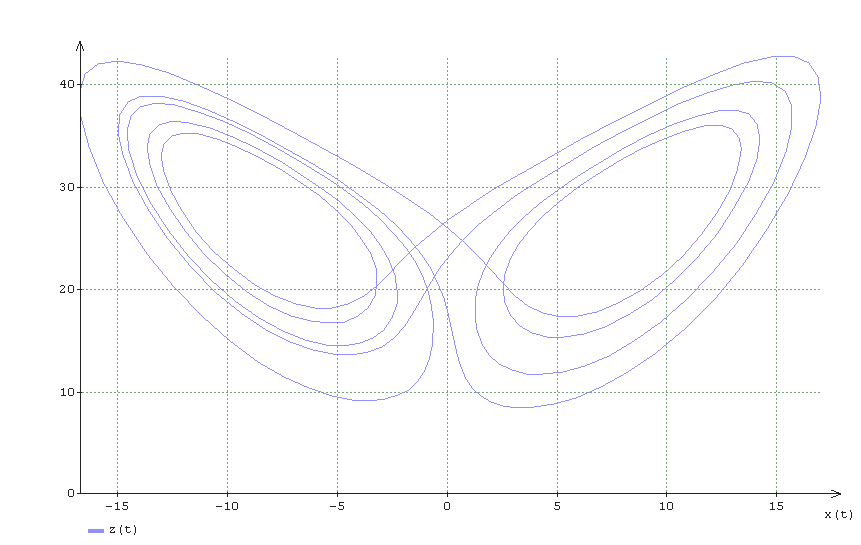
Кажется, что кривые замкнуты, но давайте рассмотрим результат поподробнее.
Применяется для решения обыкновенных нелинейных неавтономных нестационарных интегродифференциальных уравнений, описывающих динамические модели систем при детерминированных воздействиях.
При расчете регулярная составляющая искомого решения представляется в форме ряда Тейлора.
Результатом применения аналитически-численного метода при решении систем ОДУ, описывающих модель динамической системы, являются не только приближенные решения но и области, гарантированно содержащие точные решения.
То есть, кроме самого численного значения приближенного решения в результате получаются и верхние оценки предельной полной погрешности расчета на каждом шаге расчета:
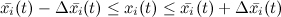
где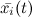 
— приближенное решение (i-я фазовая координата);
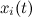— неизвестное точное решение;
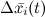— верхняя оценка предельной полной погрешности расчета приближенного решения;
Взяв параметры для расчета из статьи «Динамическая система Лоренца и вычислительный эксперимент»:
Предначальные условия, параметры динамической системы, точность математических операций — 180 знаков после запятой, точность по степенному ряду 1e-9, получим следующий результат в точке t = 6.827:
Значения производных:
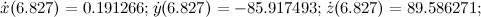
Несложно видеть, что результаты расчетов несколько отличаются от изложенных в статье.
Кроме того, если подставить результат из статьи (найденные приближенные значения решений) в исходную систему уравнений, то получим значения производных также отличающихся от указанных в статье:
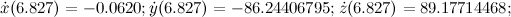
Отмечу, что повышение точности расчетов (количество учитываемых знаков после запятой и точность по степенному ряду) приводит лишь к сужению области, содержащей точные решения. Например, при задании точности 1e-55, область в точке t = 6.827 сужается до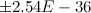 
.
Далее, я решил продолжить расчет до точки t = 12.827 и рассмотреть график результатов расчета на фазовых плоскостях z(x):
И y(x):
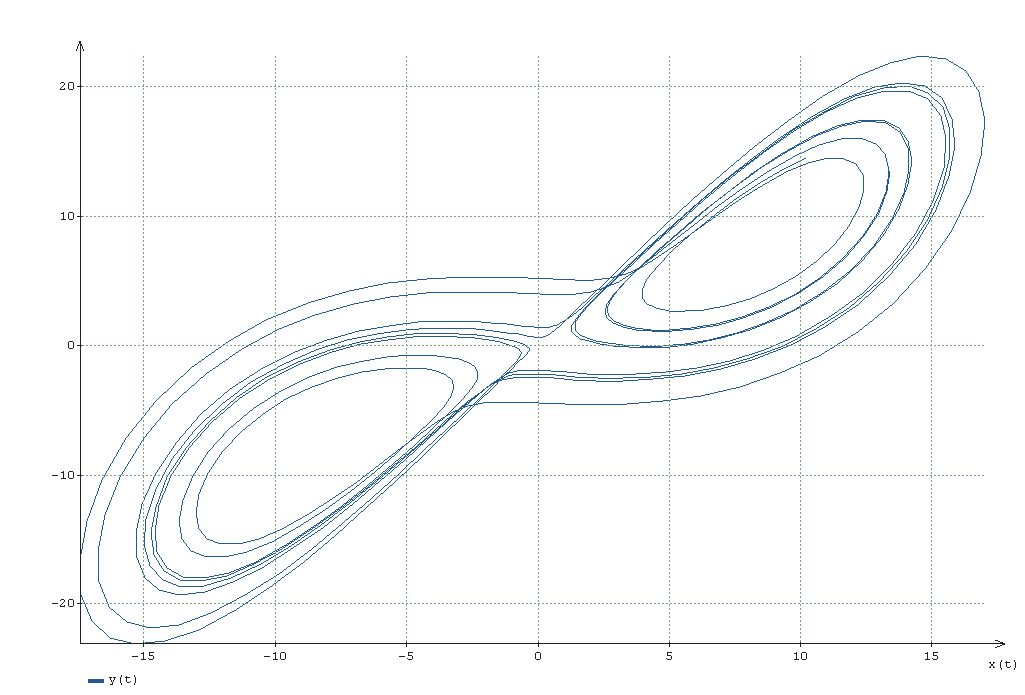
На графиках четко видно что кривые не замкнуты. Если быть еще точнее, они и на первых графиках не замкнуты, просто масштаб, в котором отображены фазовые траектории, не позволяет увидет точку разомкнутости.
Таким образом, нельзя говорить ни о каком возвращении траектории в окрестность начальной точки — об этом говорится в статье. А делать выводы на основе расчетов необходимо всегда с оглядкой на погрешность вычислений (как методическую так и вычислительную).
Литература:
1. Бычков Ю., Щербаков С. Аналитически-численный метод расчета динамических систем. — Санкт-Петербург: Энергоатомиздат,2001.
Автор: Surgun
