Цели:
Определить наиболее оптимальный алгоритм под задачи распознавания мимики человеческого лица, рассмотреть способы его реализации.
Задачи:
Провести анализ существующих алгоритмов распознавания мимики, учитывая определённые нами доминирующие признаки классификации и математической модели. На основании полученных данных выбрать оптимальный вариант алгоритма для последующей его реализации и апробации.
Введение
В предыдущих научных отчётах была разработана математическая модель распознавания мимики, и был синтезирован алгоритм распознавания мимики. Существуют два подхода в распознавании мимики – использование деформируемой модели на области губ и выхватывание векторных признаков области губ с последующим их анализом с помощью алгоритмов на основе гауссовых смесей. Для реализации распознавания мимики необходимо выбрать оптимальный алгоритм.
1. Алгоритмы распознавания человеческого лица:
1.1 Алгоритмы, основанные на деформируемой модели.
Деформируемая модель (deformable template model) – это шаблон некоторой формы (для двумерного случая — открытая либо замкнутая кривая, для трехмерного — поверхность). Наложенный на изображение, шаблон деформируется под воздействием различных сил, внутренних (определенных для каждого конкретного шаблона) и внешних (определенных изображением, на которое наложен шаблон) — модель меняет свою форму, подстраиваясь под входные данные [1]. Исходная грубая модель губ деформируется под действием силовых полей, заданных входным изображением (Рис.1).
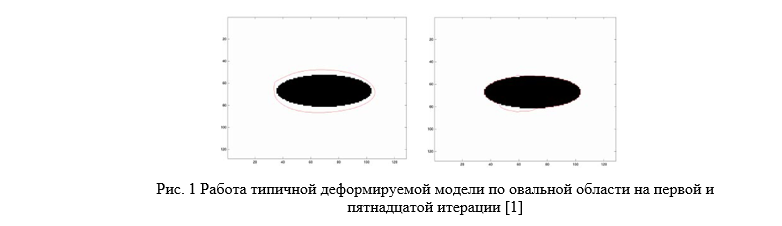
Основное преимущество над традиционными методами поиска, такими как преобразование Хафа (Hough transform [2]), в которых шаблон для поиска задается жестко, заключается в том, что деформируемые модели в процессе работы могут менять свою форму, позволяя более гибко осуществлять поиск объекта [3].
Основной недостаток деформируемых моделей [4] заключается в необходимости проведения большого числа итераций над большим количеством кадров, что значительно нагружает систему, но при вынесении основных вычислений в облако можно разгрузить систему.
Деформируемые модели можно классифицировать по типу ограничений, накладываемых на их форму, на два вида: деформируемые модели свободной формы и параметрические деформируемые модели.
1.1.1 Деформируемые модели свободной формы
Деформируемые модели свободной формы — это такие деформируемые модели, на которые накладываются лишь общие требования гладкости и непрерывности контура. Примером такой модели может служить «змея» (snake) [5]. Классическая «змея» – деформируемая модель, заданная сплайном. Изменение деформируемой модели задается перемещением контрольных точек сплайна по изображению губ, энергия задается взвешенной суммой двух составляющих: внутренней энергии (задается условиями непрерывности и гладкости контура) и внешней энергии (задается деталями на изображении, к которым притягивается «змея»). Возможно также третье слагаемое – дополнительная энергия, задающая дополнительные пользовательские ограничения. «Змеи» широко используются в обработке медицинских изображений [6], задачах отслеживания движения, сегментации [7].
Формально, «змея» – это параметрический заданный контур c(s) = (x(s),y(s)). Энергия «змеи» выражается суммой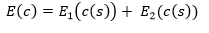 
,
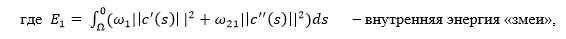
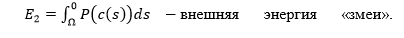Здесь P – потенциал, ассоциированный с изображением и жестко связанный с губами. Для «змеи», настроенной на поиск границ, возможно
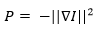, где I – яркость изображения.
Минимизируя энергию, получаем искомые параметры. Минимизация может проводиться, например, методом ветвей и границ. Для этого итеративно последовательно меняются координаты каждой из контрольных точек; изменение, которое привело к наименьшему значению энергии, используется на следующем шаге итерации. Процедура минимизации заканчивает работу, когда на очередном шаге ни одно изменение не может уменьшить энергию «змеи» (рис. 2).
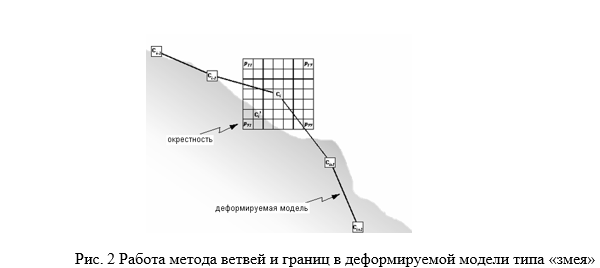
Основной недостаток «змеи» заключается в том, что если вблизи инициализирующего положения не окажется ярко выраженных деталей, влияние внутренней энергии, определяющей степень гладкости искомого объекта, имеет тенденцию чрезмерно вытягивать модель, вырождая ее в прямую, так как нулевая производная (как первая, так и вторая) прямой минимизирует энергию «змеи». Чтобы избежать этого эффекта, используют специальную разновидность деформируемых моделей, так называемый баллон (balloon) [8].
К основным преимуществам «змеи» можно отнести относительную простоту реализации (в случае не включения процедур численной оптимизации) и устойчивость к переменчивости входных данных.
В итоге можно сделать вывод о том, что использование «змеи» для распознавания мимики будет сопряжено с необходимостью использовать численные методы оптимизации, что усложнит и без того громоздкий алгоритм.
1.1.2 Параметрические деформируемые модели
Параметрические деформируемые модели — это модели, которые имеют более жесткие ограничения на форму. Модель инициализируется шаблоном строго определенной формы, и при дальнейших деформациях внутренняя энергия модели контролирует ее соответствие ограничениям по форме [9]. Такие модели получили широкое применение в распознавании лиц [10], жестов и человеческой фигуры на изображениях.
Уравнение энергии E змейки, выражающейся формулой v(s) выглядит также как и у обычной «змейки»:
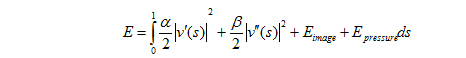
Первые два терма описывают энергию регулярности змейки. В нашей полярной координатной системе v(s) = [r(s), θ(s)], s от 0 до 1. Третье слагаемое – энергия, относящаяся к внешней силе, полученной из изображения, четвертое – с силой давления.
Внешняя сила определяется, исходя из вышеописанных характеристик. Она способна сдвинуть контрольные точки к некоторому значению интенсивности. Она вычисляется как:
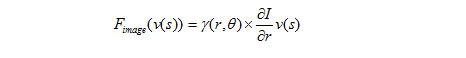
Аналитически заданные параметрические деформируемые модели описываются набором примитивов, некоторым образом связанных между собой [10]. Примитивы и связи между ними участвуют в расчете внутренней энергии, благодаря чему форма деформируемой модели не может существенно отклоняться от инициализирующей формы (Рис.3).
Другой вариант параметрических деформируемых моделей – основанные на прототипе модели (prototype based deformable models [9]). Инициализирующее положение и форма модели, основанной на прототипе, устанавливается методами машинного обучения или высокоуровневой обработкой изображения.
Преимущества параметрической модели над «змеёй» в том, что в общем случае нет необходимости в применении сдерживающих параметров, поскольку форма модели изменяется в заданных пределах. Также зачастую отбрасывается необходимость использовать численную оптимизацию т.к. исходя из экспериментальных данных [9] она работает достаточно хорошо.
Основной недостаток параметрической модели заключается в необходимости составлять обучающие выборки, и перестроении выборок в случае изменения параметров модели.
В результате сравнения «змейки» и параметрически заданной модели был сделан вывод о том, что параметрическая модель является лучшим выбором, поскольку изменение обучающих выборок более комфортно, чем изменение и настройка параметров оптимизации результатов работы «змеи».
1.2 Алгоритмы на основе гауссовых смесей.
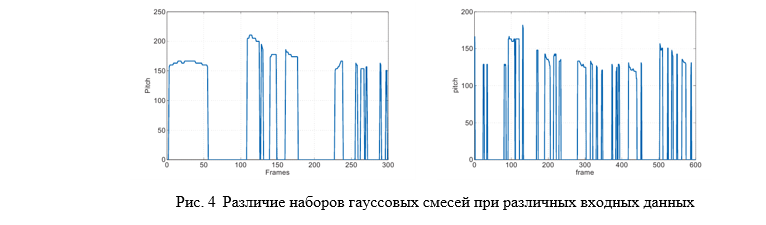
Гауссовы смеси – это совокупность распределений нормальной величины [12]. Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Сумма этих величин и даёт нам гауссову смесь (рис. 4).
Модель гауссовых смесей представляет собой взвешенную сумму M, компонент и может быть записана выражением
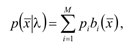(1)
где x — это D -мерный вектор случайных величин; bi(x), i = 1,...,M, — функции плотности распределения составляющих модели и pi, i = 1,..., M, — веса компонентов модели. Каждый компонент является D -мерной гауссовой функцией распределения вида
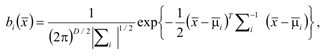(2)
Полностью модель гауссовой смеси определяется векторами математического ожидания, ковариационными матрицами и весами смесей для каждого компонента модели. Эти параметры все вместе записываются в виде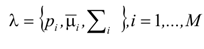
В задаче распознавания мимики каждое изображение губ представляется моделью гауссовых смесей и ставится в соответствие со своей моделью λ. Модель гауссовой смеси может иметь несколько различных форм в зависимости от вида ковариационной матрицы.
Основное преимущество использования гауссовых смесей заключается в интуитивном предположении того, что отдельные компоненты модели могут моделировать некоторое множество акустических признаков/событий [12].
Вторым преимуществом использования моделей гауссовых смесей для идентификации мимики является эмпирическое наблюдение, что линейная комбинация гауссовых распределений может представлять большое число классов изображений губ. Одна из сильных сторон смеси гауссовых моделей та, что эти модели могут очень точно аппроксимировать произвольные распределения.
Недостаток использования модели гауссовых смесей заключается в сложности извлечения вектора признаков из каждого кадра, а так же в самом анализе полученных данных, поскольку трудно разделить их на классы.
Из-за сложности реализации и большого количества вычислений использовать гауссовы смеси в задаче распознавания мимики ресурсозатратно, а из-за неоднозначности получаемых данных трудно избавится от возникающих ошибок.
Апробация и заключение:
В данном отчёте были рассмотрены алгоритмы распознавания мимики, основанные на свойствах деформируемой модели (деформируемая модель свободной формы и параметрическая модель) и статистических характеристик (алгоритмы на основе гауссовых смесей). Деформируемые модели основываются на изменении свойств исходного шаблона, а гауссовы смеси предполагают использование статистических характеристик области интереса.
Использование гауссовых смесей предполагает обработку большого количества данных [13], что ресурсозатратно, а использование параметрической деформируемой модели необходимы процедуры предобработки, занимающие как минимум 4 минуты процессорного времени [5]. Именно поэтому выбор пал на использование обычной «змеи», т.к. она наиболее оптимальна по быстродействию [3].
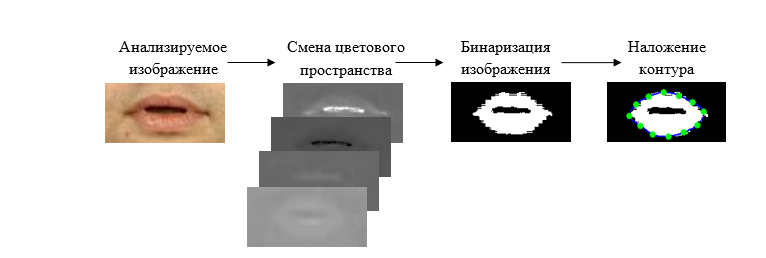
Рис. 5 Работа деформируемой модели по предварительно бинаризованному изображению губ человека.
Согласно из проведённых исследований, при предварительной бинаризации области губ удаётся в разы повысить качество работы алгоритма активного контура (рис.5). При этом удаётся избавится от процедур предварительной настройки системы и анализа эталонных изображений, как это было бы в случае использования параметрической активной модели.
Уверенное нахождение контура губ позволит в дальнейшем перейти к реализации задачи непосредственного анализа микропауз, что позволит улучшить существующие на настоящий момент системы аудио-распознаватели речи.
Список литературы
1) Demetri Terzopoulos, John Platt, Alan Barr, Kurt Fleischer. Elastically Deformable Models. Computer Graphics (Proceedings of ACM SIGGRAPH), Vol. 21, No. 4, pp. 205-214, July 1987.
2) Линда Шапиро, Джон Стокман. Компьютерное зрение. Москва: Лаборатория Базовых Знаний, 2006.
3) Michael Kass, Andrew Witkin and Demetri Terzopoulos. Snakes: Active contour models. Int. Journal of Computer Vision, Vol. 1, No. 4, pp. 321-331, January 1988.
4) Shu-Fai Wong, Kwan-Yee Kenneth Wong. Robust Image Segmentation by Texture Sensitive Snake under Low Contrast Environment. In Proc. Int. Conference on Informatics in Control, Automation and Robotics, pp.430-434, August 2004.
5) Michael Kass, Andrew Witkin and Demetri Terzopoulos. Snakes: Active contour models. Int. Journal of Computer Vision, Vol. 1, No. 4, pp. 321-331, January 1988.
6) Tim McInerney, Demetri Terzopoulos. Deformable Models in Medical Image Analysis: A Survey. Medical Image Analysis, 1(2): pp. 91-108, 1996.
7) Doug P. Perrin, Christopher E. Smith. Rethinking Classical Internal Forces for Active Contour Models. Computer Vision and Pattern Recognition, Vol. 2, pp.615-620, 2001.
8) Laurent D. Cohen. On Active Contour Models and Balloons. Computer Vision, Graphics and Image Processing: Image Understanding, Vol. 53, No. 2, pp. 211-218, March 1991.
9) Anil K. Jain, Yu Zhong, Sridan Lakshmanan. Object Matching Using Deformable Templates. IEEE Trans. on Pattern Anal. And Machine Intel. Vol. 18, No. 3, pp. 267-278, March 1996.
10) Alan L. Yuille, Peter W. Hallinan, David S. Cohen. Feature extraction from faces using deformable templates. Int. Journal of Computer Vision, Vol. 8, No. 2, pp. 99-111, August 1992.
11) Markel J.D., Oshika B.T., Gray A.H. // IEEE Trans. On Acoustics, Speech, and Signal Processing. 1977. Vol. 25. P. 330–337.
12) «Incremental Learning of Temporally-Coherent. Gaussian Mixture Models» Ognjen Arandjelovicґ, Roberto Cipolla, Department of Engineering, Cambridge.
Продолжение следует
Автор: RealSpeaker
