Наряду с политическими, социально-экономическими, организационными, военными, правовыми, специальными и информационными проблемами, решение которых предусматривается на государственном, федеральном уровне, в информационной сфере существуют проблемы математического характера, о которых в работе и пойдет речь. В работе приводятся и конкретизируются некоторые важные понятия и основные положения информационной безопасности и защиты информации. Основными нормативными документами в этой сфере являются Конституция РФ — основной закон, ФЗ О безопасности, Военная доктрина и Доктрина информационной безопасности, а также руководящие документы Федеральной службы по техническому и экспортному контролю (РД ФСТЭК)
Информационная безопасность государства — состояние защищенности его национальных интересов в информационной сфере. Информационная сфера — совокупность информационной инфрастрктуктуры страны, информации, субъектов, осуществляющих сбор, формирование, распространение и использование информации, а также системы регулирования возникающих при этом общественных отношений. Информационная сфера — системообразующий фактор жизни общества, часть социальной деятельности общества.
Целью написания работы являетя стремление автора заострить внимание читателей на первоочередных математических задачах в области информационной безопасности и защиты информации, без решения которых прогресса в ближайшие годы (возможно десятилетия) ожидать не приходится.
Описание ситуации информационного взаимодействия (воздействия)
Рассматривается группа абонентов-пользователей Г = {u1,u2,…,un}, размещенных в разных узлах сети связи или компьютерной сети, которые обмениваются сообщениями, передаваемыми по незащищенным каналам сети. Понятно, что сообщения могут содержать сведения, не предназначенные для широкой аудитории. Абоненты системы связи хотели бы иметь доступ и контакт друг с другом по мере возникновения в нем потребности, сохранения конфиденциальности их сообщений, обеспечения полного совпадения полученного на приемной стороне сообщения с тем, которое было подготовлено и отправлено передающей стороной, т.е. сохранения целостности. Кроме названных требований оба общающихся абонента не хотели бы стать участниками «гроссмейстерской атаки». Они хотели бы с высоким уровнем достоверности знать, что общаются они друг с другом, а не с подставными лицами, иметь возможность реализации взаимной аутентификации – установления подлинности отправителя получателем и наоборот. При выполнении перечисленных требований на услуги системы связи качество приема/передачи сообщения должно соответствовать заявленному.
Таким образом, достоверность, целостность, конфиденциальность, доступность должны быть обеспечены каждой паре общающихся пользователей в любой сети связи. Выполнение названных требований в сетях обеспечивается разными средствами, программно-аппаратными комплексами, реализующими достаточно сложные алгоритмы, программы, разработанные в рамках теорий электросвязи, кодирования и криптологии.
В предлагаемой работе рассматриваются основные понятия и положения криптологии, представляющей тесно взаимодействующие криптографию и криптографический анализ с примыкающей к ним стеганологией: образуемой стеганографией и стеганографическим анализом. Задачами информационного обмена, в частности, криптографии и теории кодирования являются задачи обеспечения конфиденциальности, установления подлинности абонентов и проверка целостности сообщений, обеспечение доступности субъектов к объектам и ресурсам, которая достигается распределением и разграничением доступов. Первая задача (конфеденциальность) решается применением криптографической системы (КГС), шифрованием сообщений, вторая – использованием электронной цифровой подписи (ЭЦП) и третья задача – установлением совпадения дайджестов, передаваемого и сформированного получателем. Задача обеспечения целостности решается методами теории кодов, кодированием/декодированием сообщений кодами исправляющими ошибки, корректирующими кодами. О доступности уже сказано ранее.
Общая схема реализации сеанса связи между парой абонентов (точка-точка) представлена на рисунке 1.
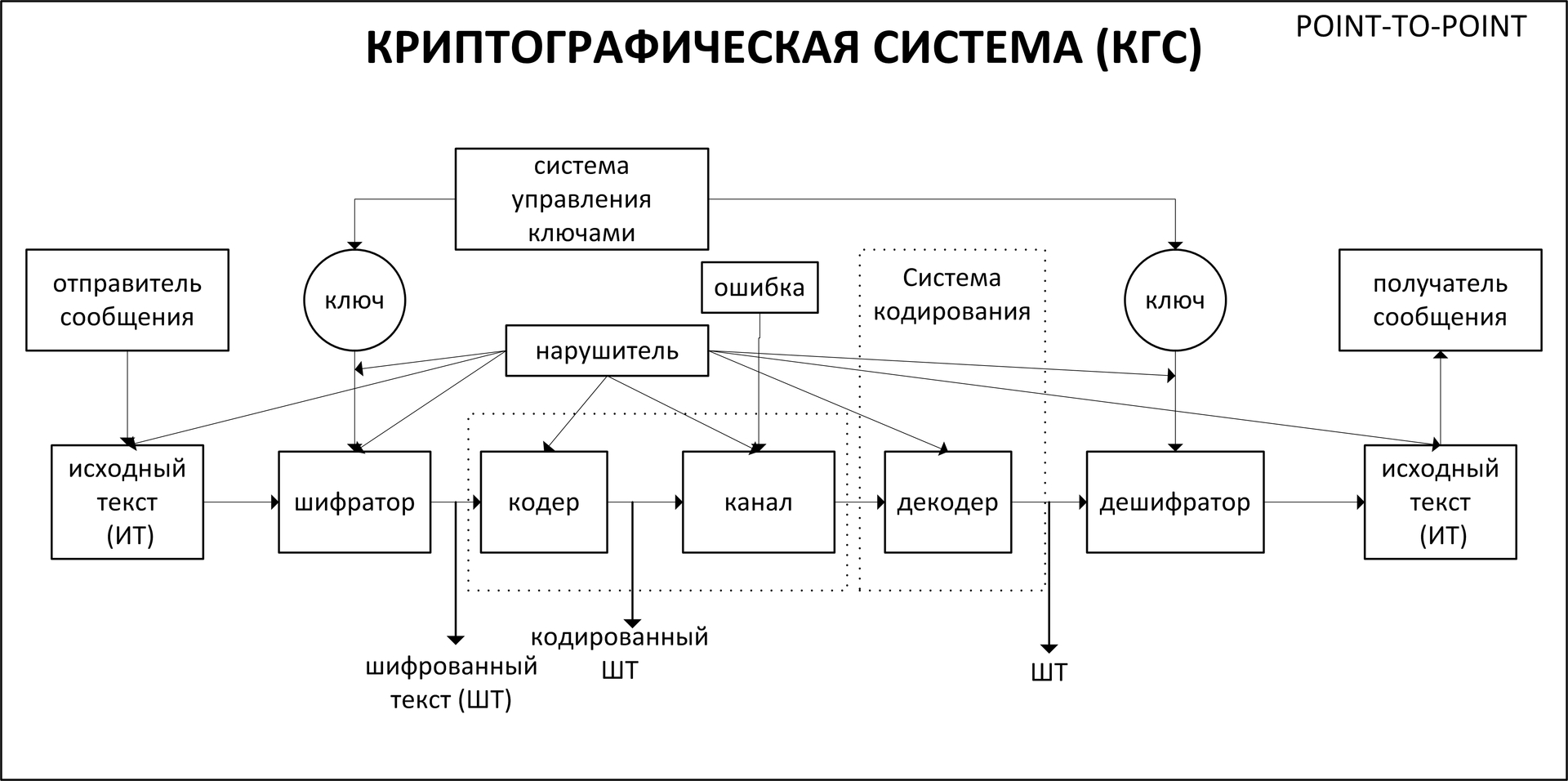
Рисунок 1 — Схема реализации сеанса связи абонентов с использованием одноключевой симметричной КГС, системы управления ключами и системы кодирования
Технология защищенного информационного обмена сообщениями
Технология информационного обмена включает субъекты, объекты, ресурсы и процессы. Субъектами являются получатель и отправитель сообщения, ресурсы (финансовые, сетевые, вычислительные, временные), объекты: источник сообщения, формирующий послание, само сообщение, ключи, вырабатываемые ключевой системой, шифрующее/дешифрующее, кодирующее/декодирующее устройство, дисплей или принтер, — то есть устройство для отображения сообщения в форму доступную для восприятия всеми субъектами получателями и отправителями.
Последовательность обработки сообщения должна быть такой как представлено на рис.1. Это связано с тем, что при наличии/отсутствии искажений шифрсообщения его дешифрование в первой ситуации с ошибками невозможно. Поэтому на стороне получателя сообщения необходимо предварительно устанавливать наличие ошибок в сообщении и внести исправления, если ошибки есть. Только после устранения ошибок возможно успешное дешифрование сообщения. Параллельно с обработкой сообщения обрабатывается цифровая подпись и выполняется ее проверка.
Одноключевая криптографическая система. Обязательными, необходимыми атрибутами сеанса связи являются идентификатор пользователя, пароль доступа и, что самое важное – ключ шифрования. В классической традиционной криптографической системе (КГС) отправитель и получатель оба используют один и тот же ключ для шифрования и дешифрования. По этой причине такие системы шифрования называют одноключевыми (симметричными). Понятно, что обе стороны должны располагать ключом до сеанса связи, т.е. ключ необходимо выработать, распределить (какую пару ключей кому) и распространить (доставить) абонентам. Это задача управления ключами. Для ее успешного решения требуется защищенный (выделенный) канал распространения ключей. Часто ключ доставлялся специальным дипкурьером. Имя одного из них Теодор Нетте широко известно и вошло в литературу и в историю.
Двухключевая криптографическая система. В 1978 году появилась публикация о новом типе КГС – двухключевой системе. Называют ее также асимметричной, системой с открытыми дверями. Отправитель и получатель сообщения используют разные ключи. По открытому ключу вычислительно очень трудно найти закрытый ключ. В этой системе каждый абонент самостоятельно формирует свою пару ключей: доступный всем отправителям открытый ключ е, которым должны пользоваться все абоненты для создания шифрсообщения, и закрытый личный ключ d получателя, который получатель хранит в тайне от всех, не разглашает его.
В таких системах отпадает необходимость в распространении ключей, что, безусловно, упрощает новую технологию защищенной связи. Но даром ничего не дается. В двухключевых системах имеются свои минусы. Шифрование в них достаточно медленный процесс. Появление подобных двухключевых систем стало возможным в связи с введением в оборот информационной безопасности нового математического объекта – односторонней функции и в множестве таких функций – функций с потайным входом (с лазейкой). Дело здесь вот в чем. Мы можем легко перемножить пару чисел р и q и получить одно число N = pq. Вычисления здесь направлены в одну сторону. Теперь допустим задано составное число N и необходимо определить его делители. Эта задача для больших чисел (10150 -10300) в настоящее время практически не решается, если нет лазейки (потайной дверцы). Такой лазейкой может быть, например, один из делителей или значение функции Эйлера от N.
В двухключевой КГС с открытым ключом получатель сообщений, который устанавливает КГС такой делитель знает, т.е. он располагает лазейкой.
Электронная цифровая подпись (ЭЦП). В цифровых подписях также используются два ключа: ключ подписи личный (не разглашаемый) и публичный (открытый) ключ проверки подписи.
Отправитель свое сообщение шифрует на открытом ключе получателя, а подписывает шифрсообщение своим закрытым ключом. Открытый ключ подписи отправителя доступен всем и получатель, используя его и проверяя цифровую подпись, убеждается, что сообщение послано и подписано этим отправителем.
Процессы в КГС. Основные процессы защищенного информационного обмена описываются в стандартах шифрования и цифровой подписи ГОСТ 28147 — 89 — для шифрования и ГОСТ 34.10 — 2012 — для ЭЦП.
При защищенном информационном обмене абонентов сообщениями реализуются следующие основные процессы. Установка КГС, выработка 4 ключей (2 для шифрования и 2 для цифровой подписи получателя), формирование сообщения, шифрование сообщения, подписание, кодирование, передача отправителем, воздействие среды и/или нарушителя, прием сообщения, декодирование, дешифрование, проверка цифровой подписи, преобразование в форму удобную для восприятия получателем. Дадим краткую характеристику процессам.
Установка КГС. Получатель А выбирает два больших простых числа рА и qА , умножает их и получает модуль шифра NА , а также вычисляет значение функции Эйлера Ф(NА ). После этого выбирает открытый ключ еА такой, что (еА , Ф(NА )) = 1, и вычисляет, используя расширенный алгоритм НОД Евклида, закрытый ключ dА , такой, что еА dА ≡1(mod Ф(NА )).
Значения (еА и NА ) и ник получателя объявляются на сетевом сервере открытыми и доступными для всех, кто будет посылать свои сообщения получателю А. Значения dА , рА , Ф(NА ), и qА сохраняются в тайне от всех. Доступ нарушителя к любой из этих величин приводит к взлому КГС.
Возможная атака на шифрсообщение. Допустим нарушителю известно Ф(NА ), и еА dА – 1 делится на Ф(NА ). Знание Ф(NА ) обеспечивает вычисление рА и qА , так как рА + qА = NА + 1 – Ф(NА ); рА – qА = [( рА + qА )2 +4Ф(NА )]0.5. Можно показать, что значения кратные функции Эйлера Ф(NА ) также достаточны для расчета рА и qА .
Отправитель В сформированное сообщение преобразует в числовую форму (двоичный вид) и разбивает его на блоки длины [ log2NА ] = mВi – блоки исходного текста. После этого находятся остатки mВiеА (modNА ) = уВi – блоки шифрсообщения, после чего отправляют их получателю А.
Получатель, располагая шифрованными блоками сообщения дешифрует их с использованием личного ключа, т.е. находит остатки уВi dА (modNА ) = mВi.
Математические проблемы информационной безопасности
Моделирование объектов (сетей локальных, корпоративных, глобальных, групп абонентов), процессов приема/передачи защищенных сообщений, информационного обмена и взаимодействия — обширная область со своими задачами и проблемами самого различного характера для приложений алгоритмов изучения и совершенствования информационной безопасности.
Проблемы защиты информационного обмена и информационной технологии находят свое отражение и в математических теориях, например, в теории чисел. Центральной проблемой настоящего времени является проблема разложения больших чисел на множители. В криптологии с ней связаны задачи криптографии, выбора ключевой информации, а в криптоанализе – с атаками на двухключевые КГС.
Такие атаки рассматриваются как со стороны нарушителей, так и со стороны криптоаналитиков своей стороны. Целью последних является выявление слабых мест алгоритмов и криптопротоколов. Обнаруженные уязвимости устраняются путем совершенствования продуктов, либо при невозможности их устранить переходят на новые более совершенные и современные средства.
Другой важной проблемой является получение простых чисел высокой разрядности и в массовых количествах. В компьютерных сетях и сетях связи обмен защищенными сообщениями требует от систем управления ключами массового изготовления простых чисел, которые выбираются из полного множества случайным образом. Ранее говорилось, что каждый абонент сети формирует для себя, по крайней мере, 4 ключа, которые он должен обновлять через определенные промежутки времени. Это означает, что потребность в простых числах существует постоянно, так как число пользователей пока только увеличивается. Мобильные телефоны сегодня имеет практически каждый житель развитых стран и большая часть жителей стран развивающихся. Системы сотовой связи охватывают все большие территории и остановки этого процесса в ближайшее время не предвидится.
Тесно к названной проблеме примыкает проблема установления простоты числа большой разрядности.
Проблема дискретного логарифма. Протокол Диффи – Хеллмана обеспечения ключами (DHDLP, 1976г). Абоненты А и В выбирают простое число р и простое g с порядком p -1 по модулю р, т.е. gp-1≡1(mod p), но gn≠1(mod p), для любого n < p -1. Абоненты А и В выбирают простые числа n< р и m < р соответственно. Затем вычисляются остатки gn(mod p), gm(mod p) и каждый из абонентов результат своих вычислений посылает другому. Далее оба вычисляют А: k ≡ gnm≡( gm)n(mod p), и В: k ≡ gnm≡( gn)m(mod p), т.е. абоненты теперь располагают одинаковыми значениями ключа, который не передавался по каналу связи через сеть и не мог быть там перехвачен. Получилась симметричная КГС.
Нарушитель может перехватить и располагать значениями gn(mod p), gm(mod p), но их использования для быстрого получения n и m или k ≡ gnm(mod p) недостаточно.
Подобная проблема дискретного логарифма сушествует и для эллиптических кривых (ЭК) над конечными полями (ЕСDLP,1985 г. Н.Коблиц, В. Миллер). На ЭК Е(Fр) появляется абелева группа, образованная точками этой кривой. Эта группа циклическая и очень большого порядка. Другими словами, при заданных двух точках ЭК Е(Fр) над полем Fp, точки Р, Q∈Е(Fр) требуется найти такое число λ (при его существовании), что Q= [λ]P.
Автор: VAE






