Решение задачи линейной регрессии с помощью быстрого преобразования Хафа

Введение

Друзья, рассмотрим нынче же задачу линейной регрессии в присутствии выбросового (некоррелированного с сигналом) шума. Эта задача часто возникает при обработке изображений (напр., при цветовой сегментации [1]), в том числе — акустических [2]. В случаях, когда координаты случайных величин можно грубо дискретизовать, а размерность задачи низка (2-3), кроме стандартных методов робастной регрессии можно воспользоваться быстрым преобразованием Хафа (БПХ) [3]. Попробуем сравнить этот последний метод по точности и устойчивости с «классическими».

Использование БПХ для линейной регрессии

Задача линейной регрессии на плоскости состоит в восстановлении линейной зависимости между двумя переменными, заданными в виде множества пар (x, y). Задавшись некоторым уровнем дискретизации координат, можно отобразить это множество на однобитном или целочисленном изображении (в первом случае мы отмечаем только факт наличия в исходных данных точки с примерно такими координатами, во втором — еще и их число). Фактически, речь идет о двумерной гистограмме исходных данных. Таким образом, неформально задача может быть сведена к поиску на изображении прямой, которая наилучшим образом описывает изображенное распределение точек.В обработке изображений в подобных случаях используется преобразование Хафа.

Преобразование Хафа является дискретным аналогом преобразования Радона и ставит в соответствие каждой прямой на изображении сумму яркостей пикселей вдоль нее (то есть одновременно вычисляет всевозможные суммы вдоль дискретных прямых). Можно ввести разумную дискретизацию прямых по сдвигам и наклонам так, чтобы параллельные дискретные прямые плотно упаковывали плоскость, а выходящие из одной точки на одном крае изображения прямые расходились по наклону на противоположном крае на целое число пикселей. Тогда таких дискретных прямых на квадрате n² будет примерно 4 * n². Для этой дискретизации существует алгоритм быстрого вычисления преобразования Хафа с ассимптотикой O(n² * log n). Этот алгоритм является близким аналогом алгоритма быстрого преобразования Фурье, хорошо параллелизуется и не требует никаких операций, кроме сложения. В работе [3] можно прочитать об этом чуть больше, кроме того, там объясняется, почему преобразование Хафа от сглаженного гауссовским фильтром изображения вообще можно применять в задаче линейной регресии. Здесь же мы продемонстрируем устойчивость этого метода.

Тестовые данные

Зададимся теперь вопросом, какое распределение мы ожидаем у входных данных. В задаче акустической локации можно считать, что у нас есть равномерно распределенные точки вдоль прямолинейного отрезка траектории движения судна, искаженные нормальным аддитивным координатным шумом. В случае же анализа цветовых кластеров распределение вдоль отрезка неизвестно и зачастую весьма причудливо. Для простоты будем рассматривать исключительно двумерное гауссово распределение с высоким эксцентриситетом. При достаточно большой дисперсии вдоль прямой и малой дисперсии в поперечном направлении свойства построенного распределения не сильно отличаются от «зашумленного отрезка».

Алгоритм генерации тестовых распределений может быть описан следующими тремя шагами:

• случайным образом выбираются «центр» и наклон (моделируется отрезок прямой);
• генерируется заданное количество точек с указанным распределением (и выбранным центром);
• добавляется однородный выбросовый шум.

Стандартное отклонение нормального распределения вдоль прямой составляло одну четвертую длины моделируемого отрезка (при таком выборе приблизительно 95% точек попадают внутрь), а длина отрезка бралась равной половине линейного размера квадратного изображения (составляющего 512 пикселей). Отношение дисперсий было равно 10.0, а количество точек распределения и доля выбросового шума варьировались. Пример подобного рода распределения изображен на рисунке 1.

Для того, чтобы сравнивать разные алгоритмы, надо уметь оценивать, насколько хорошо был найден отрезок в каждом случае. Тонкость состоит в том, что рассматриваемые алгоритмы ищут не отрезок, а прямую. Поэтому будем брать «идеальный» отрезок (A, B) и находить максимум из двух расстояний от его концов до экспериментально найденной прямой. Если обозначить через Q(L, AB) ошибку в параметрах экспериментальной прямой L, то это определение можно записать так: Q(L, AB) = max(r(L, A), r(L, B)).

Рис. 1. Образец распределения с аддитивным и выбросовым шумами. Отметками показаны концы и центр моделируемого отрезка.

Зависимость ошибки метода БПХ от размера окна сглаживания

Как было сказано выше, регрессия с использованием БПХ предполагает сглаживание. Очевидно, что размер окна сглаживания должен оказывать существенное влияние на качество работы алгоритма. Исследуем зависимость ошибки нахождения прямой от размера окна. Для каждого размера из некоторого набора была сгенерирована серия из ста изображений, затем для каждого вычислялась прямая и фиксировалась ошибка. Полученный результат представлен на рисунке 2, где ось абсцисс задает отношение сглаживающего параметра s_H к стандартному отклонению нормальной («поперечной») сотставляющей координатного шума s_L. Точками на рисунке обозначаются средние ошибки, а вверх и вниз от них откладываются среднеквадратичные отклонения. Можно заметить, что результат является наилучшим в случае, когда s_H близко к s_L, т.е. когда размер окна не сильно отличается от «толщины» отрезка.

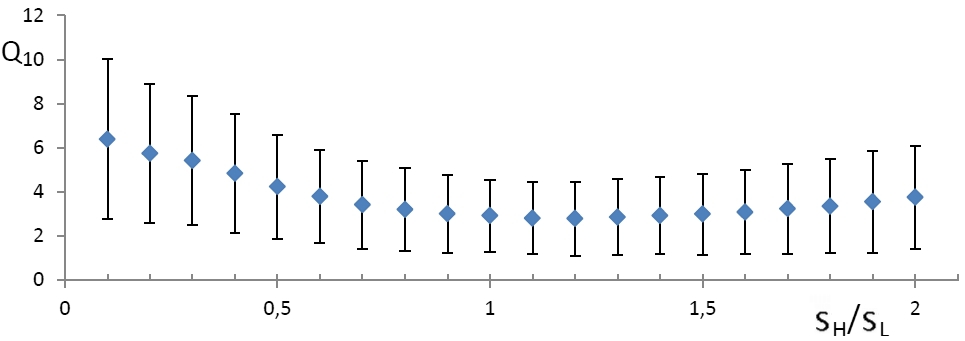Рис. 2. Зависимость ошибки метода Хафа от размера окна сглаживания.

Сравнение с МНК и его робастными модификациями

Самым очевидным, хотя и неправильным (в нашем случае) методом линейной регресии является, конечно же, метод наименьших квадратов (МНК), который для ортогональной регрессии совпадает с методом главных компонент (англ. PCA). В свое время для случая выбросового шума его допилили до «МНК с итеративным пересчетом весов», причем во все учебники вошли варианты с весовой функцией Хьюбера и биквадратной весовой функцией [4].

Сравним метод БПХ с простым МНК, а также с МНК с пересчетом весов с обеими весовыми функциями. Параметры функций возьмем, как рекомендуют теоретики: k_H = 1.345 для Хьюбера и k_B = 4.685 для биквадратной функции.

На рисунке 3 видно, как средняя ошибка каждого из четырех методов зависит от плотности выбросового шума µ – отношения количества выбросовых шумовых точек к общему числу пикселей на изображении (плотность выбросового шума отложена по оси абсцисс, а средняя ошибка метода представлена на оси ординат). Каждый замер проводился на ста различных сгенерированных изображениях. Из рисунка очевидно, что метод, основанный на применении БПХ, оказался самым устойчивым к добавлению выбросового шума, хотя при малом количестве выбросовых точек он уступает другим методам в точности. К тому же, этот метод оказывется более стабильным, то есть реже ошибается катастрофически (вверх и вниз от каждой точки на рисунке отложена четверть среднеквадратичного отклонения ошибки).

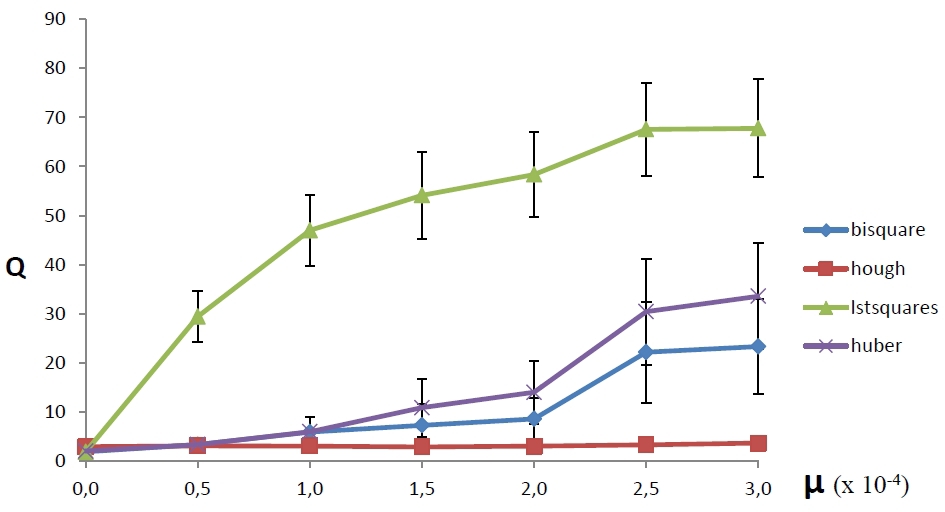Рис. 3. Зависимость средней ошибки от плотности выбросового шума у БПХ и МНК-методов.

Сравнение с медианными методами

Удивительно, но про по-настоящему хорошие методы робастной регрессии редко рассказывают в ВУЗ-ах. Но мы-то с вами, дорогой читатель, знаем про волшебный метод Тейла-Сена [5], и потому ограничиться сравнением с робастным МНК было бы бесчестно. В классическом алгоритме Тейла-Сена наклон прямой вычисляется как медиана среди наклонов прямых, проведенных через все пары точек выборки. Помимо этого используется модифицированный вариант, в котором сначала для каждой точки распределения выбиралась медиана наклонов всех прямых, проходящих через эту и какую-либо другую точку распределения, после чего из полученных значений выбиралась медиана («медиана медиан»). В обоих случаях для определения параметра сдвига прямой берется медиана среди значений {y_i — m x_i}, где m – найденный описанными способами угловой коэффициент прямой.

На рисунке 4 показано сравнение теперь уже с этими методами. В рамках каждой серии по-прежнему проводилось сто экспериментов, обозначения тоже не изменились. Видно, что в рассмотренном интервале плотности выбросового шума средняя ошибка метода БПХ является наименьшей и не растет, в то время как методы Тейла-Сена имеют пропорциональный рост ошибки. Также видно, что метод БПХ по-прежнему имеет наименьший разброс ошибки.

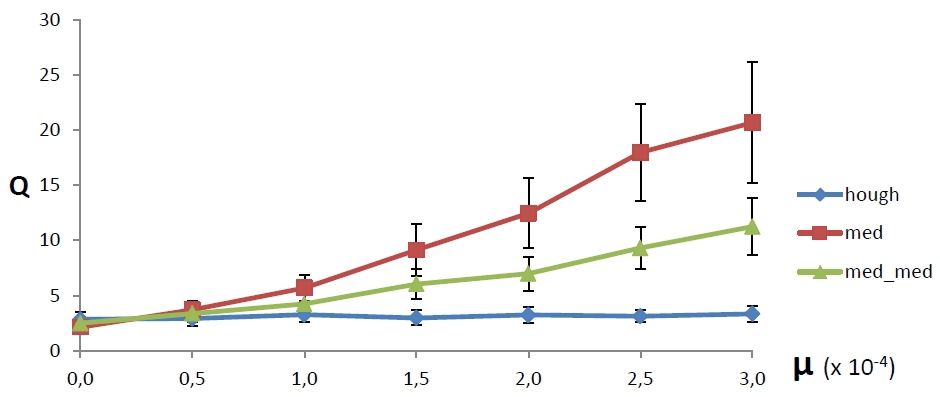Рис. 4. Зависимость средней ошибки от плотности выбросового шума у БПХ и медианных методов.

Сравнение методов при наличии структурированного шума

Отдельный интерес представляет случай, когда выбросовый шум имеет собственную пространственную структуру. Для примера добавим к уже рассмотренным видам шумов некоррелированную с сигналом шумовую компоненту с круговым двумерным нормальным распределением. Пример комбинации всех трех видов шумов приведен на рисунке 5. Прямой показан идеальный ответ.

Рис. 5. Пример отрезка, зашумленного аддитивным, а также равномерным и структурированным выбросовыми шумами.

Посмотрим теперь на зависимость ошибки от плотности «круглого» структурированного шума при фиксированных параметрах выбросового и аддитивного шумов. По-прежнему для каждого значения плотности сгенерировано сто изображений. Результаты приведены на рисунке 6. Заметно, что методы разделились на три группы, причем удивительным образом классические робастные методы мало отличаются от МНК. Видно, что «срыв» у всех МНК-методов происходит практически сразу, медианные методов стабильно работают при гораздо больших загрязнениях данных, но тоже рано или поздно перестают работать, в то время как у метода БПХ резкого срыва не наблюдается вовсе.

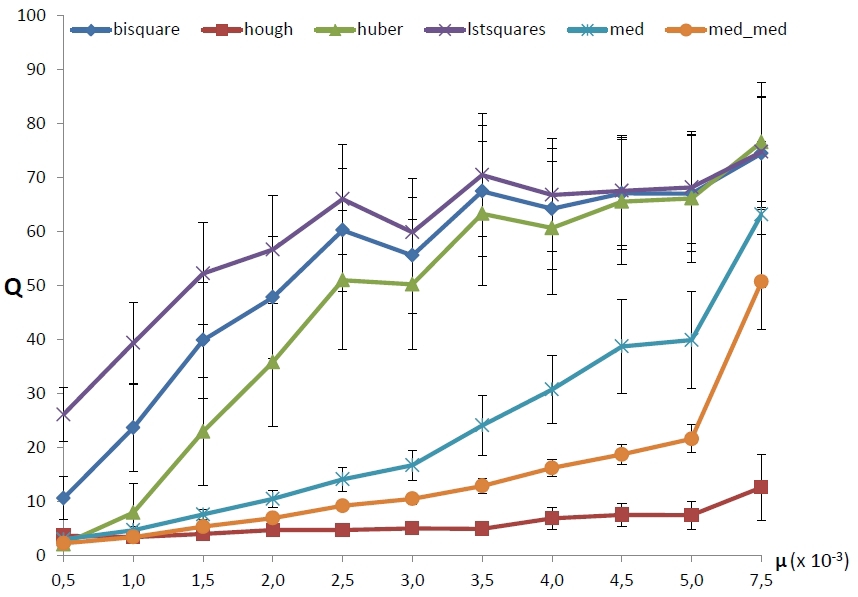Рис. 6. Зависимость средней ошибки от плотности структурированного шума.

Обсуждение

Решение задачи линейной регрессии с помощью комбинации гауссового сглаживания и преобразования Хафа является устойчивым к одновременно присутствующим аддитивному координатному и выбросовому шумам. Сравнение с другими распространенными робастными методами показало, что предложенный алгоритм является более устойчивым, когда плотность выбросового шума достаточно высока. Следует отметить при этом, что метод применим только в маломерном случае (алгоритм БПХ может быть обобщен на любую размерность, но объем памяти, необходимый для кодирования задачи в виде изображения размерности выше трех — пугает). Кроме того, даже в двумерном случае использование БПХ будет невыгодным, если точек мало, а требуемая относительная координатная точность высока. Это связано с тем, что у остальных методов вычислительная сложность зависит от числа точек, а у БПХ — от числа дискрет пространства. Впрочем, при малом числе точек возможно вычисление преобразования Хафа «грубой силой». Казалось бы, так не выйдет, поскольку предварительно мы хотим сгладить изображение, однако еще Израилю Моисеевичу Гельфанду было известно, что гауссово сглаживание в определенном смысле перестановочно с преобразованием Радона. Используя этот трюк, ассимптотику метода в приближении малого числа точек можно улучшить до O(n²), однако n по-прежнему обозначает линейный размер изображения, так что почти наверняка это все равно слишком плохо. Зато при большом числе точек метод БПХ кроет все остальные методы как бык — овцу. Такие дела.

Литература

[1] D.P. Nikolaev, P.P. Nikolayev Linear color segmentation and its implementation, Computer Vision and Image Understanding. 2004, V.94 (Special issue on colour for image indexing and retrieval), pp. 115-139
[2] L. Nolle. Application of computational intelligence for target tracking. In Proc. of 21st European Conference on Modelling and Simulation, 2007, pp. 289-293.
[3] D.P. Nikolaev, S.M. Karpenko, I.P. Nikolaev, P.P. Nikolaev. Hough transform: Underestimated Tool in Computer Vision Field. In Proc. of 22nd European Conference on Modelling and Simulation, 2008, pp. 238-243.
[4] P.J. Rousseeuw, A.M. Leroy. Robust Regression and Outlier Detection. Wiley series in probability and statistics, 2003.
[5] Wilcox, R. Rand. Theil–Sen Estimator, Introduction to Robust Estimation and Hypothesis Testing, Academic Press, 2005, pp. 423–427.

Автор:

Источник