Всем добрый день! Этот короткий пост посвящен рассмотрению моделей процессов разработки Waterfall и Agile (на примере Scrum и/или Kanban). И вот в чем дело: с точки зрения заказчика, процесс не столь важен, сколько срок и бюджет удовлетворительного с точки зрения функционала результата. И если известно, что (изменения не учитываются) затраты Waterfall-процесса идут по S-кривой, а затраты Agile-процесса накапливаются линейно (так как ресурсы используются одновременно все), то как они должны различаться по эффективности. Чтобы исследовать этот вопрос, необходимо построить модели и сравнить их, и для этого будет использована несложная математика.
| Совет №30: Считайте везде, где это возможно. Если счет невозможен — вычисляйте. Используйте оценки, полученные на основании одного лишь экспертного суждения, только лишь в крайнем случае. Макконнел С. Сколько стоит программный проект (2007). |
Предыстория
Управление проектом, условно, можно разделить на две составляющие — на планирование и управление ходом.
С этой точки зрения для waterfall всё ясно — составили пошаговый (аналитика-разработка-тестирование) календарный план задач по оценкам сроков, распределили задачи и вперед реализовывать.
Со Scrum и Kanban ненамного сложнее: последовательность планирования осуществляется через приоритеты в backlog, разработка контролируется либо через burndown chart для всего проекта (в Scrum), либо с помощью lead time (в Kanban). Оценка сложности задач влечет за собой и оценку сроков — через тройку итераций или задач становится ясной скорость, на основе которой можно давать оценку даты окончания.
В данном посте ход проекта моделироваться не будет (это вообще себе вполне отдельная задача), а будет сравниваться эффективность плановая.
«На кончике пера»
План представим как две составляющие:
- Суммарное количество единиц (аналог storypoints) сложности задач на весь продукт проекта (P),
- Количество привлекаемого в момент t персонала n(t) <= N (равенство в случае Agile).
Далее, обозначим как r — время на реализацию одной единицы сложности задачи одним специалистом, c — стоимость одного специалиста за единицу времени, T назовем суммарное время проекта, S — его бюджет, p=p(t) — количество выполненной работы на момент времени t.
Тогда для Agile мы имеем, что за единицу времени мы выполним столько работы, сколько N человек выполняют за раз единиц задачи:
p'A(t) = N / r => (зная, что вначале выполненной работы нет) pA(t) = N * t / r.
Откуда, собственно, ясно следующее:
TA = r * P / N; SA(t) = c * N * t; SA = c * r * P.
На этом пока с Agile закончим, к счастью модель его плана оказалась (в моей версии) достаточно проста. Всё становится сложнее с Waterfall-планом, так как в нём привлекаются специалисты по ходу проекта. При этом, однако, остается основное соотношение:
p'(t) = n(t) / r.
Всё дело в выборе функции n(t). Мы знаем, что в нуле она ноль, и в конце проекта — ноль. Больше мы ничего не знаем. Далее будем предполагать, что она симметричная, достигает в середине значения N, и растет квадратично (я выбрал квадратичную функцию из тех соображений, что это простейший вариант при заданных условиях).
n(t) = N * 4 * (T — t) * t / T2.
Зная, что p(0) = 0, можно выписать интеграл p'(t):
p(t) = 2 * N * t^2 / (r * T) — 4 * N * t^3 / (3 * r * T^2) => T = 3 * P * r / (2 * N).
О! А вот это уже интересно! При выбранном законе привлечения команды к проекту по времени, длина проекта вырастает в полтора раза! А ведь ситуация с привлечением не всего персонала сразу типична для Waterfall.
Что у нас со стоимостью? Её также можно найти интергированием (по t).
s'(t) = c * n(t) => s(t) = 2 * c * N * t^2 * (3 * T — 2 * t) / (3 * T^2),
откуда
SW = 2 * c * N * T / 3 = c * P * r.
Бюджет тот же.
Кривые
Убедимся, что мы получили S-кривую на отрезке [0; T]. Подставим значения с = 1, r = 2, P = 100, N = 100 и получим T = 30.
График p = p(t) для Waterfall:
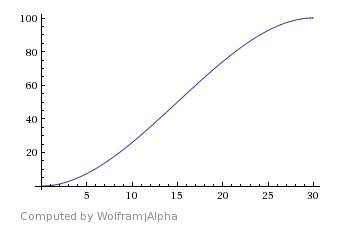
График s = s(t) для Waterfall:
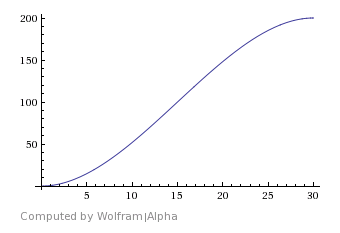
Немного выводов
Кто-то сочтет данный пост капитанством, и будет недалек от истины. Ведь конечно, модели слегка «людоедские», и не учитывают изменения (которые, в сущности, являются обновлениями планов). В то же время, если собирать различное количество человек на Waterfall и Agile, сроки можно будет сравнять, но бюджеты будут различны.
Я не буду говорить, что Agile оптимален (несмотря на то, что это максимум по срокам при таком моделировании) — слишком много упрощений в моделях. Но вполне возможно, что рассмотренная механика объясняет некоторую разницу между эффектами при различных подходах, и кто-то возьмет на вооружение рассмотренный принцип для оптимизации своих проектных планов: привлекать как можно большее количество человек к решению задач сразу — может снизить срок при сохранении бюджета (хотя и может казаться, что бюджет увеличится).
Автор: S_A