Первая мысль, которая посещает голову человека, столкнувшегося с проблемой планирования — это придумать собственную умную эвристику решения задачи маршрутизации.
Ну, ведь и правда. Пришел заказчик (а чаще привели), описал свою задачу, свои специфичные для бизнеса условия. Тут же приходит мысль, как решать именно его задачу, бороться с проблемами его бизнеса. В итоге анализ его данных и условий рождает собственный эвристический алгоритм, заточенный на эти условия.
Бывает и наоборот, сначала посетила мысль об умной эвристике, а уже потом нашли заказчика или нишу бизнеса, где этим алгоритмом решается задача.
Процесс разработки эвристики на простом примере
Итак, снова представим себя логистами маленькой такой компании из первой статьи. В ней мы с вами поняли, что полный перебор не катит эффективен. Мощные (квантовые и даже «живые») компьютеры будущего или целые кластеры современных компьютеров в облаке могут решать задачи планирования больших размерностей точными методами. Однако стоимость вложения в их развитие и невозможность на данный момент продавать продукт как сервис заставляет разрабатывать «умные» эвристические алгоритмы. К тому же самый простой и легкий эвристический алгоритм «ближайшего соседа» в большинстве случаев получает решение на 30-50% хуже оптимального. А из-за жадности в некоторых случаях получает наибольший путь. Поэтому очевидно необходимо разработать «умный» эвристический алгоритм.
Планирование на бумаге
Алгоритм «ближайшего соседа» получает самый длинный путь, если клиенты размещены ромбом. В этом случае мы платим дорого за возврат обратно по длинному пути. Тогда чтобы избежать ромбов, посмотрим, как размещены на карте наши клиенты.

Попробуем вручную на бумаге сами составить оптимальный тур.
Распечатали карту. Вооружились карандашами. Далее, опираясь на нашу интуицию, нанесли на карту маршруты движения транспортных средств от исходного пункта к пунктам назначения и обратно. Каждый из нас составил свой путь вручную за 5 минут. Маршруты у нас получились разные. Оказалось, трудно определить «на глаз», какой из них оптимальнее по расстоянию. Измерим длину линейкой. Сравнив свои маршруты с полученным алгоритмом «ближайшего соседа» стало понятно, что мы составили лучше. Если цель составить хорошее расписание, то тут можно и остановиться. Ведь для данного примера любые изменения расположения точек и появление новых потребует лишь еще 5 минут времени логиста. Ручное планирование всегда будет актуально. И во многих маленьких компаниях так и поступают.
Однако в реальной жизни есть большие компании (либо логисты обслуживают сразу несколько маленьких компаний). Или существует много различных ограничений, которые на бумаге или в excel просто так уже не учтешь. Для таких случаев необходимо автоматическое планирование. Вот тут и возникает необходимость составить алгоритм наших действий, то есть объяснить машине наше интуитивное планирование. Однако составить алгоритм с учетом всех интуитивно понятных вещей является совершенно нетривиальной задачей.
Как же мы думали?
Сели вместе с подругой и думаем, как выразить наше интуитивное планирование в алгоритме.
Ну, без карты то точно никуда, хорошо, что сели и посмотрели на расположение клиентов.
Она говорит: «Я увидела, что в правом нижнем углу от депо большое скопление клиентов».
«Угу, а остальные разбросаны вокруг малыми группами и далеко друг от друга» — добавляю я.
Далее, мы выяснили, что соединяли точки внутри малых групп очевидным способом, а в большой группе в уме пробовали переставлять несколько точек местами с учетом нескольких шагов вперед, чтобы в итоге соединить с другой группой минимальной дугой.
Формализуем алгоритм
Можно учесть, что основные перестановки будут в нижнем правом квадрате, а вставка остальных точек между ними будет только увеличивать общее расстояние, значит лучше просто отбросить одиночные точки и попереставлять только те, что в правом нижнем квадрате. Точек для перестановок получится 17.
17! = 355687428096000
Сможем посчитать полным перебором?
Core i5-2500K 3.3 ГГц ~ 100 Гфлопс, т.е. 1011 операций в секунду.
355687428096000 / 1011 / 60 = 59 секунд
Сможем, но если бы там было даже на 1 точку больше, то потребовалось бы уже 17 минут (помним опыт вычислений).
Хорошо бы еще разбить точки на более маленькие квадраты. Скажем, по 5 точек в квадрате.
Ну давайте разделим квадрат с 17 точками еще на 4 квадрата. Если точек больше 5 в квадрате, то его делим на 4 квадрата. И так далее до тех пор, пока точек в квадрате будет не больше 5.
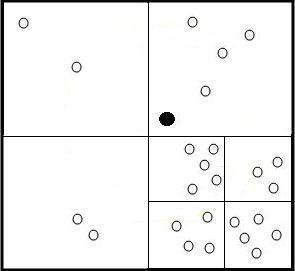
Однако здесь для простого примера представлен вариант, основанный на оригинальной эвристике, но отличающийся от нее. В оригинале эвристика используется для определения ближайших машин к заказу, а не для составления маршрута.
Мы не сможем объяснить машине, как переставлять точки с учетом нескольких шагов вперед. Так как мы уже разделили задачу на квадраты и теперь в алгоритме доступен только этот квадрат. К тому же следующий квадрат еще не обсчитан и алгоритм на данном шаге не знает, какая точка из другого квадрата будет соединяться с этим квадратом. Интуитивно в уме мы можем примерно прикинуть, какой будет маршрут в другом квадрате, машина же не может «прикинуть».
Поэтому далее в каждом квадрате используем полный перебор для нахождения точного пути.
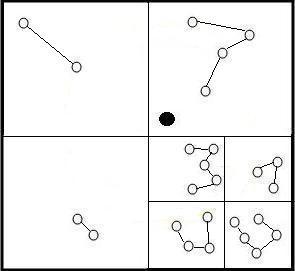
Теперь соединим пути в квадратах с ближайшими точками других квадратов.
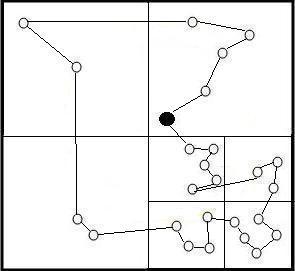
Получился формализованный алгоритм, работающий немного дольше алгоритма «ближайшего соседа», но получающий более близкий к оптимальному путь.
Немного проанализировали и получили свой «умный» эвристический алгоритм!
Однако и это решение не оптимальное. В ближайшем к депо малом квадрате путь можно уменьшить, если соединить нижние точки по-другому. На этапе построения пути в малом квадрате алгоритм об этом ничего не знает. Только на текущем этапе, после построения маршрута в целом, мы можем сообщить алгоритму правила при которых надо перестроить соединение групп, но и эти правила не охватят все интуитивные мысли, которые нас посетили сразу при построении на бумаге. А формализацию описанных выше правил тоже можно провести недостаточно, что приведет к не оптимальности в другом месте, например в другом квадрате. Получается алгоритм можно улучшить, главное сообщить как-то ему об этом.
Все меняется...
«А что если наши клиенты со временем будут меняться и уже не будет такой картины на карте?» — говорит второй логист.
«Надо тестировать алгоритм на разных данных» — отвечаю я.
А что если так?
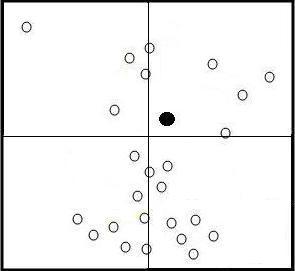
Далее пошли долгие и тяжелые споры, о том, как генерировать данные для теста, с чем сравнивать расстояние (пока только с «ближайшим соседом»), насколько полученное расстояние больше чем оптимальное, можно ли получить оптимальное расстояние и т.д. и т.п.
Возможно, вообще надо будет придумывать какой-то новый алгоритм для новых данных, которые сгруппированы иначе.
Вывод
Разработка новых собственных «умных» эвристических алгоритмов не только возможна, но и необходима. Однако собственные алгоритмы, зачастую, заточены на определенный набор данных, заказчика или малую нишу бизнеса и качество таких алгоритмов трудно оценить.
Автор: Glonassova






