Иногда чисто теоретические, математические абстракции находят удивительное соответствие в живой природе. Пожалуй, самые известные среди них — фракталы. Но вот группе математиков, физиков и химиков из США, Южной Кореи и Японии удалось найти ещё один замечательный пример. Они доказали, что известная теорема о четырёх красках в точности описывает структуру некоторых кристаллов.
Теорема о четырёх красках утверждает, что всякую расположенную на сфере или на плоскости карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Много лет картографы использовали эту теорему для подготовки географических карт. Однако, в последние десятилетия она представляет больший интерес не столько для картографов, сколько для математиков, из-за сложности доказательства. Её удалось доказать только в 1976 году, спустя 124 года после того, как теорему сформулировали в 1852 году. Говорят, что это первая крупная математическая теорема, доказанная с помощью компьютера. Судя по всему, до сих пор не предложено её доказательства без использования компьютера.
Возвращаясь к находке междисциплинарной группы учёных, они изучали свойства кристалла FexTaS2. Это слоистая структура, принадлежащая к классу дихалькогенидов переходных металлов (TMD), такую можно обнаружить под микроскопом в сплавах металлов и магнитах. Именно слоистая структура TMD определяет физические макросвойства, например, стали. В FexTaS2 тонкие слои TaS2 чередуются с ионами Fe, образуя массивную кристаллическую решётку.
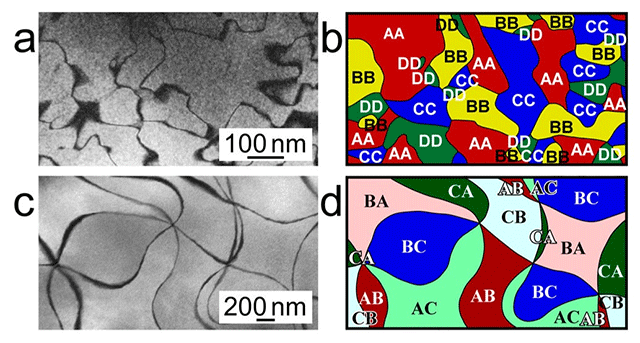
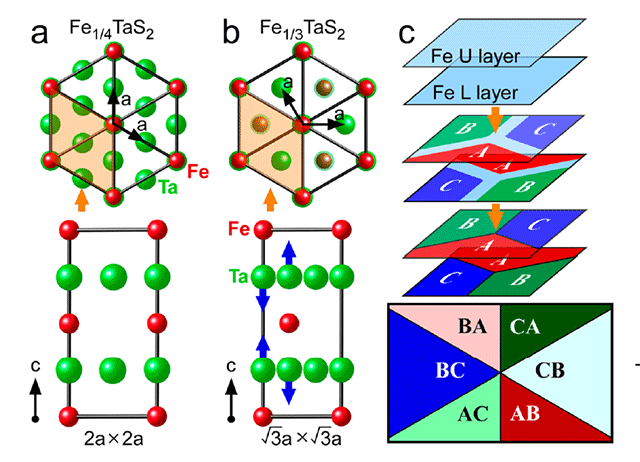
Учёные изучили свойства двух разных типов решётки с разным количеством ионов железа, входящих в структуру: для x = 1/4 и 1/3. Выяснилось, что две эти решётки демонстрируют совсем разные физические свойства: кристаллы отличаются и по размеру узлов, и по последовательности слоёв, и по количеству видов слоёв в решётке. В случае с Fe1/4TaS2 в решётке оказались слои четырёх видов, а в случае Fe1/3TaS2 — шести видов. Авторы исследования пришли к выводу, что кристаллическая решётка подчиняется математическим условиям. В первом случае это теорема о четырёх красках, а во втором — 6-валентный граф.
В любом случае, каждый узел в кристаллической решётке никогда не соприкасается с узлом такого же типа, а только с другими узлами, как и в случае с красками на географической карте.
Для 6-валентного графа кристаллическую решётку можно «раскрасить» в два прохода: сначала двумя (например, тёмный и светлый), а затем тремя цветами (например, красный, зелёный и синий, как на иллюстрации). В таком расположении по соседству никогда не появляются участки одного цвета, причём учитываются и первая, и вторая характеристика. То есть светло-красный не может соседствовать с тёмно-красным или любым другим светлым.
Конечно, никто не раскрашивает кристаллы, но именно теорема о красках позволяет интуитивно понять логику, по которой сформирована физическая структура. Если понять, как формируются свойства, можно создать новые материалы, которые найдут применение в электронике, оптике и многих других областях.
Автор: alizar






