Профессор Джим Белк (Jim Belk) показал, что программа Mathematica полезна не только в науке, но и в повседневной жизни. По просьбе одного любителя бильярда профессор рассчитал траекторию шаров при разбиении ударом битка идеально по центру пирамиды.
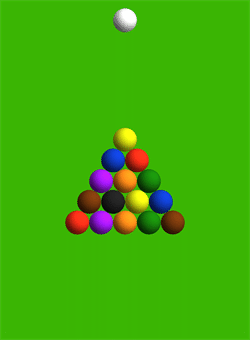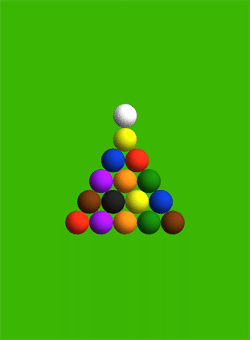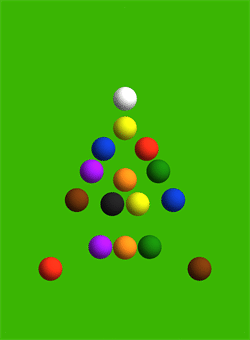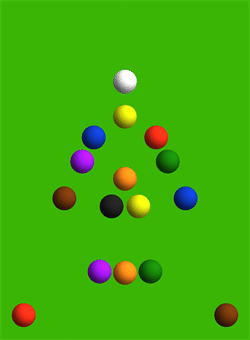
Траектории установлены с помощью численных дифференциальных уравнений.
модели численных дифференциальных уравнений.
При этом приняты некоторые допущения:
* все шары считаются идеально упругими и почти идеально жёсткими;
* каждый шар имеет массу в 1 единицу и радиус в 1 единицу;
* биток двигается со скоростью 10 единиц в секунду;
* взаимодействие между двумя шарами описывается формулой

где d — расстояние между центрами шаров,
Формула составлена исходя из законов механики контактного взаимодействия.
По этой модели, все взаимодействия между шарами укладываются в 0,2 миллисекунды и ни один шар не сжимается при ударе сильнее, чем на 0,025% своего радиуса.
На иллюстрации показаны силы взаимодействия между каждой парой соударяющихся шаров. Что интересно, непосредственно в процессе соударения всей пирамиды шары практически не двигаются.
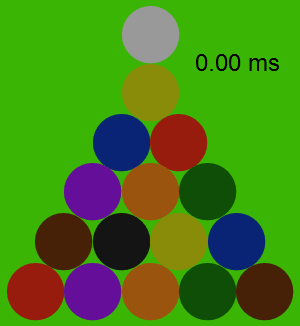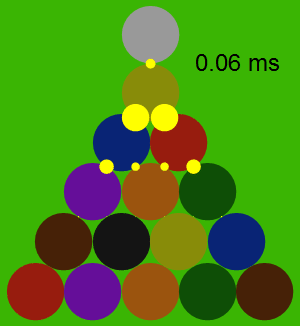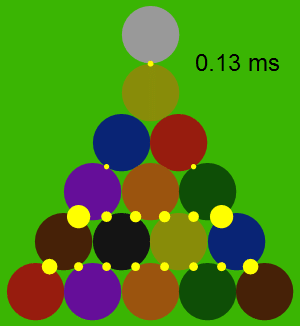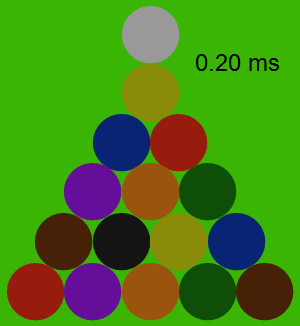
Профессор рассчитал направление и скорость движения каждого из 15 шаров пирамиды, а также битка. В соответствии с расчетом, сильнее всего должны отлетать угловые шары 11 и 15: их начальная скорость составляет 5,6 единиц в секунду, то есть 56% от скорости битка. Медленнее всего двигается шар № 5 в самом центре пирамиды: скорость 0,12 единиц в секунду.
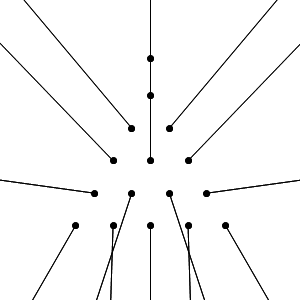
Скорость и направление каждого шара указано в таблице.

Автор: alizar


